Вычисление избыточных элементов

f ₀ = = = α³, f ₁ = = = α, f ₂ = = = 1,

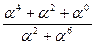f ₃ = = = α³.

Итак, искомая кодовая комбинация кода Рида-Соломона (7,3) имеет вид

f(x)=α³+α¹x+α⁰x²+α³x³+x⁴, что в точности соответствует порождающему многочлену кода.

Задачи

1. Построить кодирующее устройство для укороченного циклического кода (10,5) с 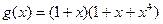и проследить по тактам процесс формирования избыточных элементов для какой-либо комбинации. Результат проверить алгебраически.

2. Построить устройство обнаружения ошибок (схему вычисления синдрома) для укороченного (10,5) – кода с .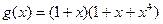

3. С помощью схемы вычисления синдрома предыдущей задачи определить принадлежность комбинаций и 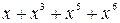коду (10,5).

4. Построить кодирующее устройство для кода (15,5) с .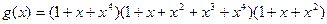

5. Построить генератор последовательности длины 7 и получить эту последовательность.

6. Построить кодирующее устройство для кода Рида-Соломона (7,5) на основе схемы рис 6.10.

7. Построить генератор элементов поля GF(2⁴)

8. Построить генератор элементов поля GF(2⁵)

9. Закодировать α⁰ = 1 (элемент поля GF(2³)) кодом Рида-Соломона (7,5), используя процедуру быстрого декодирования.

10.Построить проверочную и порождающую матрицы кода Рида-Соломона (7,5) с помощью схемы деления на порождающий многочлен g(x)=α³+α¹x+α⁰x²+α³x³+x⁴.

Дата добавления: 2015-08-02