Читайте также:
|
Для получения информации о погрешности интерполирования необходимо оценить разность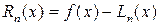 
, считая функцию 
достаточно гладкой. Можно получить [5]:
(7.10.3)
где 
- точка, в которой 
, причем 
, 
- некоторая постоянная, которая выбирается так, чтобы в некоторой точке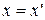 
, не совпадающей ни с одним из узлов интерполяции 
, функция 
обратилась в нуль. Подробнее см. [5].
Формула (7.10.3) позволяет оценить погрешность полиномиальной интерполяции, если известна оценка для производной 
. Полагая
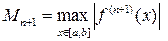, (7.10.4)
имеем
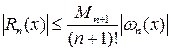. (7.10.5)
Дата добавления: 2015-08-03; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интерполяционный многочлен Лагранжа | | | Квадратурные формулы Ньютона-Котеса |