|
Читайте также: |
Пусть необходимо вычислить интеграл 
на отрезке 
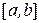. Разобьем интервал на 
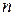частей узлами 
. Функцию 
заменим интерполяционным многочленом
, (7.10.6)
где 
оценивается по формуле (7.10.3). Тогда имеем
, (7.10.7)
где 
- погрешность интегрирования. Из (7.10.5) следует, что
. (7.10.8)
Подставляя (7.10.1) в (7.10.7), получим
, (7.10.9)
где
(7.10.10)
- коэффициенты квадратурной формулы. Формулы (7.10.9) называют формулами Ньютона-Котеса. Рассмотрим частные случаи.
Дата добавления: 2015-08-03; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Погрешность интерполирования | | | Формула трапеций |