Поскольку истинное значение Xи неизвестно, погрешность находят по приближенной формуле

Δ ≈ X – X_д, (6.2)

где X_д – действительное значение измеряемой величины, заведомо более точное, чем X. {1К7}

Относительной погрешностью δ результата измерения называют отношение абсолютной погрешности Δ к значениям X_д или X, выраженное в долях или процентах:

, (6.3)

или

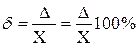. (6.4)

В зависимости от источника возникновения погрешности результата измерения различают инструментальную Δ_и, методическую Δ_мет и субъективную Δ_суб составляющие этой погрешности:

Δ = Δ_и + Δ_мет + Δ_суб. (6.5)

Инструментальнаяпогрешность обусловлена погрешностями применяемых средств измерений, методическая – несовершенством метода измерений, а субъективная – индивидуальными особенностями оператора. Пример методической погрешности (погрешности метода измерений): погрешность, вызванная изменением измеряемой физической величины при подключении средства измерений к объекту (погрешность от взаимодействия средства измерений с объектом). Пример субъективной погрешности: погрешность отсчитывания по шкале прибора. {1К8}

Если в процессе измерения физической величины она не изменяется (статическое измерение), то имеет место статическая погрешность результата измерения. В противном случае возникает дополнительная составляющая погрешности, называемая динамической погрешностью результата измерения.

При многократном измерении не изменяющейся во времени физической величины результаты измерений изменяются, причем эти изменения в общем случае нельзя предсказать. Поэтому результат измерения X и погрешность результата измерения Δ следует считать случайными величинами. Математическое ожидание называют систематической погрешностью Δ_с:

Δ_с = . (6.6)

Тогда

Δ = Δ_с + 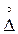, (6.7)

где 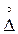- составляющая погрешности Δ, имеющая нулевое математическое ожидание; ее называют случайной (или центрированной) погрешностью. {1К9}

Основными характеристиками погрешности Δ являются: функция распределения F (Δ), плотность вероятности f (Δ), математическое ожидание = Δ_с и среднеквадратическое отклонение σ(Δ) = σ. {1К10}

{1К10}

По определению F (Δ) – вероятность того, что погрешность не превышает значения Δ,

,

,

,

,

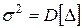где D [Δ] – дисперсия погрешности.

Функция распределения может быть выражена через плотность вероятности:

.

Дата добавления: 2015-08-02