
Читайте также:
|
Задача 4-а. Имеется собрание сочинений из 6 томов некоего автора. На верхней полке умещаются только 4 тома. Эти 4 тома берут из 6 томов случайным образом и расставляют на верхней полке случайным порядком. Какова вероятность того, что тома расположатся в порядке 1, 2, 3, 4 или 4, 3, 2, 1?
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Обозначить все события, указанные в задаче. | Событие В - тома расположатся в порядке 1, 2, 3, 4 или 4, 3, 2, 1. | |
| Вычислить число n всех равновозможных исходов. | Число всех равновозможных исходов есть размещение,
равное n =  = 360. = 360.
| |
| Вычислить число всех исходов m, благоприятствующих событию А. | Количество всех исходов m, благоприятствующих событию А, есть размещение m =2, т.к. в условии указаны лишь два возможных варианта. | |
Найти формулу вероятности для данного случая, пользуясь
классическим определением вероятности по формуле 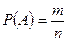 . .
| Пользуясь классическим определением по формуле 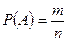 , имеем
P(B)= , имеем
P(B)=  . .
|
Задача 4-б. Имеется собрание сочинений из 6 томов некоего автора. На верхней полке умещаются только 4 тома. Эти 4 тома берут из 6 томов случайным образом и расставляют на верхней полке. Какова вероятность того, что для размещения на верхней полке будут выбраны тома 1, 2, 3, 4?
Решение:
| № п/п | Алгоритмы | Конкретное соответствие данной ситуации предложенному алгоритму |
| 1. | Обозначить все события, указанные в задаче. | Событие В – «для размещения на верхней полке будут выбраны тома 1, 2, 3, 4». |
| 2. | Вычислить число n всех равновозможных исходов. | Количество всех равновозможных исходов есть сочетание (т.к. порядок расположения томов не важен), равное
n =  =15. =15.
|
| 3. | Вычислить число всех исходов m, благоприятствующих событию А. | Количество всех исходов m, благоприятствующих событию А равно m =1, т.к. возможен единственный вариант. |
| 4. | Найти формулу вероятности для данного случая, пользуясь
классическим определением вероятности по формуле 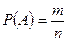 . .
| Пользуясь классическим определением по формуле 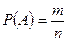 , имеем P(B) = , имеем P(B) =  . .
|
Задача 4-в. Из партии в 20 деталей, среди которых 6 дефектных, наугад берут 3 детали. Найти вероятность того, что одна из трех деталей с дефектом.
Решение
| № п/п | Алгоритмы | Конкретное соответствие данной ситуации предложенному алгоритму |
| Обозначить все события, указанные в задаче. | Событие А - одна деталь с дефектом. | |
| Вычислить число n всех равновозможных исходов. | Число всех равновозможных исходов – есть сочетание (порядок не важен):

| |
| Вычислить число всех исходов m, благоприятствующих событию А. | Т.к. в условии задачи сказано, что только одна из трех деталей с дефектом, значит две другие без дефекта. Поэтому количество всех исходов m, благоприятствующих событию А, есть произведение сочетаний (порядок не важен): 
| |
Найти формулу вероятности для данного случая, пользуясь
классическим определением вероятности по формуле гипергеометрических распределений:
 . .
| Пользуясь классическим определением по формуле 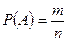 , имеем формулу числа успехов гипергеометрических распределений. Тогда , имеем формулу числа успехов гипергеометрических распределений. Тогда  . .
|
Алгоритм на умение № 5
Дата добавления: 2015-07-25; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление вероятности событий по определению | | | Задача № 5. |