
Читайте также:
|
разделу 3 «Элементы математической статистики»
1/18. Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты.
2/19. Построение полигона и гистограммы
3/20. Вычисление точечной оценок параметров распределения по выборке.
4/21. Вычисление точечной несмещенной оценки для дисперсии.
5/22. Нахождение с помощью статистических таблиц интервала, в который с заданной вероятностью попадает случайная величина, распределенная нормально или по Стьюденту.
6/23. Вычисление доверительных интервалов для математического ожидания m нормального распределения.
7/24. Вычисление доверительного интервала для генеральной дисперсии D и среднеквадратичного отклонения s.
8/25. Вычисление доверительного интервала для вероятности р наступления события А с помощью таблиц нормального распределения.
Комплексные умения и алгоритмы
к разделу 1 «Основные понятия и теоремы теории вероятностей»
| № | Умения | Алгоритмы |
| Вычисление числа соединений - вариантов различных подмножеств (выборок) для конечных множеств. | 1.Установить количество элементов всего множества n и количество элементов его подмножества m.
2. Определить, влияет ли порядок расположения элементов в подмножестве на число вариантов различных подмножеств, состоящих из этих m элементов.
3. Выбрать, в зависимости от конкретного случая, комбинаторную операцию:
а) если число комбинаций всего множества зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то перестановки без повторений Pn=n!;
б) если число комбинаций всего множества зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то перестановки с повторениями 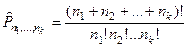 ;
в) если число комбинаций в подмножестве (выборке) зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то размещения без повторений ;
в) если число комбинаций в подмножестве (выборке) зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то размещения без повторений 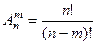 ;
г) если число комбинаций в подмножестве (выборке) зависит от порядка расположения элементов в нем и элементы повторяются, то размещения с повторениями ;
г) если число комбинаций в подмножестве (выборке) зависит от порядка расположения элементов в нем и элементы повторяются, то размещения с повторениями 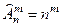 ;
д) если число комбинаций в подмножестве (выборке) не зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то сочетания без повторений ;
д) если число комбинаций в подмножестве (выборке) не зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то сочетания без повторений 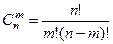 ;
е) если число комбинаций в подмножестве (выборке) не зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то сочетания с повторениями ;
е) если число комбинаций в подмножестве (выборке) не зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то сочетания с повторениями 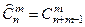 . .
| |
| Вычисление вероятностей событий по определению. | 1.Ввести обозначения для заданных величин и вопроса задачи.
2. Выбрать формулу вероятности, соответствующую данному случаю:
а) классическое определение: если задано общее число равновозможных исходов n и число исходов m, благоприятных событию А (которые можно сосчитать), то находим вероятность по формуле 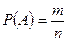 ;
б) геометрическое определение: если все возможные исходы можно изобразить с помощью геометрической фигуры (отрезок, круг, полоса, куб и др.– как полное пространство элементарных событий W), то надо
- нарисовать эту фигуру, соответствующую полному пространству элементарных исходов W;
- внутри нее нарисовать фигуру, соответствующую исходам, благоприятствующим событию А,
- вычислить площади фигур А и W,
- найти вероятность как отношение этих площадей по формуле P(A) ;
б) геометрическое определение: если все возможные исходы можно изобразить с помощью геометрической фигуры (отрезок, круг, полоса, куб и др.– как полное пространство элементарных событий W), то надо
- нарисовать эту фигуру, соответствующую полному пространству элементарных исходов W;
- внутри нее нарисовать фигуру, соответствующую исходам, благоприятствующим событию А,
- вычислить площади фигур А и W,
- найти вероятность как отношение этих площадей по формуле P(A) 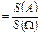 . .
| |
| Вычисление вероятностей событий по известным вероятностям других событий, с ними связанных. | 1. Обозначить все события, указанные в задаче. Известные вероятности представить в виде дроби.
2.Установить связи между событиями.
3. Вычислить требуемые вероятности, используя теоремы сложения и умножения вероятностей, а также формулу для вычисления противоположного события;
если надо вычислить вероятность того, что событие произойдет
а) не менее, чем k раз, то надо найти P(m ³ k)= 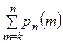 ;
б) если «хотя бы один раз» или «не менее одного раза» -
P(0< m £ n)= ;
б) если «хотя бы один раз» или «не менее одного раза» -
P(0< m £ n)= 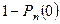 (событие, противоположное тому, что A не произошло ни разу),
если «хотя бы 2 раза» - Pn(2 £ m £ n)= (событие, противоположное тому, что A не произошло ни разу),
если «хотя бы 2 раза» - Pn(2 £ m £ n)= 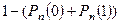 ;
в)не более чем k раз, то вычисляют ;
в)не более чем k раз, то вычисляют 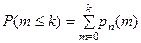 ;
г)более, чем k раз, то вычисляют ;
г)более, чем k раз, то вычисляют 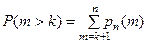 ;
д) менее, чем k раз, то вычисляют ;
д) менее, чем k раз, то вычисляют 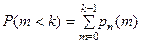 ; ;
| |
| Вычисление вероятностей событий в зависимости от числа различных подмножеств конечных множеств (различных соединений). | 1. Обозначить все события, указанные в задаче.
2. Вычислить число равновозможных исходов n и число исходов m, благоприятствующих событию А, пользуясь комбинаторными операциями по алгоритму 1, а также правилами суммы и произведения.
3. Найти формулу вероятности для данного случая, пользуясь
классическим определением по формуле 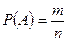 . .
| |
| Вычисление вероятности события A по формуле полной вероятности. Вычисление вероятности одной из гипотез по формуле Байеса. | 1.Дать описание всех гипотез H 1, H 2, …, Hn, на которые можно разбить пространство элементарных исходов и события A.
2.Вычислить вероятность каждой гипотезы P (H 1), P (H 2),…, P (Hn).
3. Вычислить условную вероятность события A по каждой гипотезе P (A / H 1), P (A / H 2),..., P (A / Hn).
4. Вычислить вероятность события A по формуле полной вероятности: 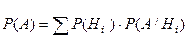 .
5.Вычислить вероятность гипотезы Hi при условии, что событие А произошло, по формуле Байеса: .
5.Вычислить вероятность гипотезы Hi при условии, что событие А произошло, по формуле Байеса:
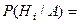 = = 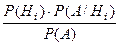 . .
| |
| Вычисление вероятностей числа m успехов в n независимых повторных испытаниях (биномиальные распределения), по формуле Бернулли, если надо найти точное значение m, где n<10. | 1. Ввести обозначения для заданных величин: числа испытаний, числа успехов, вероятности наступления события A, и выписать их значения. Выписать формулу для искомой вероятности, придерживаясь общепринятых обозначений:
- n - число испытаний при n <10,
- m - число успехов наступлений события A,
- p - вероятность наступления события A в единичном испытании,
- q = 1 - p (вероятность неудачи),
- Pn (m) - вероятность наступления события A m раз в n испытаниях.
В колонке "Конкретное соответствие" выписать заданные в задаче значения n, m и p.
2. Сосчитать вероятность:
если требуется найти вероятность того, что событие произошло
а) ровно m раз, то надо пользоваться формулой Бернулли для биномиальных распределений:
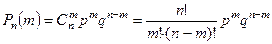 б) не менее, чем k раз, то надо найти P(m ³ k)=
б) не менее, чем k раз, то надо найти P(m ³ k)= 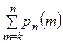 ; по алгоритмам 3а) и 5а).
в) если «хотя бы один раз» или «не менее одного раза»-
P(0< m £ n)= ; по алгоритмам 3а) и 5а).
в) если «хотя бы один раз» или «не менее одного раза»-
P(0< m £ n)= 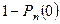 (событие, противоположное тому, что A не произошло ни разу),
г)хотя бы 2 раза - Pn (2 £ m £n)= (событие, противоположное тому, что A не произошло ни разу),
г)хотя бы 2 раза - Pn (2 £ m £n)= 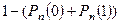 и т.д., по алгоритмам 3-б) и 5-а). и т.д., по алгоритмам 3-б) и 5-а).
| |
| Вычисление вероятностей числа m успехов в независимых повторных испытаниях n (биномиальные распределения), по формуле Пуассона, если вероятность р наступления события А мала, а n велико и l =nр<10; | 1. Ввести обозначения для заданных величин, используя алгоритм 5.
2. Вычислить вероятность по формуле Пуассона
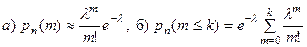 , используя для вычислений таблицы 1-а(конкретные значения) и 1-б (значения на интервале), а также алгоритмы 3а) и 3б).
Вычисления можно выполнить на калькуляторе. , используя для вычислений таблицы 1-а(конкретные значения) и 1-б (значения на интервале), а также алгоритмы 3а) и 3б).
Вычисления можно выполнить на калькуляторе.
| |
| Вычисление вероятностей для числа m успехов в n независимых повторных испытаниях, если n велико и np>10, когда надо найти для m а) конкретное значение вероятности; б)вероятность попадания в интервал [m1,m2]. . | 1.Ввести обозначения для заданных величин, используя алгоритм 5.
2. а) Вычислить вероятность, используя формулу Муавра-Лапласа: 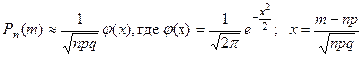 , функция j(х) затабулирована (таблица 2),
затабулирована причем j(х)=j(-х).
б) Вычислить вероятность, используя интегральную формулу Лапласа: Рn(m1£m£m2)=Ф(х2)-Ф(х1), где , функция j(х) затабулирована (таблица 2),
затабулирована причем j(х)=j(-х).
б) Вычислить вероятность, используя интегральную формулу Лапласа: Рn(m1£m£m2)=Ф(х2)-Ф(х1), где
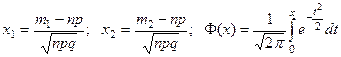 и
Ф(х) - функция Лапласа затабулирована (таблица 3), причем Ф(-х)=-Ф(х). и
Ф(х) - функция Лапласа затабулирована (таблица 3), причем Ф(-х)=-Ф(х).
|
Алгоритм на умение № 1
Вычисление числа соединений - вариантов различных подмножеств (выборок) для конечных множеств
Задача1-а. В футбольном турнире участвовали команды пяти факультетов. Найти число вариантов возможного распределения мест между ними.
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Установить количество элементов всего множества n и количество элементов его подмножества m. | Множество состоит из пяти элементов n=5, подмножество в условии не рассматривается. |
| 2. | Определить, влияет ли порядок расположения элементов в подмножестве на число вариантов различных подмножеств | В задаче требуется найти различные варианты распределения мест между командами, т.е. порядок расположения элементов важен |
| 3. | Выбрать, в зависимости от конкретного случая, комбинаторную операцию: а) если число комбинаций всего множества зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то использовать формулу перестановок без повторений Pn=n!; | Т.к. число комбинаций всего множества зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то выбираем формулу перестановок без повторений Pn=n! Имеем: P5=5!=120 вариантов. |
Задача 1-б.Найти число вариантов распределения призовых мест на футбольном турнире между пятью командами нашего факультета.
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Установить количество элементов всего множества n и количество элементов его подмножества m. | Множество состоит из пяти элементов n=5, подмножество призовых мест m=3. |
| 2. | Определить, влияет ли порядок расположения элементов в подмножестве на число вариантов различных подмножеств, состоящих из этих m элементов. | В задаче требуется найти различные варианты распределения призовых мест между командами, т.е. порядок расположения элементов в подмножестве призовых мест важен. |
| 3. | Выбрать, в зависимости от конкретного случая, комбинаторную операцию:
в) если число комбинаций в подмножестве (выборке) зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то использовать формулу размещений без повторений 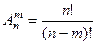 . .
| Т.к. число комбинаций в подмножестве зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то выбираем формулу размещений без повторений 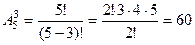 вариантов.
вариантов.
|
Задача 1-в. Сколько игр будет проведено в футбольном турнире на первенство факультета по футболу, если в нем участвуют пять команд и каждая играет с каждым из соперников по одной игре?
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Установить количество элементов всего множества n и количество элементов его подмножества m. | Множество состоит из пяти элементов n =5, подмножество команд, участвующих в одной игре состоит из двух элементов (два противника), т.е. m =2. |
| 2. | Определить, влияет ли порядок расположения элементов в подмножестве на число вариантов различных подмножеств, состоящих из этих m элементов. | В задаче требуется найти различные варианты составления плана проведения такого турнира, но порядок расположения элементов в подмножестве не важен (два противника на каждой игре равноправны). |
| 3. | Выбрать, в зависимости от конкретного случая, комбинаторную операцию:
д) если число комбинаций в подмножестве (выборке) не зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то использовать формулу сочетаний без повторений 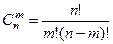 . .
| Т.к. число комбинаций в подмножестве не зависит от порядка расположения элементов в нем и нет повторяющихся элементов, то выбираем формулу сочетаний без повторений 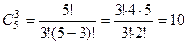 вариантов.
вариантов.
|
Задача 1-г. На футбольном турнире каждой команде присваивается число – двоичный номер, состоящий из цифр 1(победа) и 0(поражение), заработанных в каждой проведенной игре. Найти число возможных двоичных номеров этого турнира между пятью командами факультета.
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Установить количество элементов всего множества n и количество элементов его подмножества m. | Множество «мест» для записи двоичного числа состоит из двух элементов n =2, «подмножество» мест для записи результатов игр (победа или поражение) m =10. |
| 2. | Определить, влияет ли порядок расположения элементов в подмножестве на число вариантов различных подмножеств, состоящих из этих m элементов. | В задаче требуется найти различные варианты распределения нулей и единиц между командами, т.е. порядок расположения элементов в подмножестве важен. |
| 3. | Выбрать, в зависимости от конкретного случая, комбинаторную операцию:
в) если число комбинаций в подмножестве (выборке) зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то использовать формулу размещений с повторениями 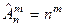 . .
| Т.к. число комбинаций в подмножестве зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то выбираем формулу размещений с повторениями 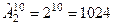 варианта.
Замечание.
Эту задачу можно было решить, пользуясь лишь правилом произведения: на каждом из возможных десяти мест, предназначенных для записи результата игры может быть одна из двух цифр – и 1, и 0. Поэтому количество цифр 2 необходимо умножить десять раз по числу проведенных игр, т.е. варианта.
Замечание.
Эту задачу можно было решить, пользуясь лишь правилом произведения: на каждом из возможных десяти мест, предназначенных для записи результата игры может быть одна из двух цифр – и 1, и 0. Поэтому количество цифр 2 необходимо умножить десять раз по числу проведенных игр, т.е. 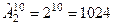 варианта. варианта.
|
Задача 1-д. Сколько различных слов можно составить из букв слова «барабан»?
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Установить количество элементов всего множества n и количество элементов его подмножества m. | Множество состоит из семи элементов n =7, подмножество в условии не рассматривается. |
| 2. | Определить, влияет ли порядок расположения элементов в подмножестве на число вариантов различных подмножеств | В задаче требуется найти различные варианты распределения данных букв между семью местами, для них предназначенными, т.е. порядок расположения элементов важен. |
| 3. | Выбрать, в зависимости от конкретного случая, комбинаторную операцию:
а) если число комбинаций всего множества зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то использовать формулу перестановок с повторениями 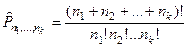
| Т.к. число комбинаций всего множества зависит от порядка расположения элементов в нем и есть повторяющиеся элементы, то выбираем формулу перестановок с повторениями.
Сосчитаем число повторяющихся букв:
n 1=3 (для буквы а), n 2=2 (для буквы б), n 3= n 4=1 (для букв р и н), т.е. 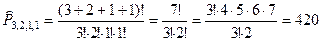 вариантов.
вариантов.
|
Алгоритм на умение № 2
Дата добавления: 2015-07-25; просмотров: 214 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приложение 3 Алгоритмы решения ключевых задач | | | Вычисление вероятности событий по определению |