
Читайте также:
|
(геометрические распределения)
Задача № 10. Вероятность того, что образец бетона выдержит нормативную нагрузку, равна 0.9. Случайная величина X – число возможных испытаний до появления первого бракованного образца. Составить ряд распределения, найти функцию распределения ДСВ X, построить её график и найти все числовые характеристики (ограничиться тремя-пятью испытаниями).
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму | |||||
| 1. | Ввести обозначения для заданных величин | n – число испытаний
p – вероятность выдержать испытание
p =0.9, q =1- p =0.1,
Найти 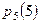 , , 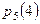 , , 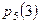 , , 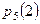 , , 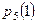 , , 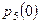
| |||||
| 2. | Сосчитать требуемую вероятность, выбрав соответствующую содержанию задачи формулу | Т.к. случайная величина X -число возможных испытаний до появления первого бракованного образца, то воспользуемся геометрической вероятностью:
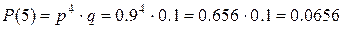 и т.д. и т.д.
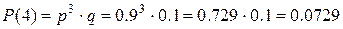
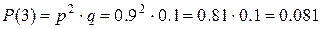
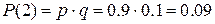
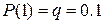
| |||||
Найти числовые характеристики ДСВ по формулам М (х)= 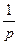 D (x)=
D (x)= 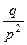
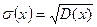
| М (х)= 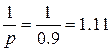 ,
D (x)= ,
D (x)= 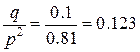 , ,
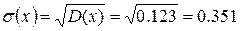 . .
| ||||||
| Составить ряд распределений случайной величины X – числа возможных образцов | |||||||
| x | |||||||
| P | 0.1 | 0.09 | 0.0081 | 0.0729 | 0.0656 | ||
| Составить функцию распределения случайной величины X – числа возможных образцов и построить график. | 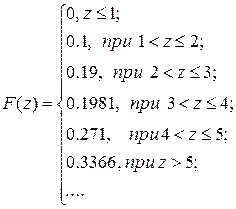
|
Алгоритм 11
Дата добавления: 2015-07-25; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли. | | | Успехов гипергеометрических распределений |