Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Бернулли

Приложение 3 Алгоритмы решения ключевых задач | III. Комплексные умения и алгоритмы к | Вычисление вероятности событий по определению | Вычисление вероятностей событий с помощью соединений | Задача № 8 | Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли. | Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании | Успехов гипергеометрических распределений | Распределенной на отрезке [a,b], а также вероятность | Вычисление числовых характеристик НСВ, имеющей |


Читайте также:
  1. Say these numbers in English. (Назовите числа по-английски.)
  2. V. Порядок проведения государственной итоговой аттестации для выпускников из числа лиц с ограниченными возможностями здоровья
  3. А) показателем 3-го лица единственного числа глагола в Present Indefinite;
  4. А) показателем 3-го лица единственного числа глагола в Present Indefinite;
  5. А) показателем 3-го лица единственного числа глагола в Present Indefinite;
  6. Аналитический метод определения перемещений в балке при изгибе. Дифференциальное уравнение упругой линии. Вычисление прогибов и углов поворотов сечений.
  7. Арифметические операции с отрицательными числами

Задача № 6. Вероятность того, что отремонтированный телевизор выдержит нормативную нагрузку, равна 0.9. Найти вероятность того, что из 7 телевизоров, находящихся в ремонте, испытания выдержат: а) ровно 5; б) не менее 5; в) хотя бы один; г) не более 5.

Решение:

№ Алгоритмы Конкретное соответствие задания заданному алгоритму
  Ввести обозначение для заданных величин n – число испытаний m – число телевизоров, выдержавших испытания р – вероятность выдержать испытания р = 0.9; q = 1 – р = 0.1; n = 7.Найти а) р 7(5); б) р 7 (m £ 5 £ 7)
  Сосчитать требуемую вероятность по формуле Бернулли 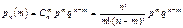Так как n < 10, нужно воспользоваться формулой Бернулли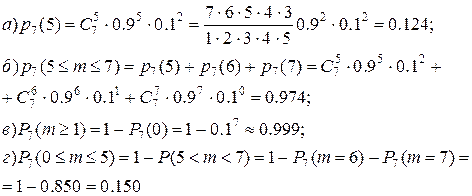

 

 

Алгоритм №7

Дата добавления: 2015-07-25; просмотров: 190 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Задача № 5.| Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона
mybiblioteka.su - 2015-2024 год. (0.005 сек.)