
Читайте также:
|
Задача № 2-а. Студент знает ответы на 18 вопросов зачета из 30. Какова вероятность того, что он вытащит на зачете известный ему вопрос?
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Ввести обозначения для заданных величин и вопроса задачи. | n – число всех вопросов m – число «хороших» вопросов, событие А – вопрос знакомый, n =30, m = 20. Найти р (А). |
| 2. | Найти формулу вероятности для данного случая
а) классическое определение 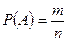 б) геометрическое определение
б) геометрическое определение  . .
| Задано общее число равновозможных событий n и число благоприятных событий m, следовательно, нужна формула а) классического определения вероятности:
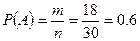 . .
|
Задача № 2-б. На квадратном участке дачи находится квадратный огород, сторона которого вдвое меньше стороны дачного участка. Найти вероятность того, что капля дождя, так долго ожидаемого на этой даче, попадет в огород.
Решение
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Ввести обозначения для заданных величин | а – длина стороны дачи,
а/2 – длина стороны огорода,
 - площадь дачи, где Ω – пространство элементарных исходов, - площадь дачи, где Ω – пространство элементарных исходов,
 - площадь огорода, где событие А – попадание капли дождя в огород – благоприятные исходы, тогда - площадь огорода, где событие А – попадание капли дождя в огород – благоприятные исходы, тогда
 , ,  . Найти Р(А). . Найти Р(А).
|
| 2. | Изобразить с помощью геометрических фигур полное пространство элементарных событий W и фигуру, соответствующую благоприятным исходам. | Нарисовать фигуру (отрезок, круг, полоса, куб и др.), соответствующую полному пространству событий W. Нарисовать внутри нее фигуру, соответствующую исходам, благоприятным для события А. В данном случае квадрат А расположен внутри квадрата W.. |
| 3. | Найти формулу вероятности для данного случая
а) классическое определение 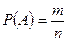 б) геометрическое определение
б) геометрическое определение  . .
| Т.к. события описываются с помощью геометрических фигур, то нужна формула б). Надо вычислить площади фигур А и W, сосчитать вероятность как отношение этих площадей по формуле P(A) 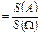 . Тогда . Тогда
 . .
|
Алгоритм на умение № 3
Вычисление вероятностей событий по известным вероятностям
других событий, с ними связанных
Задача № 3. Стрелок производит 3 выстрела по мишени. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,4; 0,5 и 0,7. Найти вероятность того, что в результате этих выстрелов окажется: а) одно попадание в мишень; б) хотя бы одно попадание; в) не более одного попадания.
Решение.
| № | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| Ввести обозначение для заданных величин | А 1 – попал при 1-м выстреле, А 2 – попал при 2-м выстреле, А 3 – попал при 3-м выстреле, В – одно попадание в мишень, С – хоты бы одно попадание в мишень, D – не более одного попадания. Р (А 1) = 0,4, Р (А 2) = 0,5, Р (А 3) = 0,7.Найти а) р (В), б) р (С), в) р (D). | |
| Найти формулу для этого случая | Надо найти вероятность событий по вероятностям событий, связанных с первыми – (п.1.2). Пользуемся формулами из п.1.2, выписав формулы связи между событиями, т.к. события А1, А2, А3 независимые, но совместные, имеем:
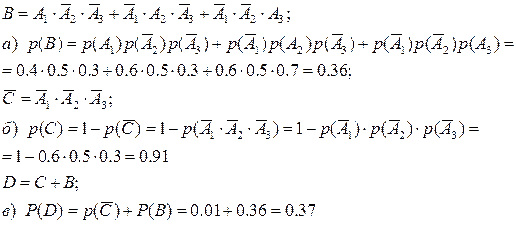
|
Алгоритм на умение № 4
Дата добавления: 2015-07-25; просмотров: 108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| III. Комплексные умения и алгоритмы к | | | Вычисление вероятностей событий с помощью соединений |