
Читайте также:
|
В первые классы школы должны быть приняты 200 детей. Вероятность появления среди принятых детей мальчика равна 0,515. Найти вероятность того, что среди них девочек и мальчиков будет поровну, и вероятность того, что мальчиков меньше, чем девочек.
Решение.
| № | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| Ввести обозначение для заданных величин | n – число детей m – число мальчиков р – вероятность того, что ученик мальчик (р = 0.515) q = 0.485 n = 200 Найти р 200(100) и р 200(m < n-m) = р 200 (m < n/ 2) = p 200 (m < 100) | |
| 10.Вычислить требуемую вероятность, используя, используя а)формулу Муавра-Лапласа, когда надо найти конкретное значение вероятности для m; б)интегральную формулу Лапласа, когда надо найти вероятность попадания в интервал [ m1,m2 ]. | а) Так как n велико, а р не мало и np > 10, нужно воспользоваться локальной теоремой Муавра-Лапласа, по которой рn(m) можно вычислить по формуле:
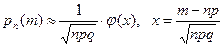 (значения j(х) содержится в таблице 3), np =103, (значения j(х) содержится в таблице 3), np =103, 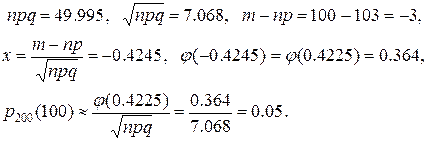 б) Для вычисления значения P 200 (m < 100) используют интегральную теорему Лапласа:
Рn(m 1£ m£m 2)= Ф(х 2 )-Ф(х 1 ), где
б) Для вычисления значения P 200 (m < 100) используют интегральную теорему Лапласа:
Рn(m 1£ m£m 2)= Ф(х 2 )-Ф(х 1 ), где
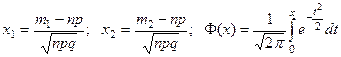 и
Ф(х) - функция Лапласа затабулирована (таблица 3), причем Ф(-х)=-Ф(х). и
Ф(х) - функция Лапласа затабулирована (таблица 3), причем Ф(-х)=-Ф(х).
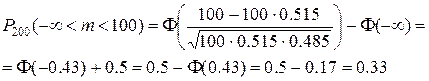 Воспользовались тем, что Ф(-х) = -Ф(х) и тем, что Ф(¥) = 0.5; значение Ф (0.43) взяли из таблицы 3.
Воспользовались тем, что Ф(-х) = -Ф(х) и тем, что Ф(¥) = 0.5; значение Ф (0.43) взяли из таблицы 3.
|
Комплексные умения и алгоритмы
к разделу 2 «Дискретные и непрерывные случайные величины»
| № | Умения | Алгоритмы |
| Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли. | 1. Ввести обозначения для заданных величин: числа испытаний, числа успехов, вероятности наступления события A, и выписать их значения. Выписать формулу Бернулли для искомой вероятности (по алгоритму 6).
2.Сосчитать требуемую вероятность, выбрав соответствующую содержанию задачи формулу Бернулли.
3. Найти числовые характеристики ДСВ по формулам МX = np, DX = npq и 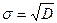 .
4.Составить ряд распределений случайной величины X – числа возможных образцов.
5.Составить функцию распределения случайной величины X – числа возможных образцов.
6. Построить график функции распределения ДСВ, учитывая значение накопительной вероятности на каждом интервале. .
4.Составить ряд распределений случайной величины X – числа возможных образцов.
5.Составить функцию распределения случайной величины X – числа возможных образцов.
6. Построить график функции распределения ДСВ, учитывая значение накопительной вероятности на каждом интервале.
| |
| Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании (геометрические распределения). | 1. Ввести обозначения для заданных величин: числа испытаний, числа успехов, вероятности наступления события A, и выписать их значения. Выписать формулу числа успехов геометрических распределений для искомой вероятности т.е. вероятности того, что событие впервые произойдет в k –ом испытании.
2.Сосчитать требуемую вероятность, выбрав соответствующую содержанию задачи формулу числа успехов успехов в k-ом испытании т.е. геометрических распределений  .
3.Найти числовые характеристики ДСВ по формулам МX = .
3.Найти числовые характеристики ДСВ по формулам МX = 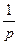 , DX = , DX =  и и 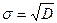 .
4. Составить ряд распределений случайной величины X – числа возможных образцов.
5.Составить функцию распределения случайной величины X – числа возможных образцов.
6.. Построить график функции распределения ДСВ, учитывая значение накопительной вероятности на каждом интервале. .
4. Составить ряд распределений случайной величины X – числа возможных образцов.
5.Составить функцию распределения случайной величины X – числа возможных образцов.
6.. Построить график функции распределения ДСВ, учитывая значение накопительной вероятности на каждом интервале.
| |
| Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов гипергеометрических распределений. | 1. Ввести обозначения для заданных величин: числа испытаний, числа успехов, вероятности наступления события A, и выписать их значения. Выписать формулу для искомой вероятности: если необходимо установить вероятность появления отдельных долей подмножеств, то используют гипергеометрические распределения.
2.Сосчитать требуемую вероятность, выбрав соответствующую содержанию задачи формулу числа успехов для гипергеометрических распределений (алгоритм 4-в).
3. Найти числовые характеристики ДСВ по общим формулам  , , 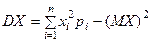 и и 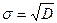 .
4.Составить ряд распределений случайной величины X – числа возможных образцов.
5.Составить функцию распределения случайной величины X – числа возможных образцов.
6. Построить график функции распределения ДСВ, учитывая значение накопительной вероятности на каждом интервале. .
4.Составить ряд распределений случайной величины X – числа возможных образцов.
5.Составить функцию распределения случайной величины X – числа возможных образцов.
6. Построить график функции распределения ДСВ, учитывая значение накопительной вероятности на каждом интервале.
| |
| Вычисление числовых характеристик ДСВ Z=f(X,Y). Вычисление вероятности попадания в интервал случайной величины Z=f(X,Y). | 1. Составить ряд распределений для одинаково распределенных случайных величин X, Y, Z=f(X,Y).
2. Вычислить математическое ожиданиепо формуле
MZ =  3. Вычислить дисперсиюпо формуле DZ=
3. Вычислить дисперсиюпо формуле DZ= 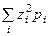 -MZ2 и среднеквадратичное отклонение s Z= -MZ2 и среднеквадратичное отклонение s Z= 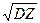 .
4. Вычислить вероятности попадания в интервал случайной величины Z=f(X,Y). .
4. Вычислить вероятности попадания в интервал случайной величины Z=f(X,Y).
| |
| Вычисление числовых характеристик НСВ, а также вероятность попадания НСВ Х в интервал P (a< Х < b) | 1.Записать функцию плотностивероятности f (x)=F|(x). 2.Вычислить математическое ожидание MX на указанном отрезке по формуле:  .
3.Вычислить дисперсию DХ на указанном отрезке по формуле .
3.Вычислить дисперсию DХ на указанном отрезке по формуле  и среднеквадратичное отклонение по формуле и среднеквадратичное отклонение по формуле 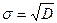 .
4.Найти моду, исследовав на экстремум функцию f(x) с помощью производной f |(x).
5.Найти медиану, решив уравнение .
4.Найти моду, исследовав на экстремум функцию f(x) с помощью производной f |(x).
5.Найти медиану, решив уравнение  .
6. Вычислить вероятность попадания в интервал (a;b) по формуле: P(a< Х < b)=Ф(b)-Ф(а).
7.Построить график функции плотностивероятности f (X) и функции распределения F(X). .
6. Вычислить вероятность попадания в интервал (a;b) по формуле: P(a< Х < b)=Ф(b)-Ф(а).
7.Построить график функции плотностивероятности f (X) и функции распределения F(X).
| |
| Вычисление числовых характеристик НСВ, равномерно распределенной на отрезке [a,b], а также вероятность попадания НСВ Х в интервал P (a< Х < b). | 1.Записать функция плотности вероятности f (x), определив границы интервала a и b.
2.Вычислить математическое ожидание MX по формуле для равномерных распределений MX =  3.Вычислить дисперсию DX по формуле для равномерных распределений
3.Вычислить дисперсию DX по формуле для равномерных распределений  .
4. Записать функцию распределения вероятности F(X), имеющую вид F(X)= .
4. Записать функцию распределения вероятности F(X), имеющую вид F(X)= 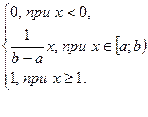 .
5.Вычислить вероятности попадания НСВ в интервал
P (a< Х < b) по алгоритму 13 (п.6). .
5.Вычислить вероятности попадания НСВ в интервал
P (a< Х < b) по алгоритму 13 (п.6).
| |
| Вычисление числовых характеристик НСВ, имеющей показательное распределение на отрезке [a,b] | 1. Записать функцию плотности вероятности f (x) показательного распределения для заданного значения l по формуле
f (x) =  2.Записать функцию распределения F (x) для заданного значения l по формуле
F (x) =
2.Записать функцию распределения F (x) для заданного значения l по формуле
F (x) = 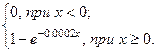 .
3.Вычислить математическое ожидание по формуле MX= .
3.Вычислить математическое ожидание по формуле MX= 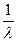 4.Вычислить дисперсию и среднеквадратичное отклонение по формулам DX=
4.Вычислить дисперсию и среднеквадратичное отклонение по формулам DX= 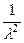 и и 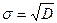 = = 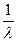 .
5. Вычислить вероятность попадания в интервал по формуле P(a<X<b)= .
5. Вычислить вероятность попадания в интервал по формуле P(a<X<b)=  . .
| |
| Определение числовых характеристик и вероятности попадания нормально распределенной НСВ Х в интервал P (a< Х < b). | 1.Записать математическое ожидание m и среднеквадратичное отклонение σ для нормально распределенной НСВ по закону N (m,σ).
2.Записать функцию плотности вероятности f (x) для нормально распределенной НСВ Х
3. Записать функцию распределения вероятности для нормально распределенной НСВ Х
4. Вычислить P (a < x < b), используя таблицы 3, по формуле
P(a <X< b)=Ф(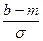 )-Ф( )-Ф( ).
5. Вычислить P (- d< x -m < d) или Р(|x-m|<d) по формуле
P(| x - a |<d)=2Ф( ).
5. Вычислить P (- d< x -m < d) или Р(|x-m|<d) по формуле
P(| x - a |<d)=2Ф( ), используя таблицы 3 (Приложение 1). ), используя таблицы 3 (Приложение 1).
| |
| Оценить с помощью неравенства Чебышева вероятность того, что НСВ Х отличается от среднего на величину e | 1.Записать условие символически: математическое ожидание mX, среднеквадратичное отклонение s, дисперсия DX.
2. Подставить значения mX, DX и eв неравенство Чебышева
P (| X - mX | ≥ e) ≤ 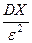 , если надо оценить вероятность того, что НСВ отличается от среднего на величину, больше, чем e.
3. Подставить значения mX, DX и eв неравенство Чебышева
P (| X - mX | < e) ≥1- , если надо оценить вероятность того, что НСВ отличается от среднего на величину, больше, чем e.
3. Подставить значения mX, DX и eв неравенство Чебышева
P (| X - mX | < e) ≥1- 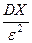 , если надо оценить вероятность того, что НСВ отличается от среднего на величину, меньше, чем e. , если надо оценить вероятность того, что НСВ отличается от среднего на величину, меньше, чем e.
|
Алгоритм 9
Дата добавления: 2015-07-25; просмотров: 255 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона | | | Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли. |