Подставив значения тригонометрических функций в модель Фурье, получить прогнозное значение уровня ряда динамики.
При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные | Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной | Способ 1. Этот способ основан на проверке гипотезы о значимости коэффициента линейной корреляции с помощью t – критерия Стьюдента. | Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера. | Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации (см. задачу 9, п. 7). | С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно | Для заметок | Временная разность между данным и следующим уровнем. | В частности, если тренд – линейный, то | При этом - значение уровня ряда динамики в момент времени в данный момент времени (сезон) , а - среднее значение уровней ряда динамики. |
Осуществляем прогноз. Январь, февраль и март 2009 года являются
Соответственно 13, 14 и 15 периодом от начала отсчета (январь 2008 года). Согласно результатам задач 13 и 14 получаем следующие прогнозы:
Январь: 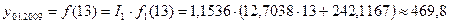 (тыс. руб.);
(тыс. руб.);
Февраль: 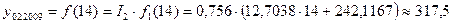 (тыс. руб.);
(тыс. руб.);
Март:  (тыс. руб.).
(тыс. руб.).
Прогнозируем объем реализации по модели Фурье:
Январь:  ;
;  или
или
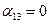 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
; 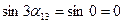 ;
;
m = 1: 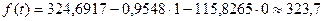 (тыс. руб.);
(тыс. руб.);
m = 2: 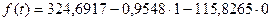
 (тыс. руб.);
(тыс. руб.);
m = 3: 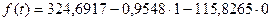

 (тыс. руб.);
(тыс. руб.);
Февраль:  ;
;  или
или
 ;
; 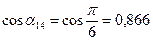 ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
m = 1:  (тыс. руб.);
(тыс. руб.);
m = 2: 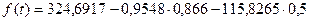 -
-
 (тыс. руб.);
(тыс. руб.);
m = 3: 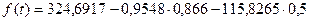
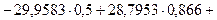
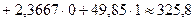 (тыс. руб.);
(тыс. руб.);
Март:  ;
;  или
или
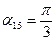 ;
; 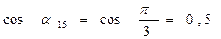 ;
; 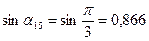 ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
m = 1:  (тыс. руб.);
(тыс. руб.);
m = 2:  -
-
 (тыс. руб.);
(тыс. руб.);
m = 3: 
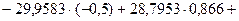
 (тыс. руб.).
(тыс. руб.).

Дата добавления: 2015-07-25; просмотров: 44 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.007 сек.)

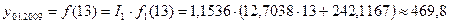 (тыс. руб.);
(тыс. руб.);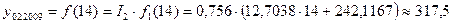 (тыс. руб.);
(тыс. руб.); (тыс. руб.).
(тыс. руб.). ;
;  или
или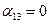 ;
;  ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
; 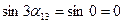 ;
;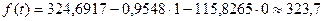 (тыс. руб.);
(тыс. руб.);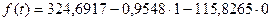
 (тыс. руб.);
(тыс. руб.);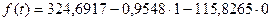

 (тыс. руб.);
(тыс. руб.); ;
;  или
или ;
; 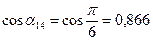 ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;  ;
; (тыс. руб.);
(тыс. руб.);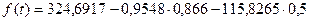 -
- (тыс. руб.);
(тыс. руб.);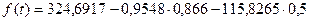
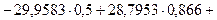
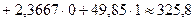 (тыс. руб.);
(тыс. руб.); ;
;  или
или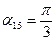 ;
; 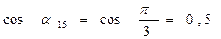 ;
; 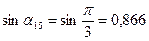 ;
; ;
;  ;
;  ;
; ;
;  ;
;  ;
; (тыс. руб.);
(тыс. руб.); -
- (тыс. руб.);
(тыс. руб.);
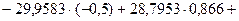
 (тыс. руб.).
(тыс. руб.).