
Читайте также:
|
Среднее значение абсолютного прироста равно:
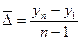 .
.
Величина среднего значения коэффициента роста равна:
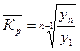 .
.
Среднее значение темпов роста подсчитывается по формуле:
 .
.
Наконец, среднее значение темпов прироста рассчитывается следующим образом:
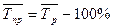 .
.
Переходим к решению задачи. Так как значения уровней приведены на определенную дату (конец месяца), временная разность между уровнями постоянная (1 месяц), то рассматриваемый ряд динамики является моментным с равноотстоящими уровнями.
Найдем числовые характеристики уровня ряда динамики. Результаты расчетов помещены в таблицу 13.
В качестве примера произведем анализ строки таблицы 13, соответствующей октябрю месяцу. В октябре 2008 года магазин реализовал продукции на 523,2 тыс. руб., что на 27,8 тыс. руб. больше по сравнению с сентябрем и на 148,6 тыс. руб. больше по сравнению с январем 2008 года. Следовательно, реализация продукции в октябре увеличилась в 1,0561 раза по сравнению с октябрем и в 1,3967 раза по сравнению с январем. Уровень реализации в октябре составил 105,6116% от сентябрьского и 139,669% от январского уровня реализации. Таким образом, продукции в октябре реализовано на 5,6116% больше по сравнению с сентябрем и на 39,669% больше по сравнению с январем месяцем. Величина абсолютной величины одного процента прироста составила 4,954 тыс. руб.
Таблица 13
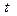
| 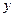
|  , тыс. руб. , тыс. руб.
| 
|  , % , %
| 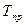 , % , %
| |%|, тыс. руб. | ||||
| С пред. месяцем | С январем 2008 г. | С пред. месяцем | С январем 2008 г. | С пред. месяцем | С январем 2008 г. | С пред. месяцем | С январем 2008 г. | |||
| 374,6 | - | - | - | - | - | |||||
| 245,5 | -129,1 | -129,1 | 0,6554 | 0,6554 | 65,5366 | 65,5366 | -34,4634 | -34,4634 | 3,746 | |
| 304,6 | 59,1 | -70 | 1,2407 | 0,8131 | 124,0733 | 81,3134 | 24,0733 | -18,6866 | 2,455 | |
| 171,1 | -133,5 | -203,5 | 0,5617 | 0,4568 | 56,1720 | 45,6754 | -43,8280 | -54,3246 | 3,046 | |
| 210,8 | 39,7 | -163,8 | 1,2320 | 0,5627 | 123,2028 | 56,2734 | 23,2028 | -43,7266 | 1,711 | |
| 321,3 | 110,5 | -53,3 | 1,5242 | 0,8577 | 152,4194 | 85,7715 | 52,4194 | -14,2285 | 2,108 | |
| 244,7 | -76,6 | -129,9 | 0,7616 | 0,6532 | 76,1594 | 65,3230 | -23,8406 | -34,6770 | 3,213 | |
| 345,6 | 100,9 | -29 | 1,4123 | 0,9226 | 141,2342 | 92,2584 | 41,2342 | -7,7416 | 2,447 | |
| 495,4 | 149,8 | 120,8 | 1,4334 | 1,3225 | 143,3449 | 132,2477 | 43,3449 | 32,2477 | 3,456 | |
| 523,2 | 27,8 | 148,6 | 1,0561 | 1,3967 | 105,6116 | 139,6690 | 5,6116 | 39,6690 | 4,954 | |
| 385,3 | -137,9 | 10,7 | 0,7364 | 1,0286 | 73,6430 | 102,8564 | -26,3570 | 2,8564 | 5,232 | |
| 274,2 | -111,1 | -100,4 | 0,7117 | 0,7320 | 71,1653 | 73,1981 | -28,8347 | -26,8019 | 3,853 |
Найдем среднее значение уровней ряда динамики. Имеем: среднемесячный объем реализации продукции магазином составил в 2008 году

324,7 (тыс. руб.).
Так как
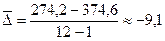 ,
,
то заключаем, что ежемесячное падение объемов реализации продукции в 2008 году составляло в среднем 9,1 тыс. руб.
Среднее значение коэффициента роста равно
 .
.
Это означает, что месячный уровень объема реализации составляет в среднем 0,972 от предыдущего месяца или (согласно формуле среднего значения темпов роста)
 .
.
Итак, в среднем в месяц, объем продаж сокращался на 2,8% по сравнению с предыдущим месяцем, так как
 .
.
Задача 12. По данным задачи 11 (рассмотреть данные 2008 года) построить уравнение линейной функции тренда.
На формирование значение уровней ряда динамики основное влияние оказывают долговременные факторы, формирующие общую, в длительной перспективе тенденцию развития признака. Результат действия этих факторов моделируется в виде функции тренда
 .
.
Дата добавления: 2015-07-25; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Для заметок | | | В частности, если тренд – линейный, то |