В зависимости от r имеем следующую интерпретацию связи

Где и - ординаты точек кумулятивной кривой, абсциссы которых раны β и α соответственно. | Где и - частоты интервала, предшествующего и следующего за модальным соответственно. | Верхний параметр, р равно 0,25 (квартиль), 0,1 (дециль), 0,01 (перцентиль). | Среднее значение (средняя арифметическая) | Находим шаг варьирования , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности - постоянная величина. | Причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности | Где - выборочная доля (m– количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная | Для заметок | Г) если |as|<1, |es|<1 – распределение нормального типа. | Чтобы убедиться, что теоретические частоты адекватно описывают эмпирические данные, на одном чертеже строим кривую нормального распределения и полигон частот. |

Читайте также:

Значение r	Интерпретация связи
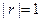
	Линейная функциональная
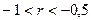
	Линейная обратная
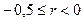
	Нелинейная
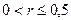
	Нелинейная
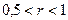
	Линейная прямая
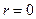
	Отсутствует

Степень тесноты корреляционной связи устанавливается с помощью корреляционного отношения η, равного

,

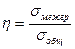Дата добавления: 2015-07-25; просмотров: 50 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами	\|	При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные

mybiblioteka.su - 2015-2024 год. (0.006 сек.)
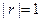
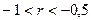
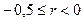
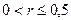
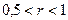
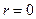
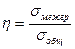