Для заметок

Задача 2. | Задача 4. | А) середину интервала | Г) относительную частоту | Где и - ординаты точек кумулятивной кривой, абсциссы которых раны β и α соответственно. | Где и - частоты интервала, предшествующего и следующего за модальным соответственно. | Верхний параметр, р равно 0,25 (квартиль), 0,1 (дециль), 0,01 (перцентиль). | Среднее значение (средняя арифметическая) | Находим шаг варьирования , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности - постоянная величина. | Причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности |

Читайте также:

Тема 2. «Проверка статистических гипотез»

Задача 8. С вероятностью 0,95 проверить гипотезу о том, что генеральная совокупность, которой принадлежит выборка из задачи 1, распределена по нормальному (Гауссову) закону распределения случайной величины.

Гипотеза о нормальном распределении генеральной совокупности, которой принадлежит исследуемая выборка, с доверительной вероятностью γ проверяется с помощью 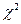- критерия согласия Пирсона (критерия хи - квадрат). Приведем алгоритм проверки гипотезы с помощью этого критерия.

Дата добавления: 2015-07-25; просмотров: 50 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Где - выборочная доля (m– количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная	\|	Г) если \|as\|<1, \|es\|<1 – распределение нормального типа.

mybiblioteka.su - 2015-2024 год. (0.006 сек.)