Читайте также:
|
t = 3, если γ =0,99,
t = 2, если γ =0,95,
t = 1, если γ =0,63,
μ – средняя ошибка выборки, равная
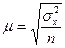- если отбор случайный – повторный,
- если отбор случайный – бесповторный.
Имеем (см. задачу 4):
, 
, n = 100, N = 1500, t = 2.
Средняя ошибка выборки равна:
,
,
Если отбор повторный или бесповторный соответственно. Тогда, в зависимости от типа отбора, предельная ошибка выборки равна:
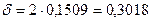или 
.
Получаем: нижняя граница доверительного интервала:
;
верхняя граница доверительного интервала:
.
Итак, с вероятностью 0,95 можно утверждать, что средний диаметр детали, изготавливаемой предприятием находится в пределах от 21,1582 до 21,7618 мм (если выборка организована методом случайного повторного отбора) и от 21,1684 до 21,7516 мм (если выборка случайная, бесповторная).
Задача 7. Для выборки из задачи 1 с вероятностью γ = 0,99 определить границы интервала, в котором заключена генеральная доля признака р – диаметр детали, находящийся в пределах от 20 до 23 мм включительно и сделать соответствующие выводы. Задачу решить в предположении бесповторного отбора из генеральной совокупности объема N = 2000.
С доверительной вероятностью γ утверждается, что математическое ожидание р принадлежит интервалу:
,
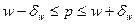Дата добавления: 2015-07-25; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Находим шаг варьирования , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности - постоянная величина. | | | Где - выборочная доля (m– количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная |