
Читайте также:
|
Величина ложного нуля определяется как значение случайной величины, имеющее максимальную частоту.
3. Для каждого значения х определяем условные варианты
.
4. Вычисляем условные моменты:
;;;.
5. Искомые значения рассчитываются по формулам:
 ;
;
 ;
;
 ;
;
.
Из группированного статистического ряда (см задачу 1) заключаем, что
 = 1.
= 1.
Так как максимальной частоте ряда 28 соответствует значение случайной величины 21,5 (см. группированный статистический ряд, задача 1), то
 =21,5.
=21,5.
Отсюда, условный вариант
.
Нахождение условных моментов удобно производить в таблице:
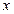
| 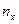
| 
| 
| 
| 
| 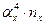
|
| 18,5 | -3 | -9 | -81 | |||
| 19,5 | -2 | -22 | -88 | |||
| 20,5 | -1 | -27 | -27 | |||
| 21,5 | ||||||
| 22,5 | ||||||
| 23,5 | ||||||
| 24,5 | ||||||
| 25,5 | ||||||
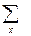
| - | -4 |
Тогда, условные варианты соответственно равны:
;;;.
Итак, требуемые величины соответственно равны:
 ;
;
 ;
; 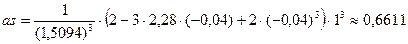 ;
;
.
Задача 6. Для выборки из задачи 1 с вероятностью γ = 0,95 определить границы интервала, в котором заключено математическое ожидание а (генеральная средняя или среднее значение генеральной совокупности) и сделать соответствующие выводы. Задачу решить в предположении а) повторного, б) бесповторного отбора из генеральной совокупности объема
N = 1500.
С доверительной вероятностью γ утверждается, что математическое ожидание а принадлежит интервалу:
 ,
,
Дата добавления: 2015-07-25; просмотров: 90 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Среднее значение (средняя арифметическая) | | | Причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности |