
Читайте также:
|





Рис. 6
Составляем расчетную таблицу. В ней выделяем первые отрицательные разности и по ним смотрим интервалы, содержащие искомые параметры. Также выделяем максимальную частоту, которой соответствует модальный интервал. Напомним, что в рассматриваемой задаче объем выборки равен 100, а длина каждого интервала группировки равна 1.
| (α;β) | х | 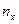
| 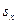
| 50- 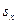
| 
| 
| 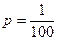
| |||
25- 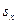
| 75- 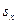
| 10- 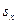
| 90- 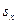
| 1- 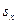
| 99- 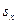
| |||||
| (18;19) | 18,5 | -2 | ||||||||
| (19;20) | 19,5 | -4 | -13 | |||||||
| (20;21) | 20,5 | -16 | -31 | -40 | ||||||
| (21;22) | 21,5 | -19 | -44 | -59 | -68 | |||||
| (22;23) | 22,5 | -38 | -63 | -13 | -78 | -87 | ||||
| (23;24) | 23,5 | -43 | -68 | -18 | -83 | -3 | -92 | |||
| (24;25) | 24, | -46 | -71 | -21 | -86 | -6 | -95 | |||
| (25;26) | 25,5 | -50 | -75 | -25 | -90 | -10 | -99 | -1 |
Получаем:
 (мм);
(мм);
 (мм);
(мм);
 (мм),
(мм), 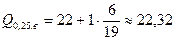 (мм);
(мм);
 (мм),
(мм),  (мм);
(мм);
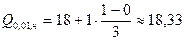 (мм),
(мм), 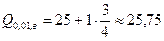 (мм).
(мм).
Делаем выводы.
1. Наиболее часто встречающийся диаметр детали в выборочной совокупности составляет 21,1 мм.
2. В интервале (18;21,32) находится 50% деталей с минимальной величиной диаметра, а в интервале (23,32;26) – 50% деталей с максимальной величиной диаметра.
3. В интервалах (18;20,41), (18;19,64), (18;18,33) находятся соответственно 25%, 10% и 1% деталей с минимальным значением признака, а такая же доля деталей с максимальным значением признака принадлежит интервалам (22,32;26), (23,4;26), (25,75;26).
Задача 4. Для выборки из задачи 1 найти среднее значение и показатели вариации (среднее линейное отклонение, дисперсию, расчет которой произвести двумя способами, то есть по определению и по формуле разностей, среднее квадратическое отклонение, коэффициент вариации, асимметрию и эксцесс).
Согласно соответствующим определениям, имеем:
Дата добавления: 2015-07-25; просмотров: 94 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Где и - частоты интервала, предшествующего и следующего за модальным соответственно. | | | Среднее значение (средняя арифметическая) |