Г) если |as|<1, |es|<1 – распределение нормального типа.
Задача 4. | А) середину интервала | Г) относительную частоту | Где и - ординаты точек кумулятивной кривой, абсциссы которых раны β и α соответственно. | Где и - частоты интервала, предшествующего и следующего за модальным соответственно. | Верхний параметр, р равно 0,25 (квартиль), 0,1 (дециль), 0,01 (перцентиль). | Среднее значение (средняя арифметическая) | Находим шаг варьирования , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности - постоянная величина. | Причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности | Где - выборочная доля (m– количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная |
5. Производим частот теоретических частот  каждого из интервалов группировки (α;β), рассчитанных в предположении, что выборочная совокупность распределена по нормальному закону распределения:
каждого из интервалов группировки (α;β), рассчитанных в предположении, что выборочная совокупность распределена по нормальному закону распределения:
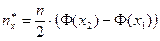 ,
,
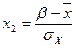 ,
, 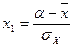 ,
,
Где - функция Лапласа, значения которой приведены в таблице 1 Приложения. Заметим, что функция Лапласа – нечетная, то есть.
Дата добавления: 2015-07-25; просмотров: 63 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.008 сек.)

 каждого из интервалов группировки (α;β), рассчитанных в предположении, что выборочная совокупность распределена по нормальному закону распределения:
каждого из интервалов группировки (α;β), рассчитанных в предположении, что выборочная совокупность распределена по нормальному закону распределения: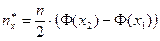 ,
,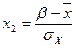 ,
, 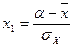 ,
,