Барометрическая формула. Распределение Больцмана

Лекция 12.

Термодинамические функции состояния. Функции распределения. Классическая и квантовая статистики. Статистические распределения. (2 часа)

12.1. Микроскопические параметры. Вероятность и флюктуации. Распределение молекул /частиц/ по абсолютным значениям скорости. Распределение Максвелла.

12.2. Средняя кинетическая энергия частицы. Скорости теплового движения частиц.

12.3. Распределение Больцмана.

12.4. Теплоемкость многоатомных газов. Ограниченность классической теории теплоемкостей.

12.5. Статистический смысл термодинамических потенциалов и температуры. Роль свободной энергии.

12.6. Распределение Гиббса для системы с переменным числом частиц.

12.7. Принцип Нернста и его следствия.

Демонстрации:

1. Распределение молекул по скоростям.

2. Атмосферное давление.

Распределение молекул по скоростям.

Распределение Максвелла

Основные понятия теории вероятностей

Впервые решил задачу распределения молекул по скоростям Максвелл в 1859 году.

Пусть мы имеем ансамбль из N молекул

Параметр Х - принимает значения Х1;X2;X3.........Xi........

которые выпали соответственно N1,N2,N3........Ni......раз..

Ni -- число молекул у которых параметр Х принимает значение Хi, тогда отношение

Pi= Ni/ N

вероятность того что параметр Х имеет значение Xi

Пример: ИГРАЛЬНАЯ КОСТЬ

Кость имеет 6 граней, она должна быть однородной. Будем бросать кость 6 000 раз. События Хi -выпадание той или иной цифры от 1 до 6

Пусть 1выпадает 999 раз P₁=999/6000=1/6

2- выпадает 1001 раз P₂=1001/6000= 1/6

3- выпадает 998 раз P₃=998/6000 = 1/6

4- выпадает 1003 раз P₄=1003/6000= 1/6

5- выпадает 996 раз P5=996/'6000 = 1/6

6- выпадает 1000 раз P6=1000/6000 =1/6

----------------------------------

Сумма общего числа испытаний равняется 6 000, а вероятность каждого из событий равна 1/6

Если же за N возьмем не 6 000 а 60 000, то вероятность Pi каждого из событий еще ближе к 1/6.

СВЯЗЬ СРЕДНЕГО ЗНАЧЕНИЯ С ВЕРОЯТНОСТЬЮ

Если же случайные события или параметр Х изменяется не дискретно, а непрерывно, то

dP(x)=F(X)dx

представляет собой вероятность нахождения параметра Х в интервале от Х до Х+dX

F(X)-- плотность вероятности или функция распределения вероятности.

Тогда число молекул, у которых значение параметра Х принадлежит интервалу от X до dX определяется, соотношением:

dN=NdP(x)=NF(х)dх

РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА

Скорость молекулы тоже случайная величина, тогда число молекул (dNv) модуль скорости которых лежит в интервале от V до V+dV определяется соотношением:

dN(v)=NdP: dP(v)=F(V)dV: dN=NF(V)dV

где F(V) -- функция распределения вероятности значения скорости

Основное уравнение молекулярно-кинетической теории приводит к выводу о том, что средний квадрат скорости молекул зависит от температуры газа и определяется формулой

,

которую можно также представить в виде

.

Величину - называют среднеквадратичной скоростью. Будем обозначать ее

.

Расчеты показывают, что величина среднеквадратичной скорости молекул азота (воздуха) при нормальных условиях равна

Очевидно, что при хаотическом движении молекулы газа имеют не одинаковые скорости. Их величина с течением времени непрерывно изменяется. Скорости молекул могут принимать любые значения в интервале от 0 и до бесконечности. Однако средние характеристики этого движения имеют вполне определенные численные значения, зависящие только от температуры газа. Впервые закон распределения скоростей молекул был получен Дж. Максвеллом в 1859 году. В соответствии с этим законом доля молекул, скорости которых принадлежат заданному интервалу скоростей от до , определяется соотношением

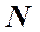Здесь - число всех молекул в сосуде,

- число молекул, скорости которых принадлежат заданному интервалу скорости (от 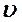до ),

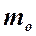- масса молекулы,

- абсолютная температура,

- постоянная Больцмана.

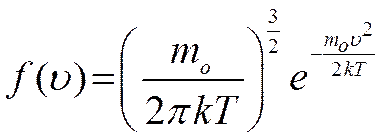- плотность вероятности

Приведенное соотношение называют законом распределением Максвелла по скоростям молекул. Как оказалось распределение Максвелла справедливо не только для газов. По закону Максвелла распределены скорости молекул жидкостей и твердых тел. Распределение Максвелла удобно проанализировать с помощью диаграммы, на которой представлена зависимость функции распределения 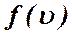от скорости . Функция распределения Максвелла имеет вид:

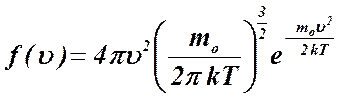
На приведенной диаграмме площадь узкой полоски численно равна доле молекул, скорости которых принадлежат заданному интервалу скоростей, а площадь под кривой численно равна единице, т.к. характеризует молекулы, скорости которых принимают любые значения от 0 до .

Скорость, соответствующую максимуму функции распределения называют наиболее вероятной скоростью. Величину наиболее вероятной скорости можно определить из условия экстремума функции распределения. Дифференцируя функцию распределения и приравнивая полученный результат нулю, получим:

.

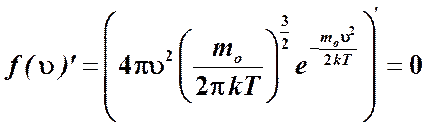
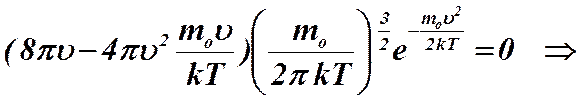
Как видим, наиболее вероятная скорость меньше среднеквадратичной скорости. С помощью распределения Максвелла можно рассчитать также среднюю скорость молекул газа. Ее величина определяется формулой

.

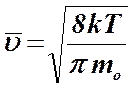Более удобными для расчетов среднеквадратичной, наиболее вероятной и средней скоростей молекул формулы приведены ниже:

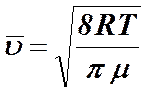
Отношение скорости молекулы к наиболее вероятной скорости ансамбля молекул называют приведенной или относительной скоростью молекулы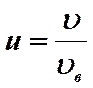

Распределение Максвелла для приведенной скорости:

Сколько молекул в моле имеют скорости, отличающиеся от наиболее вероятной, не более чем на 10% или 0.1

Распределение Максвелла получило экспериментальное

подтверждение в 1920 г. в опытах Штерна.

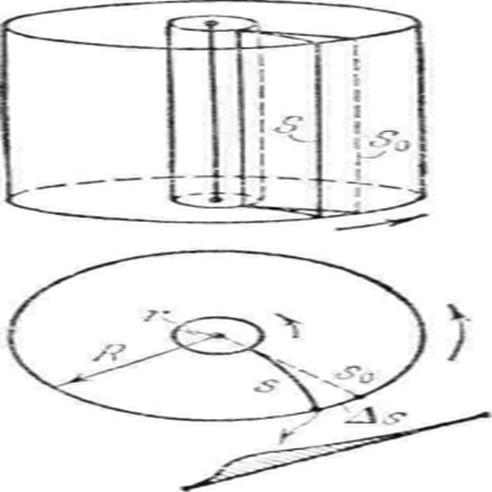
Опыты Штерна сводились к следующему. Два коаксиальных цилиндра приводились в быстрое вращение. На внутренней поверхности большого цилиндра осаждались пары серебра, которые в виде узкого пучка выходили из узкой щели малого цилиндра. Внутри большого цилиндра поддерживался глубокий вакуум. Вдоль оси малого цилиндра располагалась тонкая нить, покрытая тонким слоем серебра и нагреваемая электрическим током. В соответствии с представлениями молекулярно-кинетической теории скорости атомов серебра распределены по закону Максвелла. Величину скорости атомов серебра можно определить по формуле:

,

в которой - радиус большого цилиндра, - угловая скорость вращения цилиндров, - величина, характеризующая положение осажденного атома серебра.

Прямые измерения указанных величин и анализ плотности осажденных атомов серебра приводят к выводу о том, что Максвелловский закон распределения по скоростям полностью подтверждается данным экспериментом.

Барометрическая формула. Распределение Больцмана

Сравним атмосферное давление на двух близких горизонтальных уровнях. В соответствии с известными законами гидростатики давление на более низком уровне

превосходит давление на более высоком уровне на величину . В силу этого получим

.

В соответствии с уравнением Менделеева-Клапейрона плотность воздуха будет равна

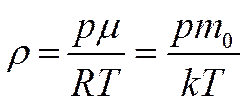. Учитывая это, далее получим

Выполняя интегрирование приведенного соотношения, получим

.

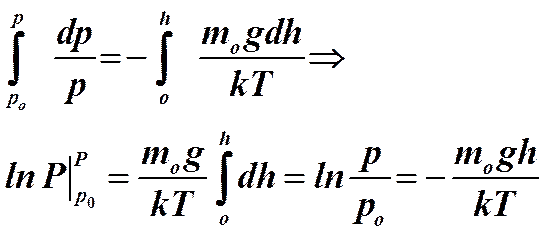После потенцирования получим известную барометрическую формулу Больцмана

Приведенная формула передает характер изменения давления с высотой в изотермической атмосфере. Из нее следует, что с увеличением высоты атмосферное давление уменьшается по экспоненциальному закону. Быстрота уменьшения давления существенно зависит от массы молекул газа. Быстрее убывает парциальное давление газов, молекулы которых имеют большую массу. Из барометрической формулы легко получить соотношения, связывающие плотности и концентрации молекул воздуха на разных высотах

, .

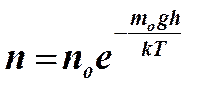Больцман обратил внимание на то, что в барометрической формуле величина представляет собой потенциальную энергию молекул газа, находящихся в гравитационном поле, и пришел к выводу о том, что открытое им распределение представляет собой универсальный закон распределения молекул по их потенциальным энергиям. Принимая во внимание распределение Максвелла по скоростям (кинетическим энергиям молекул) и распределение Больцмана по потенциальным энергиям, Гиббс пришел к выводу о том, что для частиц, движение и взаимодействие которых описываются законами Ньютона, справедлив универсальный закон распределения по их энергиям. Согласно этому закону число частиц, обладающих данной энергией, пропорционально экспоненциальному множителю

.

Другими словами, для частиц с энергиями 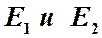выполняется соотношение

_.

Барометрическая формула Больцмана была использована Перреном в (1908 – 1913) для экспериментального определения числа Авогадро. Опыт Перрена сводился к изучению распределения малых частиц, взвешенных в жидкости. Перрен с помощью микроскопа подсчитывал число взвешенных в жидкости частиц (краски гуммигута) на различных высотах и, полагая, что они распределены по закону Больцмана

,

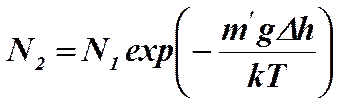рассчитал постоянную Больцмана по формуле

В приведенной формуле 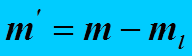- эффективная масса частицы, - расстояние между уровнями, для которых подсчитывалось количество частиц, наблюдаемых в поле зрения микроскопа, - абсолютная температура, - число частиц на выделенных горизонтальных уровнях.

.

Дата добавления: 2015-07-25