Чтобы убедиться, что теоретические частоты адекватно описывают эмпирические данные, на одном чертеже строим кривую нормального распределения и полигон частот.

7. Находим наблюдаемое значение критерия Пирсона по формуле:

.

С вероятностью γ выдвигаем гипотезу о нормальном распределении генеральной совокупности, которой принадлежит выборка. Для этого по таблице 2 Приложения критических значений критерия Пирсона определяем критическое значение

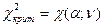, α = 1- γ, ν = k -3,

k – число интервалов группировки. Выводы производятся на основании следующего утверждения: если

,

То гипотеза о нормальном распределении генеральной совокупности, которой принадлежит исследуемая выборка, принимается с указанной вероятностью. В противном случае гипотеза отвергается с той же вероятностью.

Сравнивая рисунки 4 и 7, делаем вывод об их похожести.

Сравнивая рисунки 6 и 8, делаем вывод об их похожести.

Согласно задаче 4 (или 5)

, ,

следовательно (см. таблицу 9) рассматриваемое распределение является левосторонним островершинным.

Так как одновременно

, ,

то наше распределение имеет нормальный тип.

Используем результаты решения задач 4 и 5:

n = 100, , .

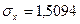Тогда, теоретические частоты рассчитываются так:

,

, .

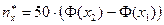Находим их в расчетной таблице:

(α;β)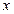
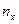
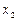
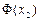
(18;19)	18,5		-1,63	-0,8969	-2,29	-0,9780	4,055
(19;20)	19,5		-0,97	-0,6679	-1,63	-0,8969	11,450
(20;21)	20,5		-0,30	-0,2358	-0,97	-0,6679	21,605
(21;22)	21,5		0,36	0,2812	-0,30	-0,2358	25,850
(22;23)	22,5		1,02	0,6923	0,36	0,2812	20,555
(23;24)	23,5		1,68	0,9070	1,02	0,6923	10,735
(24;25)	24,5		2,35	0,9812	1,68	0,9070	3,710
(25;26)	25,5		3,01	0,9974	2,35	0,9812	0,810

На одном графике (рисунок 9) строим кривую теоретических частот (сплошная линия) и полигон частот (пунктирная линия).

Рис. 9

Сравнение графиков наглядно показывает, что найденные результаты расчетов адекватно описывают эмпирические данные.

Находим наблюдаемое значение критерия Пирсона. Расчеты производим в таблице:

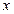
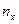
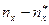
18,5		4,055	-1,055	1,113025	0,3710
19,5		11,450	-0,450	0,202500	0,0184
20,5		21,605	5,395	29,106025	1,0780
21,5		25,850	2,150	4,622500	0,1651
22,5		20,555	-1,555	2,418025	0,1273
23,5		10,735	-5,735	32,890225	6,5780
24,5		3,710	-0,710	0,504100	0,1680
25,5		0,810	3,190	10,176100	2,5440
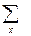
	-	-	-	-	11,0499

Итак,

.

Доверительная вероятность γ = 0,95, отсюда уровень значимости

α = 1-0,95 = 0,05. Число интервалов группировки k = 8, тогда ν = 8 -3 = 5. Отсюда, критическое значение согласно таблице 2 Приложения равно

.

Так как

11,0499<11,1,

то гипотеза о том, что генеральная совокупность, которой принадлежит выборка из задачи 1, распределена нормально, принимается с вероятностью 0,95.

Для заметок

Тема 3. «Корреляционно – регрессионный анализ»

Задача 9. Было произведено выборочное обследование 50 предприятий с целью выяснения взаимосвязи между среднегодовой стоимостью основных производственных фондов (млн. руб.) и затратами на капитальный ремонт (в % от стоимости основных производственных фондов). Результаты представлены в таблице:

Затраты на капитальный ремонт (в % к стоимости основных производственных фондов)	Среднегодовая стоимость основных производственных фондов, млн. руб.	Итого
(5;9)	(9;13)	(13;17)	(17;21)	(21;25)	(25;29)
(1;3)
(3;5)
(5;7)
(7;9)
(9;11)
(11;13)
(13;15)
Итого

Необходимо:

а) произвести все необходимые вычисления;

б) построить эмпирические линии регрессии и сделать первоначальные выводы о форме корреляционной связи;

в) определить величину коэффициента линейной корреляции (по определению и методом моментов) и сделать выводы о форме корреляционной зависимости;

г) найти значение корреляционного отношения и сделать выводы о тесноте корреляционной связи;

д) с вероятностью 0,95 проверить гипотезу о статистической значимости эмпирических данных;

е) установить вид уравнения регрессии y на x и x на y в предположении прямой (расчет коэффициентов произвести двумя способами), параболической и показательной регрессионной моделей;

ж) с помощью величины средней ошибки аппроксимации и индекса детерминации отобрать наиболее точную модель;

з) построить на одном чертеже эмпирические данные и линии регрессии;

и) произвести прогноз уровня затрат на капитальный ремонт, если стоимость основных производственных фондов равна 2,5 млн. руб., а также спрогнозировать величину основных производственных фондов, если затраты на капитальный ремонт составляют 0,52% от ОПФ.

1. Эмпирические данные принято записывать в виде корреляционной таблицы (если группировочный признак представлен в виде интервала, то необходимо найти его середину):

Х Y

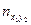
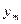
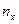
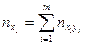
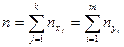
В ней: x – значение признака X, - его частота, y – значение признака Y, - его частота, n – объем выборки, а - частота пары (х;у) (если среди эмпирических данных пара отсутствует, то в соответствующей клетке корреляционной таблицы не ставим никакой цифры).

Дата добавления: 2015-07-25