
Читайте также:
|
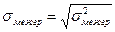 ,
, 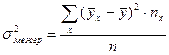 ,
,
 .
.
Характер связи определяется так:
| Значение η | Характер связи |
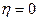
| Отсутствует |
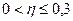
| Практически отсутствует |

| Слабая |

| Умеренная |

| Сильная |

| Функциональная |
Для проверки правильности произведенных вычислений удобно использовать свойство корреляционного отношения:
 .
.
Проверить гипотезу о статистической значимости эмпирических данных, а следовательно о принципиальной возможности построения уравнения регрессионной модели можно с помощью t - критерия Стьюдента.
Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,
 ,
,
То это с вероятностью γ (уровнем значимости α = 1- γ ) говорит о значимости коэффициента линейной корреляции, а следовательно о статистической значимости эмпирических данных. При этом
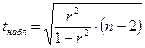 ,
,
а критическое значение определяется по таблице (см. таблицу 3 Приложения):
 , α = 1- γ, ν = n – 2.
, α = 1- γ, ν = n – 2.
Нахождение параметров уравнений линий регрессии у на х и х на у производится путем решения соответствующих систем нормальных уравнений. Для линейного случая существует еще один, упрощенный способ. Вид уравнений линейной, параболической и показательной регрессий и способы расчета их параметров помещены в таблицу 10.
Дата добавления: 2015-07-25; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В зависимости от r имеем следующую интерпретацию связи | | | Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной |