В частности, если тренд – линейный, то

Чтобы убедиться, что теоретические частоты адекватно описывают эмпирические данные, на одном чертеже строим кривую нормального распределения и полигон частот. | Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами | В зависимости от r имеем следующую интерпретацию связи | При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные | Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной | Способ 1. Этот способ основан на проверке гипотезы о значимости коэффициента линейной корреляции с помощью t – критерия Стьюдента. | Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера. | Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации (см. задачу 9, п. 7). | С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно | Для заметок |

Читайте также:

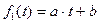Параметры a и b могут быть найдены методом наименьших квадратов путем решения системы нормальных уравнений:

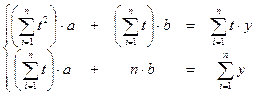Решая ее, получаем:

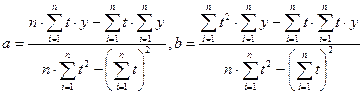Все необходимые расчеты делаем в таблице:


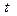
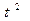
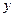
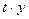
			374,6	374,6
			245,5
			304,6	913,8
			171,1	684,4
			210,8
			321,3	1927,8
			244,7	1712,9
			345,6	2764,8
			495,4	4458,6
			523,2
			385,3	4238,3
			274,2	3290,4
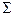
			3896,3	27142,6

Получаем:

, .

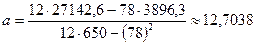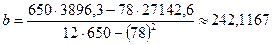Итак, уравнение функции тренда имеет вид:

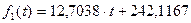Задача 13. Построить индексы сезонности за 2008 год и за 2006 – 2008 г.г. Результаты представить графически.

Помимо долговременных, на формирование значений уровней ряда динамики оказывают влияния сезонные факторы, определяющие периодическое изменение значений признака в определенные моменты времени (сезоны), причем эти изменения для каждого сезона можно считать постоянной величиной.

Самым простым способом учета сезонных факторов является расчет индексов сезонности, которые для одного года равны:

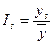Дата добавления: 2015-07-25; просмотров: 51 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Временная разность между данным и следующим уровнем.	\|	При этом - значение уровня ряда динамики в момент времени в данный момент времени (сезон) , а - среднее значение уровней ряда динамики.

mybiblioteka.su - 2015-2024 год. (0.004 сек.)