При этом - значение уровня ряда динамики в момент времени в данный момент времени (сезон) , а - среднее значение уровней ряда динамики.

Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами | В зависимости от r имеем следующую интерпретацию связи | При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные | Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной | Способ 1. Этот способ основан на проверке гипотезы о значимости коэффициента линейной корреляции с помощью t – критерия Стьюдента. | Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера. | Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации (см. задачу 9, п. 7). | С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно | Для заметок | Временная разность между данным и следующим уровнем. |

Читайте также:

С целью избежания влияния случайных факторов, на практике, расчет индексов сезонности производится не за один, а за лет. В этом случае

Где

- среднее значение уровней ряда динамики,

соответствующих определенному сезону,

Среднее значение уровней ряда динамики за лет.

После того как значения индексов сезонности рассчитаны, результаты удобно представить графически в виде ломаной с вершинами в точках с координатами(;). Также на координатной плоскости удобно изобразить линию. С ее помощью можно увидеть, в каких случаях мы имеем значения ряда динамики ниже среднего уровня, а в каких – выше.

Рассчитываем значения индексов сезонности в таблице (обратить внимание на расчет средних значений, ряд – моментный!):

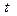
2006 г.	2007 г.	2008 г.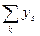

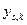
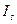
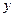
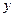
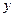
401,3	412,5	374,6	1188,4	396,1333	1,1536	1,1648
286,6	335,1	245,5	867,2	289,0667	0,7560	0,8500
332,5	348,5	304,6	985,6	328,5333	0,9380	0,9660
197,8	198,4	171,1	567,3	189,1000	0,5269	0,5560
209,7	220,8	210,8	641,3	213,7667	0,6492	0,6286
294,4		321,3	938,7	312,9000	0,9895	0,9201
	281,4	244,7	801,1	267,0333	0,7536	0,7852
329,7		345,6	1074,3	358,1000	1,0643	1,0530
476,5	531,8	495,4	1503,7	501,2333	1,5256	1,4738
503,6		523,2	1577,8	525,9333	1,6112	1,5465
408,7	428,1	385,3	1222,1	407,3667	1,1866	1,1978
341,8		274,2		299,6667	0,8444	0,8812
335,0955	360,4409	324,7182	1020,255	340,0848	-	-

Рис. 15

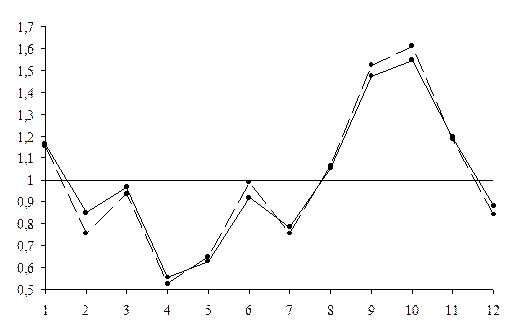Точки, соответствующие индексам сезонности, рассчитанным по данным 2008 года, соединены пунктирной линией, а трем годам – сплошной.

Задача 14. По данным о реализации продукции в 2008 году (см. задачу 11) построить математическую модель указанного ряда динамики.

С учетом долговременных и сезонных факторов, математическая модель ряда динамики представляет собой композицию функцию тренда и индексов сезонности,

Используя результаты примера 12, имеем:

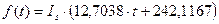Задача 15. Смоделировать ряд динамики, характеризующий объем реализации продукции в 2008 году (см. задачу 11) в виде уравнения Фурье. Число гармоник взять равным 1, 2 и 3.

Аналитическим подходом к учету сезонной и долговременной составляющих в ряде динамики, является моделирование его в виде уравнения Фурье (тригонометрического ряда):

При этом m – степень точности гармоники тригонометрического ряда; для различных значений m уравнение Фурье выглядит так (на практике берется не более четырех гармоник):

Дата добавления: 2015-07-25; просмотров: 65 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
В частности, если тренд – линейный, то	\|	Величина

mybiblioteka.su - 2015-2024 год. (0.008 сек.)