С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно

, .

Решаем задачу. Вначале, запишем эмпирические данные (объем выборки n =10) в виде таблицы:

	Y

Все необходимые расчеты осуществлены в таблице 12. Под таблицей рассчитаем средние значения, дисперсии (по формуле разностей) и средние квадратические отклонения каждого из признаков.

Таблица 12

у

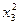
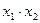
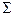
Y: , ,

, .

: , ,

, .

: , ,

, .

: , ,

, .

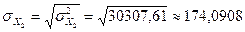Теперь найдем средние значения произведений признаков:

;

;

;

;

;

;

.

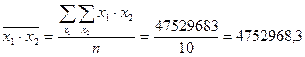Вычисляем межфакторные и парные коэффициенты линейной корреляции:

,

;

,

;

,

;

,

;

,

;

,

.

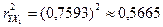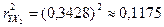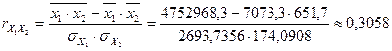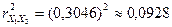Займемся отбором факторных признаков в модель.

Сначала с вероятностью 0,95 оценим статистическую значимость каждого из имеющихся факторных признаков. Согласно таблице 3 приложения критическое значение критерия Стьюдента для уровня значимости

α = 1 - 0,95 = 0,05 и числа степеней свободы ν =10 – 2 = 8 равно

.

Вычислим наблюдаемые значения:

: ;

: ;

: .

Видим, что только для признака выполняется правило проверки гипотезы. Следовательно, он однозначно включается в модель.

Между признаками и нарушается принцип отсутствия автокорреляции, , связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку > , то признак исключается из рассмотрения, а признак - остается.

Множественный коэффициент корреляции равен:

Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости.

С вероятностью 0,95 выдвинем гипотезу о статистической значимости эмпирических данных. Поскольку n = 10, k =2, то α =1-0,95 = 0,05 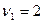, . Согласно таблице 4

.

Наблюдаемое значение равно:

.

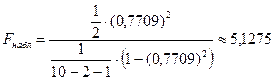Правило проверки гипотезы выполнено. Поэтому с вероятностью 0,95 гипотеза о статистической значимости эмпирических данных принимается, корреляционная модель может быть построена.

Общий индекс детерминации равен

.

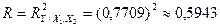Следовательно, факторные признаки, отобранные в модель, влияют на

результативный в пределах 59,43%. Это не очень сильное влияние. Согласно закону Парето степень влияния должна быть не меньше 80%.

Линейная модель, описывающая корреляционную зависимость, имеет следующий общий вид:

.

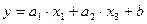Используя таблицу 12, получаем систему нормальных уравнений:

;.

Решая систему, получаем:

, , .

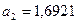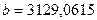Итак, искомое уравнение регрессии имеет вид:

.

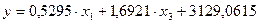Найдем параметры уравнения регрессии упрощенным способом:

,

.

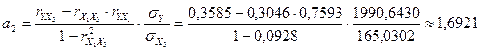Найдем среднюю ошибку аппроксимации. Для этого, подставив значения факторных признаков, соответствующих данному значению y в модель, получаем теоретические значения y*. Вычисления производим в таблице:

у
			6672,0838	0,3347
			7708,8693	0,1126
			7824,4743	0,1337
			8461,0588	0,1620
			6644,8366	0,1793
			12009,5096	0,0804
			6574,3001	0,3472
			6894,8649	0,0626
			8339,5446	0,1715
			8642,1934	0,0962
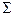
	-	-	-	1,6801

Итак, значение средней ошибки аппроксимации равно

,

что говорит о низкой точности модели.

Определим значения дельта – коэффициентов. Имеем:

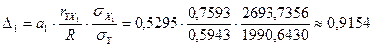или 91,54%,

или 8,46%.

Сумма дельта – коэффициентов равна 1, следовательно, есть все основания полагать, что вычисления произведены верно. Итак, признак влияет на признак Y в пределах 91,54%, а степень влияния признака равна 8,46%.

Найдем величины средних коэффициентов эластичности:

или 47,82%,

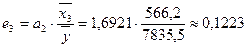или 12,23%.

Таким образом, изменение признака на 1% влечет за собой изменение признака Y на 47,82%, а вследствие изменения признака , изменение признака Y составит 12,23%

Перейдем к модели с парной регрессией. Поскольку одновременно минимум дельта – коэффициента и среднего коэффициента эластичности соответствует признаку ,

,

,

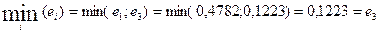то он исключается из модели. Итак, общий вид уравнения парной регрессии следующий:

.

Так как , то согласно выводам задачи 9 связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом (смотри п. 6 задачи 9): ;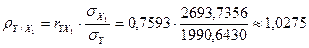

;

;

.

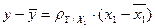Дата добавления: 2015-07-25