Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера.

Находим шаг варьирования , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности - постоянная величина. | Причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности | Где - выборочная доля (m– количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная | Для заметок | Г) если |as|<1, |es|<1 – распределение нормального типа. | Чтобы убедиться, что теоретические частоты адекватно описывают эмпирические данные, на одном чертеже строим кривую нормального распределения и полигон частот. | Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами | В зависимости от r имеем следующую интерпретацию связи | При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные | Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной |

Читайте также:

Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,

то это с доверительной вероятностью γ (уровнем значимости α =1- γ) говорит о статистической значимости эмпирических данных. При этом наблюдаемое значение критерия равно

а критическое значение критерия определяется по таблице в зависимости от уровня значимости α =1- γ и числа степеней свободы и 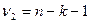(см. таблицу 4 Приложения),

5. Общий индекс детерминации позволяет определить суммарное влияние факторных признаков на результативный. Он равен:

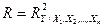6. После того, как установлена форма корреляционной зависимости, подтверждена гипотеза о статистической значимости эмпирических данных, приступают к построению многофакторной модели регрессии. Например, если модель – линейная, число факторных признаков равно двум, то ее уравнение имеет вид:

Параметры модели находятся методом наименьших квадратов путем решения системы нормальных уравнений. Например, в линейном случае для k=2, система имеет вид:

Существует другой, упрощенный способ нахождения параметров , и :

Дата добавления: 2015-07-25; просмотров: 44 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Способ 1. Этот способ основан на проверке гипотезы о значимости коэффициента линейной корреляции с помощью t – критерия Стьюдента.	\|	Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации (см. задачу 9, п. 7).

mybiblioteka.su - 2015-2024 год. (0.006 сек.)