Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации (см. задачу 9, п. 7).

Причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности | Где - выборочная доля (m– количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная | Для заметок | Г) если |as|<1, |es|<1 – распределение нормального типа. | Чтобы убедиться, что теоретические частоты адекватно описывают эмпирические данные, на одном чертеже строим кривую нормального распределения и полигон частот. | Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами | В зависимости от r имеем следующую интерпретацию связи | При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные | Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной | Способ 1. Этот способ основан на проверке гипотезы о значимости коэффициента линейной корреляции с помощью t – критерия Стьюдента. |


Читайте также:
  1. A) Потому что производится последовательная сушка зерна
  2. B тексте содержатся орфографические ошибки. Выпишите предложения с ошибками и исправьте их. Переведите текст на русский язык.
  3. ER-моделирование структуры предметной области
  4. II часть Оценка частоты встречаемости эмоций
  5. II. Оценка содержания жира (%) в организме мужчин в
  6. II. Формирование и оценка ресурсной базы кредитных организаций
  7. III. Типы семей, особенности их влияния на воспитание детей. Модели негативных семейных взаимоотношений

8. С помощью дельта – коэффициента можно ответить на вопрос: в какой мере факторный признак 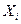влияет на результативный. Он рассчитывается по формуле:

.

Проверить правильность произведенных расчетов позволяет следующее равенство:

.

9. Величина среднего коэффициента эластичности отвечает на вопрос: на сколько процентов изменится результативный признак, если данный факторный признак 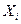изменить на 1%? Он равен:

.

Дата добавления: 2015-07-25; просмотров: 44 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера.| С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно
mybiblioteka.su - 2015-2024 год. (0.005 сек.)