Величина

.

Коэффициенты уравнения Фурье находятся по формулам:

,,.

Все необходимые вычисления осуществляем в таблицах 14, 15 и 16.

Таблица 14

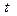
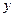
		m = 1
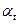
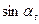
	374,6				374,6
	245,5		0,866	0,5	212,6092	122,75
	304,6		0,5	0,866	152,3	263,7913
	171,1					171,1
	210,8		-0,5	0,866	-105,4	182,5582
	321,3		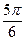-0,866	0,5	-278,254	160,65
	244,7		-1		-244,7
	345,6		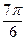-0,866	-0,5	-299,2984	-172,8
	495,4		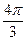-0,5	-0,866	-247,7	-429,029
	523,2			-1		-523,2
	385,3		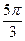0,5	-0,866	192,65	-333,6796
	274,2		0,866	-0,5	237,4642	-137,1
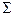
	3896,3	-	-	-	-5,7289	-694,9591

Таблица 15

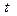
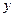
		m = 2
	374,6				374,6
	245,5		0,5	0,866	122,75	212,6092
	304,6		-0,5	0,866	-152,3	263,7913
	171,1		-1		-171,1
	210,8		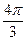-0,5	-0,866	-105,4	-182,5582
	321,3		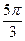0,5	-0,866	160,65	-278,2540
	244,7				244,7
	345,6		0,5	0,866	172,8	299,2984
	495,4		-0,5	0,866	-247,7	429,029
	523,2		-1		-523,2
	385,3		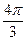-0,5	-0,866	-192,65	-333,6796
	274,2		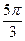0,5	-0,866	137,1	-237,4642
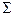
	3896,3	-	-	-	-179,75	172,7721

Таблица 16

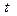
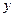
		m = 3
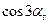
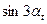
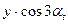
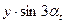
	374,6				374,6
	245,5					245,5
	304,6		-1		-304,6
	171,1			-1		-171,1
	210,8				210,8
	321,3					321,3
	244,7		-1		-244,7
	345,6			-1		-345,6
	495,4				495,4
	523,2					523,2
	385,3		-1		-385,3
	274,2			-1		-274,2
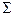
	3896,3	-	-	-	146,2	299,1

Получаем:

,

, , ,

,,.

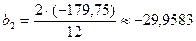Итак, уравнение Фурье в зависимости от числа гармоник имеет следующий вид:

m = 1:
m = 2:	-
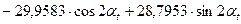
m = 3:	-
	+

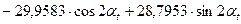Задача 16. Результаты задач 14 и 15 изобразить графически. По чертежу определить модель ряда динамики, по которой возможно построить наиболее точный прогноз.

Для того чтобы построить график функции тренда, необходимо подставить в ее уравнения значения t = 1,2, …,12. Тем самым, для каждого месяца получаем значения . Строим полученную прямую.

Чтобы получить модель ряда динамики, необходимо каждое полученное ранее значение умножить на соответствующий индекс сезонности 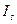. Получаем ломаную с вершинами в точках с координатами (t; ), .

Для построения графика уравнения Фурье, необходимо для каждого значения t по таблицам 14 – 16 найти значения 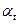, и , которые затем подставляем в уравнение. Получаем . Соединяем отрезками прямых точки с координатами (t; ). Тем самым получаем искомую ломаную.

Все необходимые вычисления удобно производить в таблице 17. Строим чертеж (рисунок 16).

Из рисунка следует, что наиболее точно описывает эмпирические данные модель Фурье, m = 3. Следовательно, по ней возможен наиболее точный прогноз.

Таблица 17

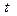
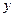
		Линейная модель	Уравнение Фурье
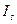
			m = 1	m = 2	m = 3
	374,6	254,8205	1,1536	293,9650	323,7368	293,7785	318,1452
	245,5	267,5244	0,7560	202,2592	265,9515	275,9098	325,7598
	304,6	280,2282	0,9380	262,8664	223,9056	263,8222	239,4556
	171,1	292,9321	0,5269	154,3513	208,8652	238,8235	188,9735
	210,8	305,6359	0,6492	198,4122	224,8604	214,9020	239,2687
	321,3	318,3397	0,9895	314,9887	267,6053	227,6886	277,5386
	244,7	331,0436	0,7536	249,4667	325,6465	295,6882	271,3215
	345,6	343,7474	1,0643	365,8530	383,4318	393,3902	343,5402
	495,4	356,4513	1,5256	543,8130	425,4778	465,3944	489,7611
	523,2	369,1551	1,6112	594,7987	440,5182	470,4765	520,3265
	385,3	381,8590	1,1866	453,1014	424,5230	414,5646	390,1980
	274,2	394,5628	0,8444	333,1785	381,7780	341,8614	292,0114

f(t)

t

Рис. 16

Задача 17. По полученным моделям ряда динамики произвести прогноз реализации продукции в магазине на январь февраль и март 2009 года.

Для того чтобы осуществить прогноз по модели ряда динамики необходимо:

Дата добавления: 2015-07-25