В бесконечной многосвязной области.

Под бесконечной многосвязной областью подразумевается плоскость, из которой удалены конечные части, ограниченные простыми замкнутыми контурами, то есть плоскость с отверстиями. Граница такой области состоит из замкнутых контуров , , …, , которые считаются по-прежнему кусочно-гладкими без точек самопересечения.

Формулы (6.7), определяющие структуру функций и в многосвязной области остаются справедливыми для любой конечной части рассматриваемой бесконечной многосвязной области . Изучим поведение функций и в окрестности бесконечно удаленной точки . Для этого опишем из точки , как из центра, окружность настолько большого радиуса 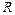, чтобы все контуры , , …, оказались внутри окружности. Для любой точки вне окружности , , где 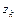– фиксированная точка внутри контура . Поэтому в окрестности точки

,

где – однозначная функция вне . Внесем полученное выражение для в формулы (6.7), придем к следующим представлениям функций и в окрестности точки :

,

. (7.1)

Здесь

,

– координаты главного вектора всех внешних нагрузок, приложенных к границе (граничным контурам , , …, ) области , а и – аналитические однозначные функции в окрестности бесконечно удаленной точки, кроме, быть может, точки

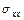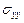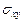Во многих конкретных задачах предполагается, что в окрестности точки напряжения , , ограничены. Выясним, какими должны быть функции и , чтобы это предположение имело место.

Согласно теореме Лорана функции и , аналитические в окрестности бесконечно удаленной точки, можно представить рядами

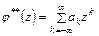, . (7.2)

Воспользуемся теперь формулами Колосова-Мусхелишвили:

,

, (7.3)

считая точку лежащей в той окрестности , в которой имеют место разложения (7.2) функций и . На основании формул (7.1), (7.2) и (7.3) получаем, что в рассматриваемой окрестности точки

.

Члены в правой части равенства, которые неограниченно возрастают по модулю при , происходят от ряда

.

Следовательно, для того, чтобы сумма осталась ограниченной при должно быть ,

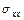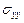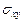Легко убедиться подобным же образом на основании формулы (7.2) и второй формулы (7.3), что для ограниченности выражения в окрестности точки необходимо, чтобы при . Верно и обратное утверждение: если для и , то напряжения , , будут ограниченными в окрестности точки .

Из сказанного выше вытекает, что в окрестности точки функции и имеют структуру

,

, (7.4)

где 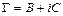, – комплексные постоянные, а , – некоторые аналитические вне функции, включая и точку , то есть имеющие в окрестности этой точки разложения вида:

, .

Выясним физический смысл постоянных 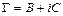и в формулах (7.4). для этого перейдем к пределу в формулах (7.3) при , будем иметь

,

.

Из этих формул вытекает, что напряжения 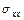, , 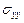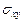стремятся к определенным пределам , , :

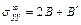, , . (7.5)

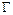Отсюда следует, что в окрестности бесконечно удаленной точки, то есть вне , распределение напряжений близко к равномерному. Из формул (7.5) получаем следующие выражения для действительных и мнимых частей постоянных и :

, , .

Постоянная остается неопределенной. Известно, что напряженное состояние тела на изменится, если функцию заменить на , где 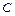– произвольная действительная постоянная, а 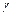– произвольная комплексная постоянная. На основании сказанного, не изменяя напряженного состояния тела, можно положить 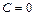. Выбором константы 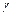можно распорядиться так, чтобы оказалось .

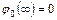Выясним поведение перемещений и при , считая по-прежнему напряжения 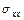, , 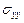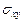ограниченными вне . Для этого воспользуемся формулой Колосова-Мусхелишвили

.

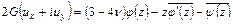Подставим в правую часть равенства выражение функций и из (7.4), получим при

.

Учитывая, что 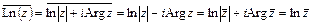, упростим полученную формулу

.

Отсюда видно, что предположение об ограниченности напряжений на бесконечности не означает, что перемещения и будут ограниченными на бесконечности. Чтобы они оставались ограниченными, должны быть соблюдены следующие условия:

, .

Первая группа условий требует, чтобы главный вектор всех внешних нагрузок, приложенных к границе области, равнялся нулю. Вторая группа условий требует, чтобы на бесконечности напряжения 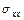, , 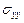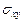равнялись нулю и, кроме того, чтобы при

.

Тело, занимающее бесконечную область, является математической идеализацией достаточно большого тела конечных размеров. Поэтому нельзя считать парадоксальным то, что в общем случае перемещения не остаются ограниченными на бесконечности в бесконечной области. На практике формулами для бесконечной области можно пользоваться только в той части тела, в которой перемещения достаточно малы.

Дата добавления: 2015-07-10