Функция напряжений.

Пусть в области 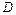переменных 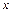и 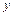заданы дифференцируемые функции и . В курсе математического анализа показано, что условие для любых является необходимым и достаточным для того, чтобы в области 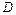существовала дважды дифференцируемая функция такая, что

, .

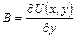Запишем уравнение равновесия (1.3) тела при плоской деформации по иному:

, , .

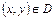Из первого уравнения следует, что в области 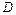, соответствующей упругому телу, существует такая функция , что

, .

Из второго уравнения равновесия вытекает, что существует функция такая, что

, .

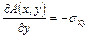Сопоставляя полученные выражения для напряжений 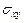, приходим к выводу, что

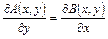
для всех точек упругого тела. Но тогда по сказанному в начале параграфа существует такая четырежды дифференцируемая в 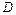функция , что

, .

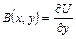Подставим полученные выражения для функций и в формулы для напряжений, получим

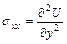, , . (2.1)

Функция называется функцией напряжений или функцией Эри (1826 г.). Формулы (2.1) означают, что любое решение уравнений равновесия плоской теории упругости может быть выражено через четырежды дифференцируемую функцию . Следовательно, решение любой граничной задачи плоской теории упругости сводится к определению соответствующей функции напряжений.

Покажем, что реальным напряжениям, возникающим в упругом теле при его деформировании, соответствует функция напряжений, удовлетворяющая бигармоническому уравнению

или . (2.2)

Здесь – оператор Лапласа:

.

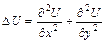Действительно, реальным напряжениям отвечают деформации 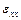, , 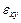(см. (1.2)), удовлетворяющие условию совместности деформаций (1.4):

.

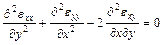Умножив обе части этого уравнения на , получим:

.

Воспользуемся теперь формулами (1.2) закона Гука, будем иметь

.

Заменив напряжения в этом равенстве на их выражения (2.1) через функцию напряжений, придем к уравнению, которому удовлетворяет функция напряжений:

.

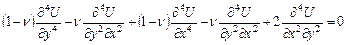После приведения подобных членов и сокращения на множитель (в теории упругости доказывается, что ) получим бигармоническое уравнение (2.2).

Любому решению бигармонического уравнения отвечают реальные напряжения в упругом теле, которые можно определить при помощи формул (2.1). Покажем, как найти перемещения 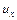и 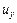точек упругого тела по известной функции напряжений .

Заменим в соотношениях (1.2) закона Гука деформации 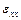, 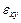их выражениями (1.1) через перемещения 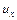и 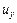, а напряжения , , 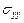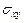согласно формулам (2.1), придем к трем равенствам:

, ,

. (2.3)

Положим . Функция является гармонической в области 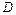, занятой телом, так как . Поэтому можно написать:

, .

Преобразуем теперь равенства (2.3) при помощи последних формул, получим:

, ,

. (2.4)

Пусть – гармоническая функция, сопряженная гармонической функции , то есть

, .

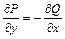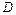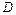Сопряженные гармонические функции и определяют в области , занятой упругим телом, аналитическую функцию комплексной переменной . Введем в области новую аналитическую функцию 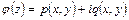, которая связана с функцией следующим образом: . Из этого равенства с учетом того, что

,

вытекают два равенства

, .

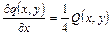Функци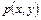и и как действительная мнимая части аналитической функции 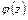удовлетворяют в области 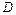условиям Коши-Римана:

, . (2.5)

Следователь, можно написать

, .

В первой и второй формулах (2.4) заменим функцию соответственно равными ей функциями и , получим тогда

, ,

.

Отсюда после интегрирования первого равенства по 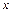, а второго по переменной 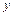, будем иметь:

,

,

.

Здесь и произвольные функции.

Подставим полученные выражения для перемещени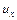й и 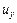в третье соотношение, получим

.

Отсюда, учитывая согласно (2.5) , приходим к следующему равенству . Это означает, что и являются противоположными константами, то есть , , где – произвольная постоянная. Очевидно,

, ,

где , – произвольные постоянные. Таким образом, оказывается, что

,

.

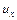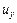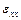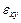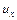Последним слагаемым в формулах для и отвечают нулевые значения деформаций , , . Это означает, что последние слагаемые соответствуют перемещениям тела без деформаций, то есть перемещениям его как твердого тела (поворот, сдвиг). Если их отбросить, тогда по известной функции напряжений перемещения и 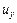упругого тела можно определить при помощи следующих формул:

,

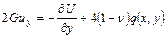. (2.6)

Опишем порядок определения перемещени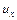й и 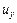упругого тела по известной функции напряжений .

1. Вычисляем производные , , , .

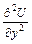2. Строим вспомогательную гармоническую функцию

.

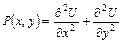3. Определяем гармоническую функцию , сопряженную функции , используя соотношения

, .

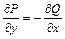4. Определяем гармонические функци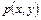и и из соотношений

, , , .

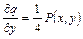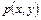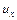5. Подставляем найденные , , и в формулы (2.6) и определяем искомые перемещения и .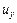

Пример. Определить перемещения в упругом теле , если .

Решение. Вычисляем производные

, , , .

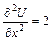Находим вспомогательную функцию :

.

Определяем вспомогательную гармоническую функцию , используя условия

, , тогда .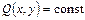

Так как требуется лишь одна функция , сопряженная , то полагаем .

Находим функци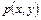и и , удовлетворяющие условиям

, , , .

Считаем , .

Вычисляем по формуле (2.6) перемещения в упругом теле

, .

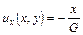Определим по формулам (2.1) также напряжения в теле

, , .

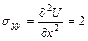Дата добавления: 2015-07-10