Читайте также:
|
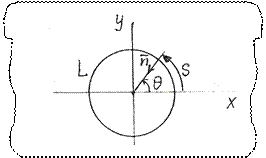
Начало декартовой системы координат поместим в центр отверстия. Будем считать известными радиус отверстия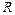 
, модули упругости 
и 
материала упругой плоскости, предельные значения напряжени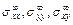й 
при 
, а также координаты 
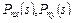вектора напряжений в произвольной точке отверстия 
(
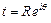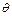есть величина угла между осью 
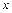и лучом, проведенным из начала координат через точку 
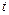). Искомыми величинами считаем напряжения 
в упругом теле.
В § 7 предыдущей темы было установлено, что искомые функции в любой окрестности точки 
и, в частности, в рассматриваемой плоскости с отверстием имеют такую структуру
,
. (3.1)
где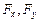 
– проекции на оси 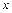и 
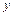главного вектора нагрузки, приложенной к контуру отверстия,
, 
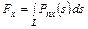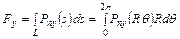; (3.2)
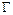и 
– комплексные постоянные:
,
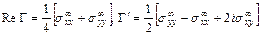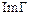– произвольная константа; 
, 
– однозначные аналитические функции в комплексной плоскости с отверстием, включая и точку , то есть имеющие разложения в ряды Лорана в окрестности этой точки вида
.
Известно, что замена функци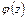й 
и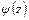 
на функции 
и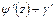 
соответственно не влияет на напряженное состояние упругого тела. Поэтому для фиксации функций 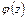, 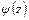можно распорядиться выбором действительной постоянной 
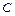и комплексных постоянных 
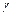и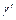 
, так, чтобы обеспечить надлежащее поведение этих функций в окрестности точки .
Функци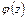и и 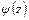на контуре 
отверстия должны удовлетворять граничным условиям (9.3), т.е.
,
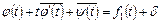где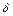 
– произвольная постоянная, 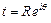– произвольная точка контура , 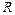– радиус отверстия,
.
Функцию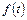 
считаем известной, так как в первой граничной задаче на границе отверстия заданы координаты 
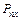и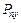 
вектора напряжения. Распорядимся выбором постоянных 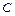, , 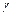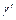так, чтобы оказалось
.
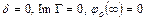В этом случае ряды Лорана для функций и в формулах (3.1) будут иметь вид:
, 
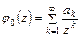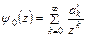. (3.4)
Преобразуем граничное условие задачи в граничное условие для функций и . На основании формул (3.1) на границе упругого тела имеем
, 
,
.
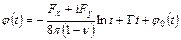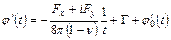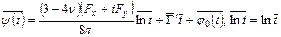Подставим эти выражения для функций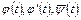 
в граничное условие задачи для функций и
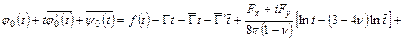
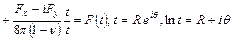. (3.5)
Предполагая, что ряды Лорана (3.4) для функций , и производные от них сходятся как во внутренних точках рассматриваемой бесконечной области, так и в точках границы и что функция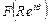 
может быть представлена комплексным рядом Фурье
,
приходим после подстановки рядов (3.4) в граничное условие (3.5) к равенству для определения коэффициентов 
и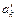 
рядов Лорана для функций и
.
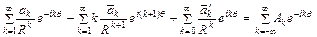После определения функций и при помощи формул (3.4), а затем и функци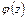й и 
при помощи формул (3.1), найдём напряжения в упругом теле, руководствуясь формулами Колосова- Мусхелишвили.
Опишем основные этапы решения первой граничной задачи плоской теории упругости для плоскости с круглым отверстием:
1. Определяем в каждой точке граничной окружности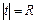 
координаты 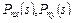вектора напряжения 
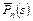по заданной нагрузке.
 |
2. Определяем напряжения 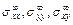по условиям нагружения плоскости с отверстием вдали от отверстия.
3. Определяем координаты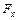 
и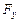 
главного вектора нагрузки, приложенного к контуру отверстия по формулам (3.2).
4. Вычисляем значения постоянных 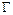и 
по формулам (3.3), которые с учетом того, что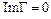 
, принимают вид:
, 
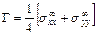. (3.7)
5. Определяем функцию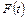 
в правой части граничного условия (3.5):
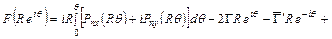
. (3.8)
6. Раскладываем функцию 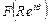в комплексный ряд Фурье
, 
.
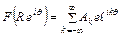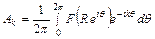7. Приравнивая коэффициенты при одинаковых степенях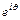 
в граничном условии (3.6), получаем уравнения для определения коэффициентов и 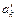рядов Лорана (3.4) для функций и .
8. По найденным функциям и строим функции 
и 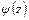, руководствуясь формулами (3.1).
Дата добавления: 2015-07-10; просмотров: 59 | Нарушение авторских прав