Читайте также:
|
Пусть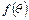 
– действительная функция, заданная на отрезке 
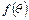и удовлетворяющая на нем условиям Дирихле (функция непрерывна на отрезке за возможным исключением конечного числа разрывов первого рода и имеет конечное число максимумов и минимумов). В этом случае функцию 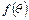можно представить рядом Фурье
,
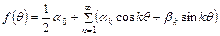где
, 
.
Напомним, что ряд Фурье сходится во всех точках интервала 
к функции 
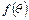, которая совпадает с в точках непрерывности. На концах 0 и 
промежутка суммой ряда оказывается число . Если 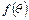является непрерывной во всех точках отрезка , удовлетворяет на нем условиям Дирихле и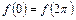 
, то ряд Фурье сходится к 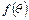равномерно на отрезке .
Заменим в ряде Фурье 
и 
известными выражениями
, 
,
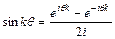получим
.
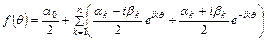После введенных новых обозначений
будем иметь
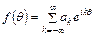. (1.1)
Этот ряд будем называть комплексным рядом Фурье функции .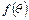
Получим выражения коэффициентов комплексного ряда через функцию 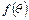. С этой целью воспользуемся тем, что для целого 
Умножим обе части формулы (1.1) на 
и проинтегрируем по 
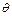от 0 до , получим:
.
Следовательно,
(1.2)
Рассмотрим теперь комплексную функцию 
, где 
и 
– действительные функции, удовлетворяющие условиям Дирихле на . Каждую из этих функций можно представить комплексным рядом Фурье вида (1.1). Умножив ряд для функции на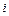 
и прибавив его к ряду для функции , получим снова ряд вида (1.1)
, (1.3)
в котором согласно (1.2)
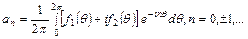(1.4)
В отличие от предыдущего случая коэффициенты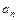 
, 
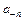ряда (1.4) не являются комплексно сопряженными числами.
Если действительная функция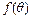 
непрерывна и имеет непрерывные производные на отрезке до порядка 
и производная порядка 
удовлетворяет условиям Дирихле на том же промежутке, то коэффициенты 
, 
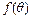ряда Фурье функции удовлетворяют неравенствам
, 
, 
,
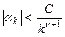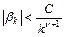где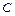 
– некоторая положительная постоянная. Отсюда вытекает, что коэффициенты 
ряда (1.3) для функции удовлетворяют неравенствам того же вида
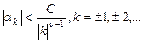
при условии, что функции и имеют непрерывные производные до порядка на , а их производные порядка удовлетворяют условиям Дирихле.
Заметим, что при 
, то есть когда функции и имеют непрерывные производные, удовлетворяющие условиям Дирихле, для коэффициентов комплексного ряда Фурье (1.3) выполняются неравенства
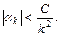
А это означает, что ряд (1.3) сходится абсолютно, так как
и ряд 
сходится.
Дата добавления: 2015-07-10; просмотров: 102 | Нарушение авторских прав