
Читайте также:
|
Обратимся к формулам (2.6) для перемещений точек упругого тела при плоской деформации. Умножим вторую формулу на 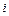 и сложим с первой формулой, получим
и сложим с первой формулой, получим
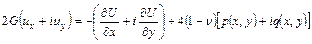 .
.
Для преобразования правой части равенства воспользуемся формулой (3.2) для 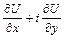 и тем, что
и тем, что 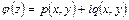 . Тогда придем к следующему комплексному представлению перемещений
. Тогда придем к следующему комплексному представлению перемещений
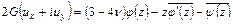 , (4.1)
, (4.1)
где 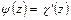 – аналитическая функция в области
– аналитическая функция в области  , занятой телом.
, занятой телом.
Рассмотрим теперь линейные комбинации напряжений 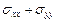 и
и 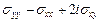 . Согласно формулам (2.1), (3.3), (3.4), используя функции
. Согласно формулам (2.1), (3.3), (3.4), используя функции 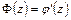 и
и 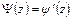 , получаем
, получаем
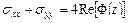 ,
,
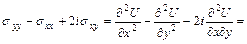
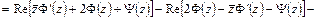
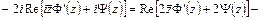
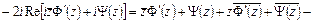
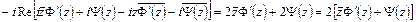 .
.
Таким образом,
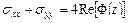 , (4.2)
, (4.2)
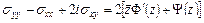 . (4.3)
. (4.3)
В этих формулах
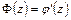 ,
, 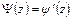 ,
, 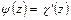 . (4.4)
. (4.4)
Формулы (4.1)-(4.3) называются формулами Колосова-Мусхелишвили. Из этих формул вытекает, что для определения напряжений и перемещений в упругом теле достаточно найти две аналитические функции  и
и  в области, занятой телом. Если же требуется определить только напряжения в теле, то для этого достаточно найти две аналитические функции
в области, занятой телом. Если же требуется определить только напряжения в теле, то для этого достаточно найти две аналитические функции 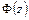 и
и 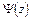 .
.
Поясним механический смысл функции
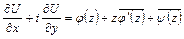 .
.
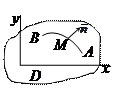 Пусть
Пусть  – область, занятая упругим телом, а
– область, занятая упругим телом, а 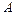 и
и 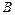 – две различные точки этой области. Соединим эти точки какой-либо гладкой дугой. Установим на ней положительное направление от точки
– две различные точки этой области. Соединим эти точки какой-либо гладкой дугой. Установим на ней положительное направление от точки 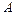 к точке
к точке 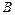 . Так как дуга гладкая, то с каждой ее точкой можно связать единичный вектор
. Так как дуга гладкая, то с каждой ее точкой можно связать единичный вектор 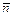 , нормальный к касательной (единичный нормальный вектор). Считаем, что вектор
, нормальный к касательной (единичный нормальный вектор). Считаем, что вектор 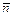 направлен вправо, если двигаться по дуге в положительном направлении.
направлен вправо, если двигаться по дуге в положительном направлении.
Отбросим часть тела, расположенную справа от дуги 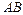 , и заменим действие отброшенной части тела на оставшуюся нагрузками, распределенными вдоль дуги
, и заменим действие отброшенной части тела на оставшуюся нагрузками, распределенными вдоль дуги 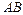 . Обозначим через
. Обозначим через 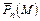 – вектор напряжения в точке
– вектор напряжения в точке 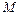 дуги по сечению с внешней нормалью
дуги по сечению с внешней нормалью 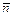 . Тогда, очевидно, интеграл
. Тогда, очевидно, интеграл
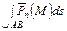
будет главным вектором 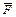 распределенной по дуге нагрузки. Пусть
распределенной по дуге нагрузки. Пусть 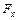 и
и 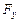 проекции вектора
проекции вектора 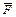 на оси
на оси 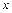 и
и 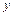 соответственно. Тогда, как показано в монографии [],
соответственно. Тогда, как показано в монографии [],
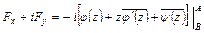 . (4.5)
. (4.5)
В правой части равенства стоит разность значений функции 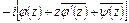 в точках
в точках 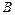 и
и 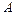 .
.
§ 5. Степень определенности функций 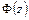 ,
, 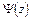 ,
,  и
и  .
.
Предположим, что напряжения 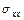 ,
, 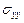 ,
, 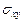 в упругом теле
в упругом теле  известны. Эти напряжения выражаются через две аналитические в
известны. Эти напряжения выражаются через две аналитические в  функции
функции 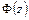 и
и 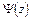 согласно формулам (4.2) и (4.3). Возникает вопрос: являются ли указанные функции единственными для данного напряженного состояния тела?
согласно формулам (4.2) и (4.3). Возникает вопрос: являются ли указанные функции единственными для данного напряженного состояния тела?
Предположим, что кроме совокупности аналитических функций 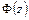 ,
, 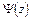 ,
, 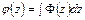 ,
, 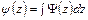 , существует другая совокупность аналитических функций
, существует другая совокупность аналитических функций 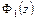 ,
, 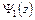 ,
, 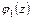 и
и 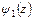 , которой отвечают такие же напряжения в теле, как и первой совокупности аналитических функций. Тогда
, которой отвечают такие же напряжения в теле, как и первой совокупности аналитических функций. Тогда
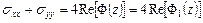 ,
,
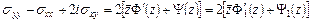 ,
,
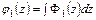 ,
, 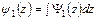 . (5.1)
. (5.1)
Из этих равенств видно, что аналитические функции 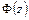 и
и 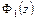 имеют одинаковые действительные части. Отсюда следует, что разность
имеют одинаковые действительные части. Отсюда следует, что разность 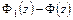 есть комплексная константа вида
есть комплексная константа вида 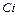 , где
, где 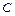 – действительной число. Действительно, пусть
– действительной число. Действительно, пусть 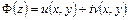 , а
, а 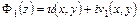 . Согласно условиям Коши-Римана имеем
. Согласно условиям Коши-Римана имеем
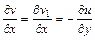 ,
, 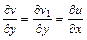 .
.
Частные производные функций 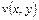 и
и 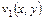 по переменной
по переменной 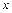 одинаковы. Одинаковы и частные производные этих функций по переменой
одинаковы. Одинаковы и частные производные этих функций по переменой 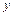 . Следовательно,
. Следовательно, 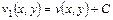 и, потому,
и, потому, 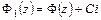 . Из последнего равенства вытекает, что первообразные функций
. Из последнего равенства вытекает, что первообразные функций 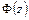 и
и 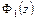 отличаются на слагаемое вида
отличаются на слагаемое вида 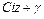 , где
, где 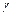 – произвольная комплексная постоянная, то есть
– произвольная комплексная постоянная, то есть
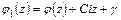 .
.
Поскольку 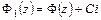 , то
, то 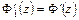 , но тогда из (5.1) следует, что в области
, но тогда из (5.1) следует, что в области 
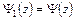 , а
, а 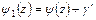 .
.
Таким образом, заданному напряженному состоянию тела отвечает не единственный набор функций 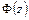 ,
, 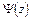 ,
,  и
и  , а класс наборов, при этом два различных набора связаны соотношениями
, а класс наборов, при этом два различных набора связаны соотношениями
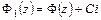 ,
, 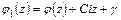 ,
,
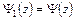 ,
, 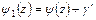 . (5.2)
. (5.2)
Здесь, 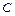 – действительная постоянная,
– действительная постоянная, 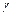 и
и 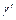 – комплексные постоянные.
– комплексные постоянные.
Выясним теперь, как различаются наборы функций 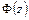 ,
, 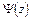 ,
,  ,
,  , отвечающие заданным напряжениям
, отвечающие заданным напряжениям 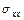 ,
, 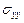 ,
, 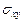 и перемещениям
и перемещениям  и
и  в теле, то есть отвечающие заданному напряженно-деформированному состоянию тела. Пусть кроме функций
в теле, то есть отвечающие заданному напряженно-деформированному состоянию тела. Пусть кроме функций 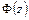 ,
, 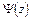 ,
,  ,, которым соответствуют заданные в теле напряжения и перемещения, существуют еще функции
,, которым соответствуют заданные в теле напряжения и перемещения, существуют еще функции 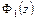 ,
, 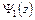 ,
, 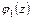 ,
, 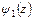 , которым отвечают те же напряжения и перемещения в теле. Тогда в области
, которым отвечают те же напряжения и перемещения в теле. Тогда в области  должны выполняться равенства (5.1) и равенства
должны выполняться равенства (5.1) и равенства
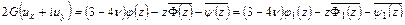 . (5.3)
. (5.3)
Как было установлено выше, из равенств (5.1) вытекают соотношения (5.2) между рассматриваемыми двумя наборами функций. Равенства (5.3) накладывают дополнительные ограничения на выбор постоянных 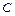 ,
, 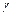 и
и 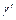 , а именно
, а именно
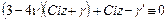 .
.
Учитывая, что в левой части тождества находится многочлен первой степени относительно переменной  , приходим к выводу:
, приходим к выводу:
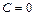 ,
, 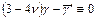 . (5.4)
. (5.4)
Следовательно, два каких-либо набора функций, отвечающих одному и тому же напряженно-деформированному состоянию упругого тела связаны такими соотношениями
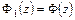 ,
, 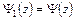 ,
, 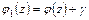 ,
, 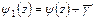 ,
,
причем комплексные постоянные 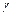 и
и 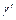 не являются произвольными, а удовлетворяют условию (5.4).
не являются произвольными, а удовлетворяют условию (5.4).
произвольными постоянными, с точностью до которых определяются искомые функции 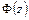 ,
, 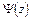 ,
,  ,
,  , можно всегда распорядиться так, чтобы эти функции приняли наиболее простой вид.
, можно всегда распорядиться так, чтобы эти функции приняли наиболее простой вид.
Дата добавления: 2015-07-10; просмотров: 837 | Нарушение авторских прав