
Читайте также:
|
Из результатов предыдущего параграфа можно сделать вывод о том, что решение любой граничной задачи плоской теории упругости, то есть задачи об отыскании такого решения системы дифференциальных уравнений (1.1)-(1.3), которое удовлетворяет заданным граничным условиям в области, занятой телом, сводится к отысканию лишь одной бигармонической функции напряжений  . Можно еще более упростить решение задачи плоской теории упругости, сведя их к определению двух аналитических функций в области, занятой упругим телом. Покажем это.
. Можно еще более упростить решение задачи плоской теории упругости, сведя их к определению двух аналитических функций в области, занятой упругим телом. Покажем это.
Пусть  – некоторая бигармоническая функция. С этой функцией связываем гармоническую функцию
– некоторая бигармоническая функция. С этой функцией связываем гармоническую функцию
 .
.
При помощи функции  построим пару сопряженных гармонических функций
построим пару сопряженных гармонических функций 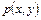 и
и  , которые определяют аналитическую функцию
, которые определяют аналитическую функцию 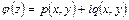 в области
в области  , занятой упругим телом. Пусть
, занятой упругим телом. Пусть  –функция, сопряженная
–функция, сопряженная  , положим
, положим
 .
.
Рассмотрим функцию  . Подействуем на нее оператором Лапласа, получим
. Подействуем на нее оператором Лапласа, получим

 ,
,
так как  . Следовательно, функция
. Следовательно, функция  является гармонической в области
является гармонической в области  . Таким образом, произвольная бигармоническая функция
. Таким образом, произвольная бигармоническая функция  может быть представлена в виде
может быть представлена в виде
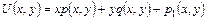 ,
,
где 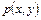 и
и  – сопряженные гармонические функции, а
– сопряженные гармонические функции, а  – гармоническая функция.
– гармоническая функция.
Введем в рассмотрение аналитическую функцию
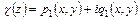 ,
,
тогда предыдущее выражение для бигармонической функции  можно записать в таком виде
можно записать в таком виде
 , (3.1)
, (3.1)
где  – действительная часть комплексного числа
– действительная часть комплексного числа  ,
,  ,
,  ,
, 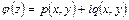 . Полученная формула определяет искомое представление бигармонической функции
. Полученная формула определяет искомое представление бигармонической функции  через две аналитические функции
через две аналитические функции  и
и  .
.
Для определения напряжений и перемещений в упругом теле важно знать не столько функцию напряжений, сколько ее производные по переменным 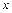 и
и 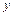 . Вычислим первые и вторые производные функции напряжений (3.1). Имеем
. Вычислим первые и вторые производные функции напряжений (3.1). Имеем

 .
.
Аналогично
 .
.
Воспользуемся тем, что для любого комплексного числа  верно равенство:
верно равенство:
 .
.
Тогда можно написать
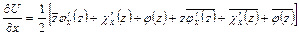 ,
,
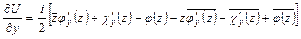 .
.
Удобно в приложениях рассматривать комплексную комбинацию первых производных функции напряжения
 . (3.2)
. (3.2)
Вычислим теперь вторые производные от функции  . Имеем
. Имеем
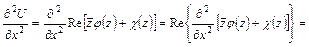
 ,
,
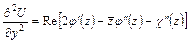 ,
,

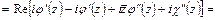
 . (3.3)
. (3.3)
Из полученных выражений для вторых производных функции напряжения вытекает, что
 . (3.4)
. (3.4)
Дата добавления: 2015-07-10; просмотров: 153 | Нарушение авторских прав