Основные граничные задачи плоской теории упругости.

В недеформированном упругом теле напряжения 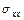, , 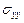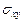и деформации 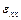, , 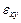равны нулю. Если же тело деформировано заданными нагрузками, которые считаем приложенными к его границе, то ясно, что в упругом теле будут отличными от нуля напряжения, деформации и перемещения , . Задачу об определении величин 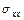, , 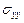, , 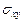, , 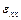, 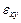во всех точках упругого тела при заданных напряжениях на его границе будем называть первой граничной задачей. Во второй граничной задаче на всей границе тела считаются заданными перемещения , ; искомыми величинами по-прежнему являются напряжения, перемещения и деформации в упругом теле. В смешанной граничной задаче на части границы тела заданы напряжения, а на оставшейся части перемещения.

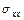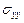Если область , соответствующая упругому телу, конечна, то решение трех сформулированных задач единственно [] (в предположении, что все граничные контуры гладкие и что напряжения и перемещения непрерывны в замкнутой области , занятой упругим телом). Если же область бесконечна, то для единственности решения первой граничной задачи нужно дополнительно задать значения напряжений , , на бесконечности []. Перемещения , точек тела в первой граничной задаче определяются с точностью до слагаемых вида

, ,

которые соответствуют жесткому перемещению тела в плоскости . На основании сказанного в §7 задание напряжений на бесконечности эквивалентно заданию постоянных и в формулах (7.4). Так как постоянная не влияет на распределение напряжений в теле, то будем полагать 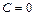. В случае второй граничной задачи и смешанной задачи для бесконечного тела требование единственности решения будет выполнено, если дополнительно задать значения напряжений на бесконечности, главный вектор всех усилий и

.

Задание этих величин эквивалентно заданию постоянных []

, , ,

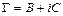в формулах (7.4).

Пример. Записать граничные условия в задаче о растяжении плоскости с круглым отверстием усилиями на бесконечности интенсивности (кг/см). Радиус отверстия 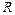(см). на границу отверстия действует равномерно распределенная нормальная нагрузка интенсивности 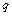(кг/см).

Решение. Вычисли вектор напряжения 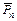в точке 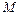границы тела. Здесь 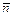– единичный вектор внешней нормали. Пусть точка 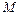характеризуется дуговой координатой (см. рис.). На малый участок границы с центром в точке 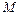длиной действует нагрузка, главный вектор которой направлен к центру окружности, то есть 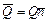. Величина главного вектора . Это приближенное равенство тем точнее, чем меньше (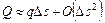). По определению

.

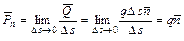Как видно из рисунка, для любых значений дуговой координаты

, .

Следовательно, координаты вектора 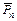равны

, .

Во всех точках границы рассматриваемого тела известны нормальные нормальное и касательное напряжения

, =0.

Поэтому сформулированная задача теории упругости для бесконечной плоскости является первой.

Определим напряжения , , . Введем вспомогательную систему координат с осями , . Ось направим параллельно линям действия усилий 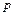, которые растягивают тело на бесконечности (см. рис.). В точке тела, лежащей в окрестности бесконечно удаленной точки, имеем

.

Следовательно, , .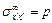

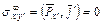Проведем через точку сечение, перпендикулярное оси и отбросим ту часть тела, внутри которой направлен вектор . По смыслу задачи на малую окрестность точки со стороны отброшенной части нагрузка не действует, поэтому . Следовательно, , .

Вычислим теперь напряжения , , , используя найденные значения напряжений , , 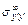. Для этого воспользуемся известными формулами связи между напряжениями в одной и той же точке тела, вычисленными в различных двух правых декартовых системах координат [; гл. 4]:

,

,

.

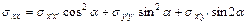Здесь – угол между осью и осью 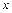(положительное направление отсчета угла против хода часовой стрелки). В рассматриваемом случае 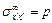, , , . Следовательно,

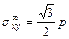, , . (8.2)

Условия (8.1) и (8.2) обеспечивают единственность решения рассматриваемой задачи теории упругости.

Дата добавления: 2015-07-10