Основные определения и положения теории упругости.

Министерство образования и науки Украины

Запорожский национальный университет

А.К. Приварников

Методическое пособие по курсу

«ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ»

Для студентов-магистров специальности «математика» математического факультетов

ЗАПОРОЖЬЕ

ЗНУ 2008

Основные определения и положения теории упругости.

Тело называется упругим, если после снятия приложенных к нему нагрузок оно восстанавливает свою первоначальную форму.

Пусть 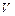– упругое тело. Введем в пространстве правую декартовую систему координат с осями 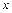, , . Пусть – некоторая точка тела 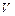. После деформации тела точка 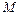займет положение 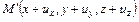. Вектор называется вектором перемещения точки 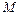, а его координаты называются перемещениями точки 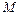в направлении осей 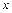, , 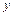. Перемещения , , являются функциями переменных 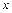, , 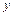, эти функции определены в области .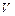

Пусть точка – точка деформированного тела . Отложим из этой точки единичный вектор 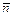и проведем через точку 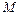сечение, перпендикулярное вектору 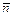. Отбросив ту часть тела, внутрь которой направлен вектор 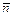. действие отброшенной части тела на оставшуюся заменим соответствующими силами.

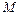Выделим малую окрестность , содержащую точку . Ее площадь обозначим через . Пусть – главный вектор сил, приложенных к окрестности . Вектор называется средним напряжением в окрестности , а называется напряжением в точке 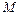тела по сечению с вектором нормали .

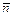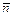Проекция вектора напряжения на вектор нормали называется нормальным напряжением в точке 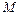по сечению с нормалью 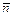. Проекция вектора на секущую плоскость называется касательным напряжением.

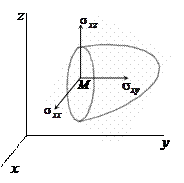Проведем через точку 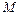сечение перпендикулярно вектору (направляющий вектор оси 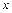). Вектор напряжения в точке 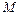будем обозначать .

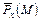Проекции вектора на оси 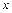, , 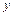обозначаются , , соответственно и называются нормальными напряжениями ( ) и касательными напряжениями ( , ). Так как координаты вектора равны проекциям этого вектора на оси 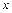, , 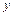, то .

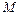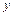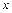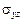Поведем теперь через точку сечение, перпендикулярное оси , и спроектируем вектор на оси y, , , получим – нормальное напряжение, и – касательные напряжения. Ясно, что .

Если провести через точку 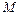сечение перпендикулярно оси и спроектировать вектор 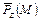на оси 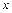, , 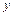, получим 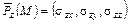, где , – касательные напряжения, – нормальное напряжение.

Матрица

называется тензором напряжений в точке .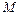

В теории упругости (ТУ) доказано, что координаты вектора можно вычислить по известным координатам вектора 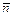при помощи следующих формул:

,

,

.

Пример. Тензор напряжений 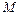в точке . Вычислить длину вектора напряжения в точке 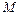по сечению, которое перпендикулярно биссектрисе координатного угла .

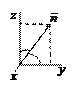Решение. Очевидно, что 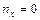, , . Координаты вектора найдем по формуле:

.

Тогда

.

Найдем длину вектора : (Н/м²).

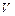Предположим, что известны перемещения , , во всех точках тела . Тогда можно вычислить следующие величины:

, , , ,

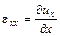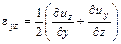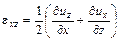, . (0.1)

Эти величины называются деформациями, а матрица 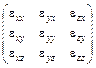называется тензором деформаций. Тензор деформаций является симметричной матрицей. Симметричной матрицей является и тензор напряжений.

Если считать известными деформации в теле и пытаться определить соответствующие им перемещения, то для решения этой задачи нужно решить шесть уравнений (0.1) относительно трех неизвестных , , . Это будет возможным, если система уравнений окажется совместной. Условия совместноcти деформаций, то есть условия совместности системы (0.1) имеют вид:

, ,

, ,

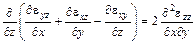, . (0.2)

Если к упругому телу 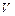приложить нагрузку, то оно деформируется: в нем возникнут напряжения, деформации и перемещения. Это означает, что должна существовать связь между деформациями и напряжениями. Для однородного, изотропного, упругого тела эта связь определяется законом Гука:

, ,

, ,

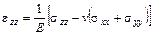, , (0.3)

где – модуль Юнга, – коэффициент Пуассона, – модуль сдвига.

Коэффициент Пуассона не превосходит 0,5 и является положительным. Для резины , для стали, меди, алюминия 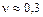, для пробки . Приведем значение модуля Юнга для некоторых материалов. Для стали № 3 кг/см² Н/м², для меди 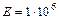кг/см² 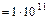Н/м², для алюминия 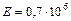кг/см² Н/м².

Для уяснения сути понятия «модуль Юнга» приведем следующую формулу:

– удлинение стержня при деформации.

Здесь – площадь поперечного сечения стержня; – удлинение стержня при деформации; – первоначальная длина стержня; – модуль Юнга материала стержня.

В задачах ТУ искомыми величинами считаются шесть компонент тензора напряжений 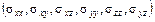, шесть компонент тензора деформаций 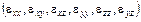, три компоненты вектора смещения в каждой точке. Всего неизвестных величин 15. для их определения используют полную систему уравнений ТУ, которая состоит из следующих систем уравнений:

1. Уравнения равновесия:

,

,

.

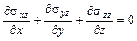2. Закон Гука (0.3).

3. Соотношения Коши (0.1).

4. Условия совместности деформаций (0.2).

Любая задача теории упругости заключается в отыскании такого частного решения полной системы уравнений ТУ, которая удовлетворяет граничным условиям на поверхности тела. Например, если в каждой точке поверхности тела известны величины , , , то задача об определении напряжений, перемещений и деформаций в теле называется второй граничной задачей ТУ. Если во всех точках поверхности тела известны нормальные и касательные напряжения и требуется найти 15 указанных неизвестных величин, то такая задача ТУ считается первой граничной задачей ТУ. Если на части поверхности тела известны напряжения, а на оставшейся части – перемещения, то граничную задачу ТУ называют смешанной граничной задачей ТУ.

Дата добавления: 2015-07-10