Основные уравнения плоской теории упругости.

Рассмотрим упругое тело, которое является или прямой призмой или прямым цилиндром с произвольной направляющей. Основания призмы или цилиндра параллельны друг другу и перпендикулярны боковой поверхности. Отнесем упругое тело к ПДСК. Плоскость 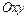параллельна основаниям тела, а ось перпендикулярна основаниям. 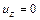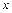Деформация рассматриваемого тела называется плоской, если для всех точек тела перемещение , а перемещения и являются функциями лишь переменных и 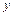. Это означает, что при плоской деформации тела под действием приложенных к нему нагрузок точки тела перемещаются параллельно плоскости 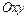при этом точки, расположенные на прямой, параллельной оси , имеют одинаковые перемещения.

Зная перемещения 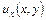, , 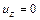точек тела, можно по формулам Коши вычислить деформации:

, , , ,

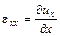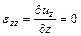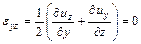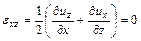, . (1.1)

По известным деформациям можно определить напряжения в упругом теле при помощи закона Гука:

, ,

, , , .

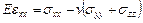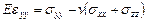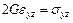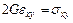Здесь – модуль Юнга, – коэффициент Пуассона, – модуль сдвига материала тела, которое считается однородным и изотропным. Принимаем во внимание, что при плоской деформации тела 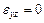, , 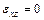, 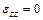приходим к выводу, что 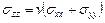, , 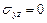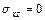. Воспользуемся установленными фактами относительно деформаций и напряжений, чтобы записать соотношения закона Гука для случая плоской деформации упругого тела:

, ,

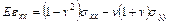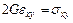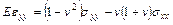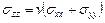, . (1.2)

Из этих формул следует, что не равные тождественно нулю напряжения 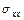, , 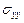, 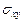в упругом теле не зависят от переменной .

Полная система уравнений плоской теории упругости, кроме соотношений Коши (1.1) и закона Гука (1.2), включает в себя дифференциальные уравнения равновесия упругого тела и условия совместности деформаций. В общем случае уравнения равновесия тела при отсутствии объемных сил имеют вид

, ,

, ,

, .

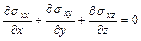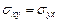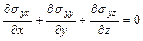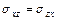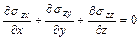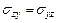При плоской деформации тела напряжения 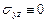, , 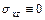а остальные напряжения являются функциями переменных 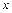и 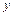. Поэтому уравнения равновесия тела при плоской деформации имеют более простой вид

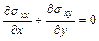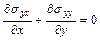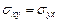, , . (1.3)

Из шести условий совместности деформаций [] при плоской деформации тела пять тождественно удовлетворяются, а оставшееся условие принимает вид:

. (1.4)

Уравнения (1.1)–(1.4) образуют полную систему уравнений плоской теории упругости для плоской деформации тела. Искомыми величинами являются напряжения 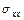, , 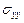, , 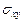деформации 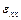, , 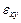и перемещения , .

Для однозначного определения искомых величин в упругом теле из полной системы дифференциальных уравнений плоской теории упругости ее нужно дополнить граничными условиями для точек поверхности тела. Если на боковой поверхности тела заданы нормальные и касательные напряжения, то задача об определении искомых величин называется первой граничной задачей плоской теории упругости. Если на боковой поверхности тела заданы перемещения и , то имеем вторую граничную задачу. Если же на части боковой поверхности заданы перемещения, а на оставшейся – напряжения, то граничную задачу плоской теории упругости называют смешанной.

Искомые величины в любой граничной задаче плоской теории упругости не зависят от переменной . Поэтому задаваемые на боковой поверхности тела напряжения или перемещения также не зависят от переменной . Следовательно, чтобы указать способ нагружения тела достаточно это сделать для одного поперечного сечения.

Дата добавления: 2015-07-10