
Читайте также:
|
По физическому смыслу напряжения и перемещения в упругом теле являются однозначными функциями независимо от того, является ли область  , занятая телом, односвязной или многосвязной. Этого нельзя сказать об искомых аналитических в
, занятая телом, односвязной или многосвязной. Этого нельзя сказать об искомых аналитических в  функциях
функциях 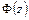 ,
, 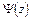 ,
,  ,
,  .
.
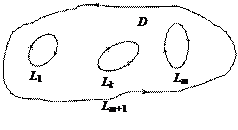 Пусть область
Пусть область  ограничена конечным числом замкнутых контуров
ограничена конечным числом замкнутых контуров  ,
,  , …,
, …,  ,
,  , не имеющих общих точек. Пусть контур
, не имеющих общих точек. Пусть контур  охватывает все остальные. Любой контур считаем гладким или кусочно-гладким. На каждом из контуров установим положительное направление обхода области
охватывает все остальные. Любой контур считаем гладким или кусочно-гладким. На каждом из контуров установим положительное направление обхода области  : при движении по контуру
: при движении по контуру  в положительном направлении область
в положительном направлении область  остается слева.
остается слева.
Рассмотрим одну из формул Колосова-Мусхелишвили:
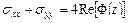 .
.
По физическому смыслу напряжения 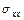 и
и 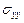 являются однозначными функциями в области
являются однозначными функциями в области  . Следовательно, действительная часть аналитической функции
. Следовательно, действительная часть аналитической функции 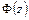 также является однозначной функцией точек области
также является однозначной функцией точек области  . Мнимая же часть
. Мнимая же часть 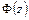 в общем случае может оказаться многозначной функцией. Это означает, что при обходе одного или нескольких контуров
в общем случае может оказаться многозначной функцией. Это означает, что при обходе одного или нескольких контуров  ,
,  , …,
, …,  значение функции может изменяться и не совпадать с исходным.
значение функции может изменяться и не совпадать с исходным.
Пусть при обходе контура  функция
функция 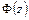 получает приращение
получает приращение 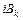 , где
, где 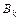 – действительная постоянная. введем вместо
– действительная постоянная. введем вместо 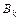 более удобную для последующего постоянную
более удобную для последующего постоянную 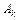 :
:
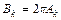 ,
,  .
.
Рассмотрим вспомогательную функцию в 
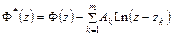 , (6.1)
, (6.1)
где 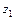 ,
, 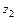 , …,
, …, 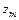 – некоторые фиксированные точки комплексной плоскости, выбранные внутри контуров
– некоторые фиксированные точки комплексной плоскости, выбранные внутри контуров  ,
,  , …,
, …,  . Учитывая формулу
. Учитывая формулу
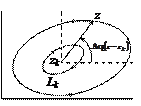
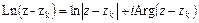 ,
,
заключаем, что при однократном обходе контура  против часовой стрелки по любой замкнутой кривой функция
против часовой стрелки по любой замкнутой кривой функция 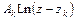 получит приращение
получит приращение 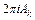 . Остальные члены под знаком суммы в формуле (6.1) приращения не получат. Это означает, что функция
. Остальные члены под знаком суммы в формуле (6.1) приращения не получат. Это означает, что функция 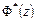 оказывается я однозначной в области
оказывается я однозначной в области  . Таким образом, искомая функция
. Таким образом, искомая функция 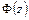 имеет такую структуру:
имеет такую структуру:
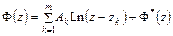 , (6.2)
, (6.2)
где 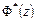 – однозначная в
– однозначная в  аналитическая функция.
аналитическая функция.
Рассмотрим функцию  . Известно, что эта функция связана с функцией
. Известно, что эта функция связана с функцией 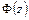 таким соотношением
таким соотношением
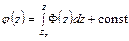 ,
,
где  – произвольная точка области
– произвольная точка области  , а
, а  – некоторая фиксированная точка той же области. Принимая во внимание формулу (6.2), получаем:
– некоторая фиксированная точка той же области. Принимая во внимание формулу (6.2), получаем:
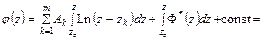
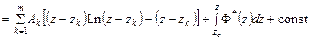 .
.
Но интеграл
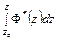
представляет собой функцию комплексного переменного  в многосвязной области
в многосвязной области  , которая при обходе вокруг одно из контуров
, которая при обходе вокруг одно из контуров  может получить приращение
может получить приращение 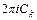 , где
, где  – в общем случае комплексная постоянная (например,
– в общем случае комплексная постоянная (например, 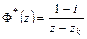 ). Поэтому, аналогично предыдущему можно написать
). Поэтому, аналогично предыдущему можно написать
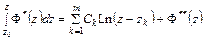 ,
,
где 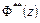 – однозначная в
– однозначная в  функция. Внесем полученное выражение для интеграла в последнюю формулу для
функция. Внесем полученное выражение для интеграла в последнюю формулу для  . после очевидных преобразований приведем выражение для функции
. после очевидных преобразований приведем выражение для функции  к виду:
к виду:
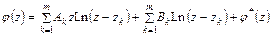 . (6.3)
. (6.3)
Установим теперь характер многозначности функции 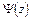 и
и  . Для этого воспользуемся следующей формулой Колосова-Мусхелишвили
. Для этого воспользуемся следующей формулой Колосова-Мусхелишвили
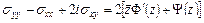 .
.
Слева в этом равенстве стоит однозначная функция точек области  , следовательно, функция
, следовательно, функция 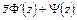 также однозначна в
также однозначна в  . Из формулы (6.2) вытекает однозначность функции
. Из формулы (6.2) вытекает однозначность функции 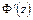 . Функция
. Функция 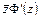 однозначна в
однозначна в  как произведение двух однозначных функций. Следовательно, функция
как произведение двух однозначных функций. Следовательно, функция 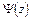 является однозначной в многосвязной области
является однозначной в многосвязной области  . Функция
. Функция
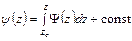
может оказаться многозначной, так при обходе вокруг контура  интеграл может получить в общем случае ненулевое приращение. Таким образом, в общем случае функция
интеграл может получить в общем случае ненулевое приращение. Таким образом, в общем случае функция  имеет такую структуру в
имеет такую структуру в  :
:
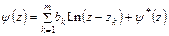 , (6.4)
, (6.4)
где 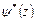 – однозначная в
– однозначная в  функция.
функция.
Учтем теперь то обстоятельство, что перемещения  и
и  по физическому смыслу являются однозначными функциями точек области
по физическому смыслу являются однозначными функциями точек области  . Но тогда однозначна в
. Но тогда однозначна в  и функция
и функция 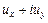 . Воспользуемся третьей формулой Колосова-Мусхелишвили:
. Воспользуемся третьей формулой Колосова-Мусхелишвили:
 .
.
Отправляясь от формул (6.2)-(6.4), выразим приращение правой части последнего равенства через постоянные 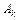 ,
, 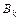 и
и 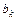 при однократном обходе контура
при однократном обходе контура  (приращение левой части равно нулю)
(приращение левой части равно нулю)
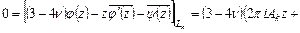
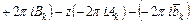 .
.
Это равенство выполняется для произвольно взятого  , поэтому коэффициенты многочлена первой степени относительно переменной
, поэтому коэффициенты многочлена первой степени относительно переменной  (в правой части равенства) должны быть равны нулю, то есть
(в правой части равенства) должны быть равны нулю, то есть
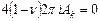 ,
, 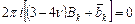 .
.
Отсюда вытекает, что
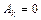 ,
, 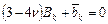 . (6.5)
. (6.5)
В § 4 указывалось, что координаты 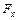 и
и 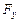 главного вектора нагрузки, которая приложена к дуге
главного вектора нагрузки, которая приложена к дуге 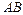 со стороны отброшенной части тела, можно вычислить при помощи формулы:
со стороны отброшенной части тела, можно вычислить при помощи формулы:
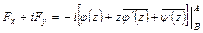 .
.
Возьмем в качестве дуги 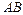 какой-либо контур
какой-либо контур 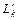 , охватывающий контур
, охватывающий контур  и не охватывающий других граничных контуров области
и не охватывающий других граничных контуров области  . При обходе этого контура по ходу часовой стрелки (по ходу часовой стрелки совершается обход и контура
. При обходе этого контура по ходу часовой стрелки (по ходу часовой стрелки совершается обход и контура  в положительном направлении) получим
в положительном направлении) получим
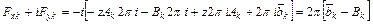 . (6.6)
. (6.6)
Правая часть этого равенства является постоянной величиной и, поэтому, не зависит от выбора контура 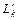 , который можно взять как угодно близким к граничному контуру
, который можно взять как угодно близким к граничному контуру  . Это дает основание считать
. Это дает основание считать  и
и  координатами главного вектора внешней нагрузки, приложенного к контуру
координатами главного вектора внешней нагрузки, приложенного к контуру  .
.
На равенства (6.5) и (6.6) можно смотреть как на систему уравнений относительно неизвестных постоянных 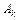 ,
, 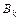 и
и 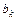 . Из этой системы находим
. Из этой системы находим
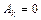 ,
, 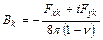 ,
, 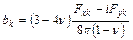 .
.
Подставим полученные значения постоянных 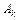 ,
, 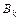 ,
, 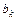 в формулы (6.3) и (6.4), получим окончательное выражение для функций
в формулы (6.3) и (6.4), получим окончательное выражение для функций  и
и  :
:
 ,
,
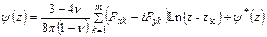 . (6.7)
. (6.7)
Здесь 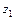 ,
, 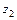 , …,
, …, 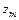 – произвольно выбранные точки, расположенные внутри контуров
– произвольно выбранные точки, расположенные внутри контуров  ,
,  , …,
, …,  ;
; 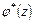 ,
, 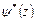 – однозначные аналитические в многосвязной области
– однозначные аналитические в многосвязной области  функции;
функции;  ,
, 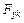 – координаты главного вектора внешней нагрузки, приложенной к контуру
– координаты главного вектора внешней нагрузки, приложенной к контуру  .
.
Таким образом, из однозначности напряжений и перемещений в многосвязной области  не следует однозначность всех искомых функций
не следует однозначность всех искомых функций 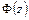 ,
, 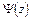 ,
,  ,
,  . Функции
. Функции 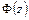 и
и 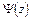 являются однозначными лишь в том случае, когда все главные векторы внешних нагрузок, приложенных к внутренним контурам области
являются однозначными лишь в том случае, когда все главные векторы внешних нагрузок, приложенных к внутренним контурам области  равны нулю.
равны нулю.
Заметим в заключение, что в соответствии с установленным в предыдущем параграфе фактом, напряжения в упругом теле не изменяются, если заменить функцию  на функцию
на функцию 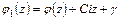 , а
, а  на
на 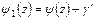 , где
, где 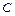 – действительная постоянная, а
– действительная постоянная, а 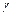 и
и 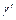 – комплексные. Чтобы остались неизменными при этом и перемещения в теле, постоянные
– комплексные. Чтобы остались неизменными при этом и перемещения в теле, постоянные 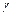 и
и 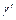 должны быть связаны соотношением
должны быть связаны соотношением  .
.
Дата добавления: 2015-07-10; просмотров: 86 | Нарушение авторских прав