
Читайте также:
|
Пусть  – область в плоскости комплексного переменного
– область в плоскости комплексного переменного  . Условимся граничные точки этой области обозначать буквой
. Условимся граничные точки этой области обозначать буквой 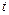 , а внутренние по-прежнему буквой
, а внутренние по-прежнему буквой  . Запись
. Запись  означает, что
означает, что 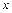 и
и 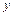 координаты рассматриваемой точки границы
координаты рассматриваемой точки границы  области
области  . Положение точки
. Положение точки 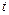 на каждом из контуров, составляющих
на каждом из контуров, составляющих  , однозначно определяется дуговой координатой
, однозначно определяется дуговой координатой  , которая отсчитывается в положительном направлении по данному контуру от некоторой фиксированной его точки. Поэтому любая функция
, которая отсчитывается в положительном направлении по данному контуру от некоторой фиксированной его точки. Поэтому любая функция 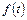 , заданная на
, заданная на  , на каждом из контуров представляет собой функцию действительной переменной
, на каждом из контуров представляет собой функцию действительной переменной  . Условимся сложную функцию
. Условимся сложную функцию  обозначать символом
обозначать символом  . Интегралы вида
. Интегралы вида
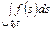 ,
,
взятые по некоторой дуге контура  , от точки
, от точки  до точки
до точки 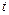 , будем обозначать так же через
, будем обозначать так же через
 .
.
Предположим вначале, что область  является конечной и односвязной. Ее граница состоит из одного замкнутого контура
является конечной и односвязной. Ее граница состоит из одного замкнутого контура  , который считаем гладким. Начало декартовой системы координат
, который считаем гладким. Начало декартовой системы координат  расположим во внутренней точке
расположим во внутренней точке  .
.
Во второй граничной задача плоской теории упругости на  заданы перемещения
заданы перемещения 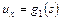 ,
,  . Функции
. Функции  и
и  по физическому смыслу задачи являются непрерывными функциями точки
по физическому смыслу задачи являются непрерывными функциями точки 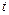 контура области
контура области  или соответствующей дуговой координаты
или соответствующей дуговой координаты  . Для внутренних точек области
. Для внутренних точек области 
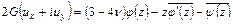 .
.
Поскольку перемещения  и
и  являются непрерывными функциями точек замкнутой области
являются непрерывными функциями точек замкнутой области 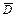 , то при
, то при 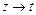 получим
получим
 на
на  . (9.1)
. (9.1)
Под левой частью этого равенства подразумевается предельное значение выражения  , когда
, когда  , оставаясь внутри области
, оставаясь внутри области  , стремится к точке
, стремится к точке 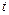 контура
контура  . Это граничное значение существует, так как функция
. Это граничное значение существует, так как функция 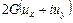 точек области
точек области 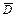 непрерывна.
непрерывна.
Во второй граничной задаче требуется найти аналитические функции  и
и  в
в 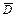 , если известно, что на границе
, если известно, что на границе  области
области  выполняется условие (9.1).
выполняется условие (9.1).
Рассмотрим теперь первую граничную задачу. По физическому смыслу напряжения в  являются непрерывными функциями. Будем рассматривать только те граничные задачи, в которых напряжения непрерывны в замкнутой области
являются непрерывными функциями. Будем рассматривать только те граничные задачи, в которых напряжения непрерывны в замкнутой области 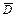 . Отсюда следует, что задаваемые напряжения необходимо непрерывны на границе области
. Отсюда следует, что задаваемые напряжения необходимо непрерывны на границе области  . В предположении, что граница области
. В предположении, что граница области  является гладкой и что напряжения и перемещения непрерывны в
является гладкой и что напряжения и перемещения непрерывны в 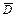 доказана единственность решения граничных задач плоской теории упругости [].
доказана единственность решения граничных задач плоской теории упругости [].
Для вывода граничного условия, которому должны удовлетворять искомые функции  и
и  , воспользуемся формулой (4.4), согласно которой
, воспользуемся формулой (4.4), согласно которой
 . (9.2)
. (9.2)
Здесь интегрирование производится вдоль произвольной гладкой дуги 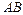 в
в  с начальной точкой
с начальной точкой  и конечной
и конечной  ,
,  и
и 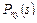 – координаты вектора напряжений
– координаты вектора напряжений  в точке дуги с дуговой координатой
в точке дуги с дуговой координатой  (начало отсчета дуг находится в точке
(начало отсчета дуг находится в точке  ).
).
В силу непрерывности напряжений в замкнутой области 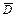 формула (9.2) оказывается справедливой и для дуги
формула (9.2) оказывается справедливой и для дуги 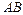 , принадлежащей границе области
, принадлежащей границе области  , то есть
, то есть
 , (9.3)
, (9.3)
где
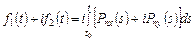 . (9.4)
. (9.4)
Выражение в левой части формулы (9.3) нужно принимать как граничное значение выражения  при стремлении
при стремлении  к точке
к точке 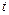 контура
контура  . Это граничное значение существует вследствие предположения о непрерывности напряжений в
. Это граничное значение существует вследствие предположения о непрерывности напряжений в 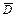
Таким образом, граничное условие, которому удовлетворяют искомые аналитические в  функции
функции  и
и  , в случае первой граничной задачи плоской теории упругости выражается формулой (9.2). при этом функции
, в случае первой граничной задачи плоской теории упругости выражается формулой (9.2). при этом функции  и
и  являются известными действительными функциями точек контура
являются известными действительными функциями точек контура  , определяемыми формулой (9.3) (положительное направление обхода контура
, определяемыми формулой (9.3) (положительное направление обхода контура  выбирается таким, чтобы область
выбирается таким, чтобы область  оставалась слева при движении вдоль
оставалась слева при движении вдоль  ).
).
Заметим, что постоянной, фигурирующей в правой части граничного условия (9.2), можно придать любое значение. Действительно, мы знаем, что напряженное состояние тела не изменится, если функции  и
и  заменить на
заменить на  и
и 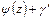 , где
, где 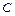 – действительная постоянная, а
– действительная постоянная, а 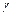 и
и 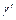 – комплексные постоянные. При этом
– комплексные постоянные. При этом  заменится на
заменится на 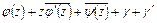 . Отсюда следует, что путем подходящего выбора одной из постоянных
. Отсюда следует, что путем подходящего выбора одной из постоянных 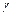 и
и 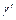 можно придать любое значение постоянной, фигурирующей в условии (9.2). Выбором оставшихся постоянных можно распорядится так, чтобы оказалось, например,
можно придать любое значение постоянной, фигурирующей в условии (9.2). Выбором оставшихся постоянных можно распорядится так, чтобы оказалось, например,
 или
или  и
и  . (9.5)
. (9.5)
Эти дополнительные условия вполне фиксируют искомые функции  и
и  при условии, что зафиксирована постоянная в правой части формулы (9.2).
при условии, что зафиксирована постоянная в правой части формулы (9.2).
В случае второй граничной задачи плоской теории упругости граничные условия (9.1) однозначно определяют перемещения всех точек упругого тела, а также напряжения. Но тогда по сказанному в § 5 надлежащим выбором констант 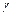 и
и 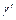 (напомним, что
(напомним, что  ,
,  ) можно добиться того, чтобы
) можно добиться того, чтобы
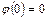 или
или 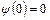 .
.
Эти дополнительные условия фиксируют искомые функции  и
и  при решении второй граничной задачи.
при решении второй граничной задачи.
Рассмотрим теперь случай бесконечной области  , ограниченной одним замкнутым гладким контуром
, ограниченной одним замкнутым гладким контуром  (бесконечная плоскость с отверстием). Граничные условия второй и первой задачи сохраняют прежний вид (см. (9.1) и (9.2)). В формуле (9.2) функция
(бесконечная плоскость с отверстием). Граничные условия второй и первой задачи сохраняют прежний вид (см. (9.1) и (9.2)). В формуле (9.2) функция  определяется формулой (9.3) при прежнем условии относительно выбора положительного направления обхода контура
определяется формулой (9.3) при прежнем условии относительно выбора положительного направления обхода контура  (область
(область  при обходе должна оставаться слева).
при обходе должна оставаться слева).
Искомые аналитические функции  и
и  в случае бесконечной области
в случае бесконечной области  не являются, вообще говоря, однозначными. На основании результатов § 7 в предположении, что начало координат находится внутри контура
не являются, вообще говоря, однозначными. На основании результатов § 7 в предположении, что начало координат находится внутри контура  , эти функции имеют структуру:
, эти функции имеют структуру:
 ,
,
 .
.
Здесь  ,
,  – однозначные в
– однозначные в  аналитические функции, включая бесконечно удаленную точку;
аналитические функции, включая бесконечно удаленную точку; 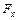 ,
, 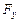 – координаты главного вектора внешних усилий, приложенных к границе
– координаты главного вектора внешних усилий, приложенных к границе  области
области  ;
; 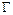 и
и  – комплексные постоянные, определяющие распределение напряжений на бесконечности и значение
– комплексные постоянные, определяющие распределение напряжений на бесконечности и значение
 .
.
Величины 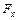 ,
, 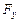 должны считаться заданными по условию во второй граничной задаче (в случае первой граничной задачи они могут быть вычислены по заданным на
должны считаться заданными по условию во второй граничной задаче (в случае первой граничной задачи они могут быть вычислены по заданным на  напряжениям). По условию считаются заданными во второй задаче постоянные
напряжениям). По условию считаются заданными во второй задаче постоянные 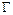 и
и  , а в случае первой задачи – постоянные
, а в случае первой задачи – постоянные 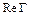 и
и  (мнимая часть постоянной
(мнимая часть постоянной 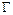 не влияет на распределение напряжений).
не влияет на распределение напряжений).
Рассмотрим в заключение случай многосвязной конечной области  , граница которой состоит из нескольких контуров:
, граница которой состоит из нескольких контуров:  ,
,  , …,
, …,  ,
,  . Искомые функции
. Искомые функции  ,
,  , вообще говоря, многозначны в
, вообще говоря, многозначны в  :
:
 ,
,
 .
.
Здесь 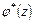 ,
,  – однозначные аналитические в
– однозначные аналитические в  функции,
функции, 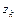 – произвольно взятые фиксированные точки внутри контуров
– произвольно взятые фиксированные точки внутри контуров  ,
,  ;
;  ,
,  – координаты главного вектора внешних нагрузок, приложенных к контуру
– координаты главного вектора внешних нагрузок, приложенных к контуру 
В случае первой граничной задачи величины  ,
,  известны (их можно вычислить по заданным внешним напряжениям на контурах границы области
известны (их можно вычислить по заданным внешним напряжениям на контурах границы области  ). В случае второй граничной задачи эти величины заранее не известны и подлежат определению вместе с функциями
). В случае второй граничной задачи эти величины заранее не известны и подлежат определению вместе с функциями 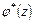 ,
,  .
.
Граничное условие второй задачи дается формулой (9.1), в которой под  нужно понимать совокупность контуров
нужно понимать совокупность контуров  ,
,  , …,
, …,  ,
,  границы области
границы области  . Граничное условие первой задачи на каждом из контуров
. Граничное условие первой задачи на каждом из контуров  можно записать так
можно записать так
 на
на  ,
,  ,
,
где  – некоторые постоянные, а
– некоторые постоянные, а
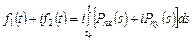 на
на  .
.
Здесь  – произвольно взятая фиксированная точка на
– произвольно взятая фиксированная точка на  . Положительное направление отсчета дуг на
. Положительное направление отсчета дуг на  считается то, которое оставляет область
считается то, которое оставляет область  слева.
слева.
Постоянные  не известны заранее. Одну из них, например
не известны заранее. Одну из них, например  , можно произвольно зафиксировать (выражение
, можно произвольно зафиксировать (выражение  определяется при заданных напряжениях с точностью до произвольного постоянного слагаемого). остальные постоянные
определяется при заданных напряжениях с точностью до произвольного постоянного слагаемого). остальные постоянные 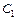 ,
,  , …,
, …,  являются неизвестными и подлежат определению вместе с функциями
являются неизвестными и подлежат определению вместе с функциями 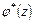 ,
,  .
.
Искомые функции 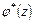 ,
,  могут быть зафиксированы при помощи дополнительных условий. Считая, что начало координат расположено в области
могут быть зафиксированы при помощи дополнительных условий. Считая, что начало координат расположено в области  , в случае второй граничной задачи можно положить
, в случае второй граничной задачи можно положить
 или
или  ,
,
А в случае первой задачи, считая постоянную  зафиксированной, можно считать
зафиксированной, можно считать
 или
или  ,
,  .
.
Если внимательно проследить за выводом граничных условий (9.1) и (9.2), то несложно заметить. Что для постановки граничных задач требуется непрерывность вплоть до границы  , то есть
, то есть  , выражений
, выражений
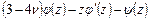 ,
,  (9.6)
(9.6)
Без обязательного требования непрерывности напряжений в  . Поэтому естественно заменить требование непрерывности напряжений
. Поэтому естественно заменить требование непрерывности напряжений 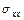 ,
, 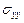 ,
, 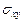 в
в  менее ограничительными требованиями непрерывности вплоть до границы
менее ограничительными требованиями непрерывности вплоть до границы  второго выражения (9.6). Однако в целях значительного упрощения рассуждений при изложении методов решения граничных задач плоской теории упругости наложим на искомые аналитические в
второго выражения (9.6). Однако в целях значительного упрощения рассуждений при изложении методов решения граничных задач плоской теории упругости наложим на искомые аналитические в  функции
функции  и
и  несколько более ограничительные условия: функции
несколько более ограничительные условия: функции  и
и  должны быть непрерывны в замкнутой области
должны быть непрерывны в замкнутой области  . Решение граничной задачи, обладающее этим свойством, будем называть регулярным.
. Решение граничной задачи, обладающее этим свойством, будем называть регулярным.
Если решение регулярно, то выражения (9.6) непрерывно продолжимы на  , так как функции
, так как функции  и
и  непрерывны в
непрерывны в  . Обратное же, вообще говоря, несправедливо.
. Обратное же, вообще говоря, несправедливо.
В дальнейшем, будем рассматривать лишь регулярные решения. В монографии [] доказаны теоремы единственности для первой и второй граничных задач в предположении, что рассматриваемые решения регулярны.
Дата добавления: 2015-07-10; просмотров: 62 | Нарушение авторских прав