Аппендикс 1

Приближение волновых фронтов

Рассмотрим некоторую комплексную амплитуду

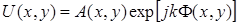(А 1.1)

свободно распространяющейся волны (рис. А 1.1), модуль амплитуды 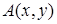которой меняются незначительно. Иными словами, волна промодулирована только по фазе . Естественно, что дальнейшее распространение такой волны приводит не только к искривлению волнового фронта, а и к изменению ее модуля амплитуды. Поэтому на некотором расстоянии от плоскости 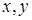в плоскости она уже промодулирована как по фазе, так и по интенсивности. Однако, если фазовая модуляция подчиняется определенным ограничениям, то процесс распространения волны от плоскости к плоскости осуществляется практически без дифракции. Алгоритмизацию такого процесса можно провести, применяя соответствующие методы аппроксимации, например метод стационарной фазы [28; 94].

Поле в плоскости связано с полем в плоскости 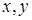преобразованием Френеля

. (А 1.2)

В соответствии с методом стационарной фазы, если модуль амплитуды волны 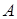, заданный в , – функция с острым спектром а фаза F изменяется достаточно плавно, выражение (А 1.2) может быть существенно упрощено.

Двумерная интерпретация метода стационарной фазы имеет вид:

~ , (А 1.3)

где – дважды дифференцируемая в функция; принадлежат к области и являются решением системы уравнений:

. (А1.4)

Причем точка одна единственная такая точка в ; – частные производные в точке соответственно, а для вторых производных выполняются условия:

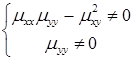. (А 1.5)

В нашем случае

= . (А 1.6)

Из (А 1.6) вытекает, что должна быть дважды дифференцируемой функцией в . Система (А 1.4) трансформируется к следующему виду:

, (А 1.7)

а условия (А 1.5) к

, (А 1.8)

где – 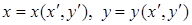решения системы уравнений (А1.7). Тогда поле в плоскости можно описать выражением

. (А 1.9)

В случае, когда такая точка не единственная в области , поле определяется как сумма полей типа (А 1.9), соответствующих каждому решению. Если же решений системы (А 1.7) бесконечно много, т.е. хотя бы одно из решений этой системы вырождается в неопределенность, то поле, соответствующее этой неопределенности, вырождается в d- функцию. Физически такая ситуация соответствует формированию каустики, или точке фокусировки сферической волны.

Выражение (А 1.9) будем называть «приближением волновых фронтов».

Одномерная интерпретация приближения волновых фронтов имеет вид

, (А 1.10)

где – первая и вторая производные от фазовой модуляции; – решение уравнения

. (А 1.11)

При этом выполняется условие

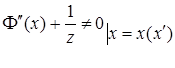. (А1.12)

Проанализируем требования к волне, при выполнении которых ее распространение может быть описано с помощью такого приближения.

Для простоты рассмотрим одномерный случай. Разложим 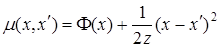по степенями 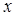в окрестности x ₀ решения уравнения (А 1.11). Тогда выражение (А 1.2), с учетом того факта, что , принимает вид:

. (А 1.13)

Фактически, интеграл в (А 1.13) может быть интерпретирован как некоторое поле, сформированное транспарантом с пропусканием , который освещается плоской волной на расстоянии от плоскости . Для того, чтобы поле в плоскости описывалось соотношением (А 1.10), т.е. было пропорционально , необходимо, чтобы для соотношения (А 1.13) выполнялось приближение, аналогичное приближению «тени» [94].

Сделаем замену

. (А 1.14)

Соответственно комплексная амплитуда может быть описана выражением

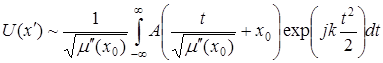. (А 1.15)

Введем для угловой спектр

. (А 1.16)

В результате, можно показать, что:

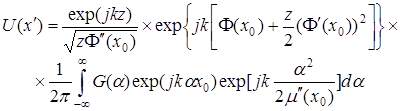. (А1.17)

Очевидно, если мало отличается от единицы для некоторой окрестности (), а – функция с широким спектром (т.е. быстро уменьшается для не принадлежащих окрестности), то (А 1.17) трансформируется в (А 1.10). Другими словами, , если ®1, где – некоторая предельная пространственная частота, начиная с которой вкладом компонент углового спектра в результирующее поле можно пренебречь.

Известно, что для прямоугольного отверстия такая предельная частота часто определяется как (2 a – размеры отверстия) и отвечает первому минимуму углового спектра. Кроме того, известно, что в нулевом максимуме спектра сосредоточено более чем 90% энергии излучения, пропускаемой отверстием. По аналогии с отверстием, под предельными частотами будем понимать полосу частот, в границах которой переносится более чем 90% энергии, ассоциируемой с . Таким образом, удовлетворяет условию

. (А 1.18)

В соответствии с критерием Релея, , если .

Таким образом, условие (А 1.18) и соотношение:

(А 1.19)

формируют критерий применимости приближения волновых фронтов.

Дата добавления: 2015-07-12