Сети вихрей – скелетон фазы скалярного поля 6 страница

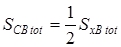. (3.50)

Можно показать, что при интегрировании по контуру, охватывающему область A,соотношение (3.48 a) преобразуется к виду:

. (3.51)

Из (3.50) и (3.51) следует, что:

. (3.52)

Выражение (3.52) справедливо и в случае, когда областей типа B внутри области A не одна.

Таким образом, суммарный топологический индекс -точек в области A определяется суммарным топологическим зарядом всех вихрей, лежащих на -контурах, ограничивающих эту область. Добавим, что это утверждение остается справедливым, если внутренние области в свою очередь содержат области с другим типом поляризации.

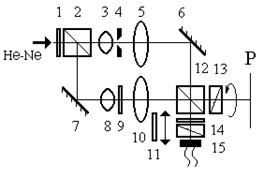
Экспериментальные исследования [81] в подтверждение проведенного рассмотрения проводились в расположении (подобном к расположению, представленному на рис. 3.9), иллюстрируемом рисунком 3.19. В интерферометр Маха – Цандера, образованный светоделителями 2,12 и зеркалами 7,6, направлялся линейно поляризованный лазерный пучок. Пластинка (1) преобразует линейно поляризованное излучение в циркулярно поляризованное. В объектном канале пучок фокусировался микрообъективом 8 и направлялся на рассеивающий объект – тонкую полимерную пластинку 9. Объект был подобран таким образом, что рассеянное им поле было «интегрально деполяризовано» со степенью деполяризации не более 50%. Степень поляризации как интегральная характеристика всего исследуемого участка поля подсчитывалась на основании анализа усредненных параметров Стокса в соответствии с известным соотношением [28]:

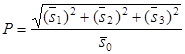. (3.53)

Как будет показано в п. 3.5 в случае освещения такого объекта циркулярно поляризованным пучком, -контуры невелики по размерам и включают, как правило, области с одним типом поляризации (правая или левая). Иными словами, такие области не содержат вложенных -контуров. Анализ поля в дальней зоне обеспечивается тем, что рассеивающий объект располагается в фокальной плоскости объектива 10.

Тогда практически сразу за объективом анализируемое поле подчиняется условию дальней зоны. Опорный пучок формируется коллиматором 3 – 5. На выходе интерферометра устанавливается анализатор 13, позволяющий выделять любую поляризационную проекцию выходного поля и визуально анализировать результат интерференции поля рассеянного объектом и плоским опорным пучком. Такое оптическое расположение, как было показано выше (см. п. 3.2.3), позволяет провести полный интерференционный анализ поляризационных сингулярностей по интерферограммам поляризационных проекций векторного поля. Для реконструкции -контура и определения положения вихрей ортогональных линейно поляризационных компонент поворотом анализатора 13 выбирались соответствующие проекции векторного поля. Угловой шаг поворота анализатора составлял 20°. Для определения положения С -точек в схему непосредственно за объективом 10 вводилась пластинка (11) с известной ориентацией ее оси относительно оси анализатора для получения поляризационных проекций, соответствующих лево- и правоциркулярно поляризованным компонентам поля. Положение вихрей таких ортогонально поляризованных компонент совпадает с позицией -точек. Координаты вихрей ортогональных компонент (линейно- или циркулярно поляризованных) определяются исходя из позицией интерференционных вилочек, наблюдаемых в интерферограммах, соответствующих поляризационных проекций. С другой стороны светоделителя 12 на выходе интерферометра расположен стокс-поляриметр 13, 14 и фотоприемник 15, позволяющие (при закрытом опорном пучке) осуществить измерения усредненных поляризационных характеристик поля, в том числе и степени поляризации, как интегральной характеристики анализируемого поля.

На рис. 3.20 представлены результаты экспериментальных исследований поля, рассеянного объектом. В левой колонке приведены некоторые из интерферограмм линейно поляризованных проекций поля объекта. Ориентация главной оси анализатора 13 соответствует углам 80°, 100°, 160°. Рисунки в правой колонке иллюстрируют положение восстановленных -контуров и -точек.

На -контурах обозначены соответствующие данной поляризационной проекции вихри. Их топологические заряды обозначены кружками со знаками (+) или (–). Топологическим зарядам вихрей +1 соответствуют интерференционные вилочки, направленные вниз; отрицательным вихрям – вилочки, направленные вверх. -точки на рисунке обозначены серыми квадратами и ромбами с соответствующим знаком внутри. Из рисунков видно, что -контуру с одним вихрем (топологический заряд вихря +1) (самый верхний -контур) принадлежит одна -точка с топологическим индексом +1/2. Внутри нижнего (самого большого) -контура с двумя вихрями разного знака (нулевой суммарный топологический заряд) находятся две -точки с индексами +1/2 и –1/2. Таким образом, суммарный топологический индекс -точек, расположенных внутри контура, равен нулю. Внутри левого -контура -точки отсутствуют. Соответственно сумма топологических зарядов вихрей линейно поляризованной компоненты равна нулю.

Интересно отметить, что некоторые поляризационные проекции не содержат вихрей, расположенных на -контуре, если такой контур окружает область, в которой суммарный топологический индекс -точек равен нулю. Такой ситуации соответствует поляризационная проекция, представленная на рисунке (а). Для левого контура вместо двух вихрей наблюдается точка их аннигиляции (рождения).

Рис. 3.20

Характеристики С-точек и вихри линейно поляризованных компонент.

Степень интегральной деполяризации рассеянного поля 46%

Левая колонка – поляризационные проекции, соответствующие ориентации главной оси анализатора 80°, 100°, 160° (рисунки a, b, c соответственно). Правая колонка – положение s-контуров, C -точек и вихрей линейно поляризованных проекций векторного поля. – вихри линейно поляризованных ортогональных компонент, – точка их аннигиляции (рождения), – левополяризованные C- точки, – правополяризованные C- точки. Знаки 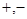соответствуют позитивным, негативным топологическим зарядам вихрей и топологическим индексам C -точек.

3.6. Элементарные поляризационные структуры и элементарные поляризационные сингулярности векторных полей

Естественно, что для векторного поля общего вида анализ топологических особенностей и поиски взаимосвязи между поведением поляризационных параметров поля и характеристиками его топологической структуры является непростой задачей. Поэтому, на наш взгляд, было бы полезно предварительно рассмотреть некоторые элементарные поляризационные структуры, связанные с -контурами и -точками, а затем на основе полученных фактов перейти к анализу полей более общего вида.

Элементарные поляризационные ситуации, возникающие в векторном поле были, всесторонне рассмотрены [77] в областях, которые непосредственно прилегают к поляризационным сингулярностям. Однако этот анализ носил локальный характер и включал только один тип поляризационных сингулярностей. В то же время, как следует из п. 3.1, все типы векторных сингулярностей жестко взаимосвязаны.

Именно поэтому целесообразно рассмотреть поля с относительно простой поляризационной структурой, которые содержат оба типа поляризационных сингулярностей: -контур и -точку.

Очевидно, что такие элементарные векторные поля могут образовываться в результате суперпозиции соответствующих однородно поляризованных простых полей, структуру которых можно предположить из разложения векторного поля с требуемыми характеристиками поляризационных сингулярностей на ортогональные компоненты.

Исходя из этого, элементарные поляризационные сингулярности можно синтезировать двумя путями:

· в результате интерференции двух ортогональных линейно поляризованных вихревых пучков [82; 83];

· как следствие суперпозиции двух ортогонально поляризованных циркулярно поляризованных относительно простых пучков [107].

3.6.1. поляризационные структуры, полученные в результате интерференции линейно поляризованных пучков

Естественно, что наиболее «простые» векторные поля содержат
-контуры с минимальным количеством вихрей (два) разности фаз. Иными словами, любая поляризационная проекция векторного поля должна содержать один вихрь. Чтобы область, ограниченная -контуром, имела отличный от нуля суммарный топологический индекс () эти вихри должны принадлежать к разным ортогональным компонентам [82], т.е. суммарное поле можно рассматривать как суперпозицию двух ортогонально поляризованных вихревых пучков.

Допустим для простоты, что оба вихревых пучка – изотропные вихри (см. [12] и п. 1.1). В полярной системе координат с началом в центре вихря комплексная амплитуда такого пучка описывается соотношением

, (3.54)

где 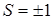– топологический заряд; – начальная фаза вихревого пучка; 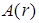– модуль амплитуды, в центре вихря равный нулю.

Пусть вихревые пучки распространяются параллельно друг другу и центры вихрей находятся на расстоянии 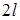. Введем Декартову систему координат () таким образом, чтобы ее начало было на одинаковом расстоянии от центров обоих вихрей, ось проходила через центры обоих вихрей, а направление оси 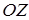совпадало бы с направлением распространения пучков.

Легко показать, что контур, отвечающий произвольной разности фаз , определенный с точностью до , описывается соотношением:

, (3.55)

где ; – разность начальных фаз вихревых пучков; – их топологические заряды.

Есл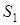и и одного знака, то (3.55) трансформируется к виду:

. (3.56)

Есл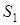и и разных знаков, то (3.55) переходит в соотношение:

. (3.57)

Уравнение (3.57) определяет контуры гиперболического типа, т.е. незамкнутые. Поэтому более подробно проанализируем только соотношение (3.56). Соотношение (3.56) – уравнение окружности, радиус и положение центра которой определяются расстоянием между вихрями и соотношением разности фаз . Заметим, что в случае формирования суммарного поля анизотропными вихрями, (3.56) трансформируется в уравнение эллипса. Аналогичными соотношениями описываются контуры суммарного поля, возникающего в результате суперпозиции вихрей с любой структурой, если расстояние между ними меньше, чем размеры зоны ядра вихря.

Обратимся вновь к соотношению (3.56). Пусть поперечные размеры вихревых пучков значительно превышают расстояние между их центрами и , где 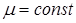. Тогда можно утверждать, что для любой точки поля, за исключением области поля, непосредственно прилегающей к центрам вихрей, где и достигают нулевого значения, выполняется соотношение:

. (3.58)

Связь между отношением модулей амплитуд компонент, разностью фаз и размерами полуосей эллипсов определяется выражением [28]:

, (3.59)

где ; – малая и большая полуоси поляризационного эллипса соответственно; .

Из (3.59) следует, что отличие поляризационных характеристик, определяемое разностью эксцентриситетов эллипсов в разных точках поля, практически определяется отличием 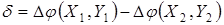в разности фаз, соответствующих точкам поля 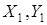и . Будем считать, что поляризационные характеристики поля в этих точках отличаются мало, если , что отвечает изменению на величину порядка 0,2. Из (3.56) следует, что область, в которой наблюдаются существенные различия поляризационных характеристик поля, прилегает непосредственно к центрам вихрей и ограничена контурами разности фаз, для которых 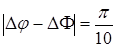. Уравнение таких контуров описывается выражением

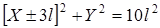(3.60)

независимо от разности фаз 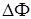в вихревых пучках, т.е. определяется только расстоянием между центрами вихрей. Причем контур разности фаз, отвечающий с точностью до , – прямая, проходящая через центры обоих вихрей (рис. 3.21).

При 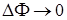-контур – окружность с диаметром, равным расстоянию между вихрями (рис. 3.21 a). Обе -точки находятся на одинаковом расстоянии от вихрей. При (рис. 3.21с) одна из -точек стремится занять положение на прямой, соединяющей вихри, а вторая расположена на бесконечности. Рис. 3.21 b отвечает .

На рис. 3.22 – 3.25 приведены результаты компьютерного моделирования элементарных поляризационных сингулярностей, возникших вследствие интерференции ортогонально поляризованных вихревых пучков. При этом менялась не только разность фаз между вихревыми пучками, а и параметры самих вихрей, такие как знак топологического заряда, кривизна эквифазных линий в непосредственной близости от центра вихря. Рисунки

Рис. 3.22.

Интерференция изотропных вихрей одного знака с разностью фаз между вихревыми пучками . a,b – фазовые карты вихрей, с – поведение разности фаз результирующего пучка

a b c

Рис. 3.23

Интерференция изотропных вихрей одного знака и небольшой разницей в величине кривизны эквифазных линий в зоне ядра вихрей.

a b c

Рис. 3.24

Интерференция изотропных вихрей одного знака со значительной разницей в величине кривизны эквифазных линий в зоне ядра вихрей.

a b c

Рис. 3.25

Интерференция изотропных вихрей разных знаков

a, b – фазовые карты интерферирующих вихрей. Рисунки с – разность фаз
результирующего поля, приведенная с точностью до (разности фаз, отличающиеся на , обозначены одинаковыми оттенками серого). Положение - и - контуров указано стрелками.

Рис. 3.22 соответствует интерференции изотропных вихрей с общей разностью фаз между вихревыми пучками . Как следует из проведенного рассмотрения, все контуры разности фаз – окружности. Рисунок 3.23 иллюстрирует тот факт, что пока расстояние между центрами вихревых пучков такое, что эквифазные линии в зоне ядра не слишком изогнуты, контур разности фаз, соответствующий с точностью до модуля общей разности фаз между вихревыми пучками (в данном случае ), замкнутый, а его размеры сравнимы с расстоянием между центрами вихрей. Естественно, что форма контура при этом искажается. При дальнейшем увеличении кривизны эквифазных линий поля фазы интерферирующих вихрей (или увеличения расстояния между ними) такие контуры разрываются и трансформируются в контуры сложной формы, например, в контуры в виде спиралей (см. рис. 3.24). Для сравнения на рис. 3.25 представлены результаты моделирования интерференции вихрей, знаки топологических зарядов которых различны. Как видно из рисунка, даже для изотропных вихрей все контуры разности фаз незамкнуты.

Дополнительно остановимся на рисунке 3.23. Как видно внутренний -контур, проходящий через центры вихревых пучков, окружен группой дополнительных -контуров. Иными словами образовалась структура вложенных -контуров типа «матрешки». Причем в базисе разложения, отвечающем рисунку на внешних контурах вихрей разности фаз нет. Из этого факта следует вывод, что изменение азимута линейной поляризации при обходе любого внешнего контура не достигает . Как следствие – суммарный топологический заряд -точек в середине каждого внешнего -контура равняется нулю.

3.6.2. Элементарные поляризационные сингулярности, полученные в результате интерференции циркулярно поляризованных пучков

Напомним, что -точку векторного поля можно ассоциировать с вихрем одной из циркулярно поляризованных ортогональных компонент векторного поля. Очевидно, что элементарные поляризационные структуры будут образовываться при условии, что в точке циркулярной поляризации одна из компонент нулевая. Как следствие – поляризационная ячейка, содержащая -сингулярность, может быть синтезирована в результате суперпозиции циркулярно поляризованных вихревого и гладкого пучков.

Комплексные амплитуды линейно поляризованных компонент в терминах право- и левоциркулярно поляризованных составляющих описываются системой

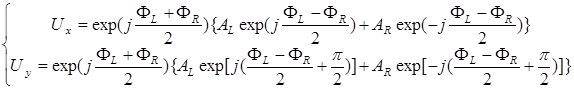.(3.61)

В терминах главной фазы и азимута поляризации (3.61) приобретают вид

. (3.62)

Представим себе, что в процессе суперпозиции пучков возникает дополнительная разность фаз между интерферирующими пучками . Естественно, что локализация и характеристики -точки (топологический заряд, индекс) при таком изменении условий суперпозиции не изменится. Этот факт следует из анализа (3.61) и (3.62). Вместе с тем, из этих же соотношений вытекает, что азимут поляризации и главная фаза изменяются на величину, соответствующую во всех точках поля.

Для точек поля вдоль -контура, для которых соотношения (3.61) и (3.62)трансформируются

, (3.63)

и

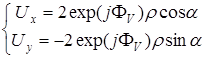. (3.64)

Из этих соотношений следует, что при изменении общей разности фаз между пучками локализация -контуров не изменится, а вектор поля в каждой точке контура повернется на угол . Направление изменения азимута (+ или – ) зависит от знака дополнительной разности фаз и от того, в какой пучок (право- или левополяризованный) она вносится. Из этих же соотношений следует, что при изменении разности фаз на 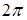изменение азимута равно , т.е. ориентация векторов поля вдоль -контура такая же, как и при .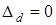

Таким образом, разница между способами формирования элементарных поляризационных структур заключается в следующем. Если изменяется разность фаз между интерферирующими линейно поляризованными вихревыми пучками, изменяется форма -контуров и локализация -точек. В то же время при формировании элементарных поляризационных структур с помощью суперпозиции циркулярно поляризованных пучков изменение фаз между ними приводит к вращению вектора линейной поляризации вдоль -контура и соответствующему вращению поляризационных эллипсов внутри области, ограниченной этим контуром. Позиции и характеристики -точек при этом остаются неизменными.

3.6.3. Экспериментальное моделирование элементарных поляризационных сингулярностей

Физическое моделирование элементарных поляризационных областей, которые образуются в результате интерференции линейно поляризованных пучков было проведено в экспериментальном расположении, приведенном на рисунке 3.26 [82; 83]. Линейно поляризованный лазерный пучок направляется в «двойной» интерферометр типа Маха – Цандера. Перед светоделитем 2 устанавливается фазовращающая пластинка , преобразующая линейную поляризацию в циркулярную. В одном из каналов интерферометра устанавливается синтезированная голограмма 3, полученная по методике, описанной в [37 – 39]. В результате дифракции на такой голограмме Гауссовый пучок преобразуется в вихревой c единичным топологическим зарядом. После расширения и фильтрации пучка коллиматором 4, 5, 6 образуется циркулярно поляризованный вихрь, близкий к изотропному. Далее вихревой пучок направляется во внутренний интерферометр. В плечах интерферометра размещаются скрещенные поляризаторы 8, 12, т.е формируются ортогонально поляризованные вихревые пучки. Одно из зеркал интерферометра 9 устанавливается на пьезокерамику, которая дает возможность варьировать разность фаз между пучками в пределах 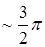. С помощью светоделителя 10 зеркал 9, 11 изменяется расстояние между центрами вихревых пучков и задается одинаковое направление распространения пучков. С помощью делителя 17 результирующее поле смешивается с опорным пучком и в плоскости 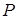наблюдается интерференционная картина. Для визуализации движения вихрей вдоль -контура после делителя 17 устанавливается анализатор 18. Для фиксации положения интерференционной вилочки в плоскости наблюдения формируется репер в виде дифракционной картины от прямоугольного отверстия.

Дата добавления: 2015-07-12