Сети вихрей – скелетон фазы скалярного поля 9 страница

Более того, оптическая сингулярность может быть обнаружена лишь «косвенными» непрямыми методами интерферометрии в результате анализа поля, образованного сингулярной структурой и некоторым «опорным» полем [8 – 10; 36 – 39; 84; 85].

Исходя из таких соображений, следует, казалось бы, очевидный, логический вывод – единственным резоном рассмотрения оптических сингулярностей является их «роль в формировании структуры» оптического поля – как скалярного, так и векторного.

С другой стороны, наличие сингулярности любого из параметров поля неминуемо должно приводить к неким физическим особенностям поля, образованного в ее окрестности.

Возникает вопрос, в чем же состоит физическое проявление оптических сингулярностей? Проявление, характеризующееся специфическим поведением физической системы, на которую воздействует электромагнитная волна.

Для скалярных вихрей такое проявление, как известно, связано с тем, что в области оптического вихря возникает орбитальный момент импульса электромагнитного поля [100 – 104]. Такой момент появляется благодаря специфической (геликоидальной) фазовой поверхности в окрестности вихря, т.е., вообще говоря, специфического поведения поля во времени. Иными словами, физическое проявление скалярной сингулярности отображается в специфическом временном поведении компонент электромагнитного поля.

Поляризационные сингулярности, в конечном итоге, тоже должны рассматриваться как временные особенности поля, поскольку характеристики волны, содержащие сингулярности: поляризационный азимут, вибрационная фаза, направление вращения вектора поля определяют поведение вектора поля – как в пространстве, так и во времени. Очевидно, что и для случая векторных сингулярностей, их физическое проявление должно быть тоже связано с временным поведением поля, которое в конечном итоге сводится к специфической величине момента импульса электромагнитного поля в области сингулярности, поведению этой характеристики поля отличному от поведения в других областях поля.

Как известно (см., например, [101]) «прямое силовое» (или «энергетическое») воздействие электромагнитной волны на некоторую физическую систему ассоциируется с вектором Умова – Пойнтинга. Во всяком случае, пространственное распределение параметров этого вектора (величины и ориентации) является одним из основных факторов, определяющих воздействие волны на систему. Кроме того, вектор Умова – Пойнтинга непосредственно связан с моментом импульса (см., например, [100; 101]). Однако, в отличие от момента импульса, вектор Умова – Пойнтинга не «привязан» к точке приложения (оси момента). В то же время, информация о поведении этого вектора позволяет легко перейти к анализу самого момента импульса поля в произвольной области.

Естественно, что для поля общего типа характеристики компонент вектора Умова – Пойнтинга (в том числе и поперечной: модуль и ориентация) могут рассматриваться как некоторые пространственно распределенные параметры поля. В общем случае такие распределения имеют особенности, включая сингулярности. Как и традиционные оптические сингулярности, сингулярности вектора Умова – Пойнтинга можно объединять в сети, которые должны (хотя бы на качественном уровне) определять поведение вектора Умова – Пойнтинга в любой точке, формировать скелетон поля этого вектора, т.е. задавать закономерности формирования пространственных распределений его параметров.

Очевидно (как это уже наблюдалось для фазы и интенсивности, поляризации и интенсивности (см. п.2.6 и п.3.3)), что характеристики таких сингулярных множеств, поведение вектора Умова – Пойнтинга должны быть связаны с характеристиками сетей традиционных сингулярностей.

Исходя из этого, анализ сингулярностей вектора Умова – Пойнтинга, установление соответствующих топологических закономерностей является актуальной задачей. Добавим, что прикладные аспекты такого рассмотрения непосредственно связаны с областью научных исследований, которая интенсивно развивается, с так называемыми оптическими пинцетами (см., например, [104]).

4.1. Общие допущения. Компоненты вектора Умова – Пойнтинга

Как и раньше, рассмотрение будем проводить при условии выполнения параксиального приближения. Однако, в отличие от традиционного подхода [100], будем анализировать не только усредненный по времени, но и мгновенный вектор Умова – Пойнтинга.

Резоны такого рассмотрения следующие:

1. Операция усреднения полностью имеет смысл только для оптической волны, что обусловлено слишком быстрыми изменениями поля во времени. Что же касается радиоволн, то их период колебания, может быть, сравним со временем реакции физической системы. В этом случае энергетическое воздействие волны на такую систему определяется поведением неусредненного вектора Умова – Пойнтинга или, по крайней мере, усредненного по гораздо меньшему интервалу времени .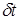

Аналогично концепция наевской дисклинации является фундаментальным понятием для радиоволн и теряет свою силу в оптике [82; 83].

2. Заметим также, что рассмотрение поведения компонент во времени дает нам дополнительную информацию для более детального понимания процессов формирования усредненного вектора Умова – Пойнтинга.

Можно показать, что в случае выполнения параксиального приближения (см. Аппендикс 3) для компонент вектора Умова – Пойнтинга выполняются следующие соотношения:

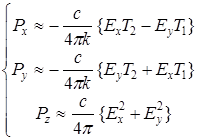, (4.1)

где

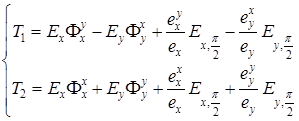, (4.2)

и

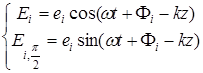, (4.3)

где 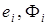– модули амплитуд и фазы компонент соответственно; 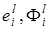– их производные; .

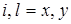Как следует из этих соотношений, при выполнении параксиального приближения, компоненты вектора Умова – Пойнтинга могут быть записаны как функции, определяемые только -, -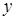компонентами электрического поля.

Именно эти соотношения и их версии и будут базовыми при нашем анализе.

4.2. Сингулярности вектора Умова – Пойнтинга в скалярных полях

Сначала уточним понятие скалярного поля в соответствии с условиями нашего анализа.

Как правило, поле, поляризованное однородно можно, рассматривать как скалярное, независимо от типа поляризации [8]. В нашем случае придется сузить понятие скалярного поля до линейно поляризованного, поскольку для эллиптически поляризованного поля поведение вектора Умова – Пойнтинга может быть достаточно сложным и нетривиальным. В частности у эллиптически поляризованной волны может возникать так называемый спиновый момент импульса [100].

4.2.1. Мгновенные сингулярности скалярного поля

Достаточно просто показать, что для волны, линейно поляризованной вдоль оси 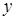(выбор оси не является принципиальным), «скалярная версия» базовых уравнений имеет вид:

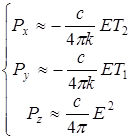, (4.4) 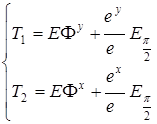, (4.5) . (4.6)

Как следует из этих соотношений, сингулярности вектора Умова – Пойнтинга могут возникать в двух случаях:

1. Все три компоненты равняются нулю в определенный момент времени. Этот случай соответствует возникновению дисклинации.

2. Только поперечная компонента равна нулю. Эта ситуация соответствует одновременному равенству нулю величин 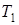и .

Исходя из этого, возникновение дефекта вектора Умова – Пойнтинга при одновременном равенстве нулю всех трех компонент требует уточнения понятия дисклинации для скалярного поля.

Можно показать, что в отличие от векторного поля, в котором дисклинации – линии, движущиеся в трехмерном пространстве, или соответствующие точки в сечении поля, дисклинации в скалярном поле вырождаются в нулевые поверхности или в соответствующие замкнутые лини в сечении поля. Другими словами, в отличие от векторного поля, где дисклинации – «точечные» дефекты, в скалярном поле они движущиеся «краевые» дефекты. Более того, точечные дисклинаци не существуют в скалярном поле. Отсутствие точечных дисклинаций можно объяснить, исходя из непрерывности поля и того факта, что амплитуда линейно поляризованной волны в каждой точке поля дважды за период колебания принимает нулевое значение.

Такое поведение поля иллюстрируется поведением поперечной компоненты вектора Умова – Пойнтинга в области изотропного вихря (рис. 4.2).

a b c d

Рис. 4.2

Вращение краевой дисклинации в области изотропного вихря.

a – распределение интенсивности изотропного вихря; b – d – мгновенное распределение модуля поперечной компоненты вектора Умова – Пойнтинга для разных моментов времени, определяющих положение дисклинации.

Можно показать, что поперечная компонента вращается вокруг центра вихря с двойной частотой колебания волны. Направление вращения определяется знаком топологического заряда вихря.

Мгновенная ориентация компоненты вектора Умова – Пойнтинга для разных моментов времени (рис. 4.3) описывается таким соотношением:

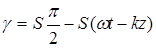, (4.7)

где – топологический заряд вихря.

a b c

Рис. 4.3.

Мгновенная ориентация поперечной компоненты вектора Умова – Пойнтинга для различных моментов времени.

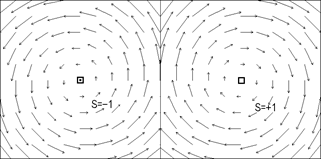Как следует из (4.7) и рисунка 4.3, азимут вектора Умова – Пойнтинга для определенного момента времени не зависит от 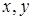и меняется скачком при переходе через дисклинацию.

Таким образом, хорошо известная прецессия (см., например, [100]) усредненного вектора Умова – Пойнтинга около центра вихря (рис. 4.4) является результатом усреднения одинаково ориентированных векторов.

Из рисунка следует, что азимут усредненной компоненты вектора Умова – Пойнтинга имеет сингулярность в центре вихря. Это сингулярность типа «центр» [88]. Оба случая, и (a) и (b), ассоциируются с позитивным индексом Пуанкаре 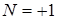. Поэтому для полной характеристики такой сингулярности вектора Умова – Пойнтинга необходимо ввести дополнительный параметр типа хиральности 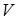. Пусть положительная хиральность 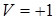(рис. 4.4 b) соответствует прецессии вектора по часовой стрелке и отрицательная 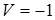(рис. 4.4 a) характеризует противоположно направленную прецессию. В дальнейшем будем называть такие

a b c d

Рис. 4.5

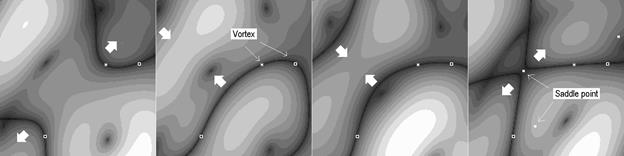
Временное поведение модуля поперечной компоненты случайного скалярного поля.

Направление движения дисклинаций указано на рисунках белыми стрелками.

сингулярности азимута вектора Умова – Пойнтинга и подобные им „ вихревыми ” сингулярностями.

Ситуация значительно сложнее для скалярного поля общего вида, однако поведение вектора Умова – Пойнтинга подобно случаю изотропного вихря. Временное поведение поперечной компоненты для участка случайного скалярного поля иллюстрируется рисунком 4.5. Краевые дисклинации вращаются около центров вихрей поля в соответствии со знаками их топологических зарядов. Дисклинации, вращающиеся в разных направлениях, соответствующие соседним вихрям, сходятся в седловых точках фазы (рис. 4.5 b; c; d) и снова расходятся в направлении ортогональном к направлению их сближения (рис. 4.5 a). Направление движения дисклинаций указано на рисунках белыми стрелками.

Второй тип мгновенных дефектов, возникающий в скалярном поле, – это дефекты поперечной составляющей вектора Пойнтинга, соответствующие ее нулевому значению и ненулевому значению -компоненты. Такие сингулярности имеют точечный характер. Возможные реализации точечных сиснгулярностей могут быть сведены к типам структур, представленных на рис. 4.6.

Характерное поведение поперечной составляющей вектора Умова – Пойнтинга в областях, соответствующих всем типам точечных сингулярностей, полученных в результате компьютерного моделирования, иллюстрируется рис. 4.7.

Очевидно, что в отличие от вихревых сингулярностей, усредненный по пространственным координатам и малому отрезку времени 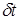момент импульса поля равен нулю в небольшой окрестности такой сингулярности. Поэтому в дальнейшем будем называть такого типа сингулярности «пассивными».

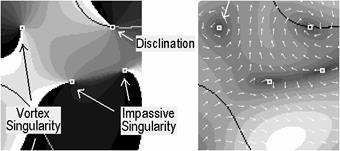
Из рисунков 4.6, 4.7 видно, что пассивные сингулярности могут характеризоваться как положительным (сингулярность типа «звезда» – рис. 4.6 b, c и рис. 4.7 a, c), так и отрицательным (сингулярность типа «седло» – 4.6 a и рис. 4.7 b) индексом Пуанкаре.

Соседние пассивные сингулярности разных знаков объединяются линиями тока поперечной составляющей вектора Умова – Пойнтинга в сингулярные сети. Причем седловой характер отрицательной сингулярности обеспечивает топологическую связь между положительными дефектами. Поэтому такие сингулярности рождаются и исчезают парами ((+) и (–) сингулярность) без образования дополнительных дефектов.

Движение таких сингулярностей подчиняется определенным закономерностям. В частности, анализ (4.4) – (4.6) приводит к выводу, что точечные пассивные сингулярности обязательно проходят через все стационарные точки фазы и интенсивности.

4.2.2. Усредненные сингулярности вектора Умова – Пойнтинга скалярного поля

Легко можно показать, что усредненная версия соотношений (4.6) имеет вид:

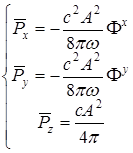, (4.8)

где 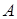– модуль амплитуды; 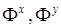– производные от фазы.

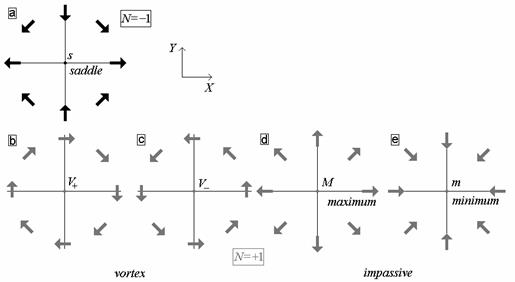
Рис. 4.8

Возможное поведение вектора Умова – Пойнтинга в окрестности

усредненных сингулярностей скалярного поля.

b, c – вихревые сингулярности; a, d, e – пассивные сингулярности поперечной компоненты вектора Умова – Пойнтинга.

Как и в случае мгновенного вектора Умова – Пойнтинга существует возможность возникновения двух типов сингулярностей:

1. Все компоненты усредненного вектора Умова – Пойнтинга равны нулю (рис. 4.8 b, c). Этот случай соответствует усредненной вихревой сингулярности, локализованной в центре вихря. Модуль амплитуды нулевой. В области центра вихря наблюдается «классическая» прецессия вектора Умова – Пойнтинга. Такая сингулярность азимута вектора Умова – Пойнтинга характеризуется положительным индексом Пуанкаре. Вихрям, различающимся знаком топологического заряда, соответствуют сингулярности с различной хиральностью.

2. Только поперечная компонента исчезает (рис. 4.8 a, d, e). Это усредненные пассивные сингулярности. Как следует из системы (4.8), их координаты совпадают с координатами стационарных точек фазы поля. Направление распространения энергии в этих точках совпадает с осью .

Другими словами, именно эти точки поля «задают» преимущественное направление распространения скалярной волны.

Возможное поведение вектора Умова – Пойнтинга в малой окрестности таких сингулярностей сводится к ситуациям, иллюстрируемым рисунком 4.9.

Отрицательные (седловые) пассивные сингулярности обеспечивают топологическую связь между вихревыми сингулярностями с одинаковой хиральностью, в то время как соседние вихри с различным направлением прецессии вектора Умова – Пойнтинга соединяются линиями тока поперечной компоненты этого вектора непосредственно.

4.3. Сингулярности вектора Умова – Пойнтинга в векторных полях

4.3.1. Мгновенные сингулярности векторного поля

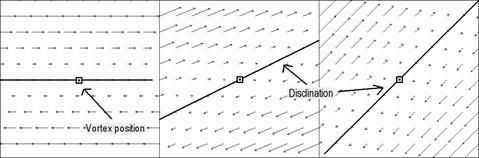
Аналогично скалярным полям и в соответствии с уравнением (4.1) – (4.3), мгновенные сингулярности вектора Умова – Пойнтинга возникают в точках поля, где наблюдается дисклинация или нуль поперечной компоненты этого вектора.

Как известно, дисклинации являются точечными дефектами векторного поля [3; 65]. Как было показано в пункте 3.1., дисклинации передвигаются вдоль -контуров, рождаются и исчезают. Количество их на -контуре может меняться только на четное число, т.е. как и все топологические дефекты, они возникают и пропадают только парами [3; 77]. Движение дисклинаций, их взаимосвязь, взаимосвязь с другими полевыми структурами происходит в соответствии с топологическими связями и закономерностями.

Поэтому события, ассоциируемые с сингулярностями вектора Умова – Пойнтинга, порожденными дисклинациями должны подчиняться аналогичным закономерностям.

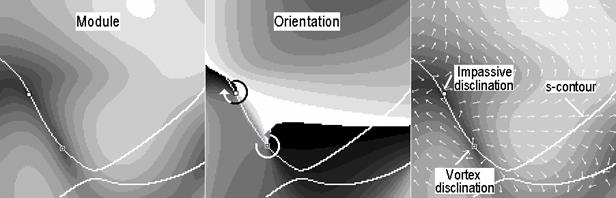
a b c

Рис. 4.10

Сингулярности вектора Умова – Пойнтинга, ассоциируемые с дисклинациями.

Случайное векторное поле.

a – мгновенное распределение модуля поперечной компоненты вектора Умова – Пойнтинга;

b – распределение мгновенного азимута поперечной компоненты. Разные оттенки серого соответствуют различной ориентации вектора; c – распределение модуля и азимута поперечной компоненты. Ориентация вектора Умова – Пойнтинга обозначена белыми стрелочками.

Из уравнений (4.1) – (4.3) не следует никаких ограничений относительно знака сингулярности, ассоциируемой с дисклинацией. Более того, положительные мгновенные дефекты вектора Пойнтинга могут быть как вихревыми, так и пассивными. Этот факт иллюстрируется результатами компьютерного моделирования (рис. 4.10).

Заметим, что такие вновь появившиеся дефекты могут быть оба вихревыми, т.е. обе сингулярности характеризуются одинаковыми индексами Пуанкаре и отличаются лишь хиральностью. Различие в хиральности достаточно для обеспечения связи между родившимися Пойнтинг-вихрями, но недостаточно для образования топологической связи с другими полевыми структурами.

Исходя из этого, возможны два сценария рождения и исчезновения сингулярностей вектора Умова – Пойнтинга, ассоциируемых с дисклинациями:

1. Представим себе, что на -контуре родились две вихревые сингулярности. Они обладают различной хиральностью, однако их индексы Пуанкаре одинаковые (позитивные). Исходя из закона сохранения суммарного топологического индекса, параллельно событию рождения этих сингулярностей в той же точке поля (на -контуре) должно произойти событие рождения двух отрицательных дефектов. Естественно, что это

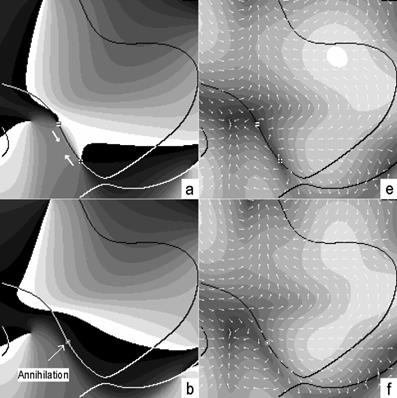
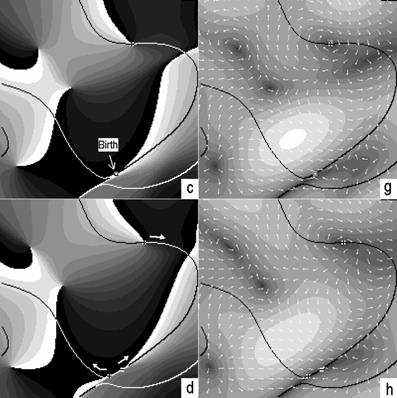
Рис. 4.11

Поведение сингулярностей вектора Умова – Пойнтинга, ассоциируемых с дисклинациями

для различных моментов времени.

a – d – распределение азимута поперечной компоненты вектора Умова – Пойнтинга. Разные оттенки серого обозначают различную ориентацию вектора. e – h – распределения модуля и азимута поперечной компоненты. Ориентация компоненты иллюстрируется тонкими белыми стрелками. Толстые белые стрелки на рисунках a, b, c, d указывают направление движения сингулярностей. , – позитивные и негативные мгновенные сингулярности вектора Умова – Пойнтинга соответственно. Сплошные линии - контура.

пассивные сингулярности, которые сразу же после акта рождения покидают -контур и уходят внутрь области эллиптической поляризации.

Как следствие, топологическая реакция, соответствующая этому событию, имеет вид:

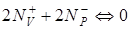, (4.9)

т.е. четыре дефекта поля поперечной компоненты вектора Умова – Пойнтинга появляются или исчезают.

2. Одна из сингулярностей, ассоциируемых с дисклинацией, позитивная, а вторая – отрицательная. В этом случае топологическая реакция возникновения – исчезновения трансформируется к следующему выражению:

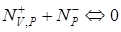. (4.10)

Только две сингулярности вектора Умова – Пойнтинга принимают участие в процессе.

Сингулярности вектора Умова – Пойнтинга, ассоциируемые с дисклинациями, как и сами дисклинации перемещаются вдоль -контура пропадают и рождаются (см. рис. 4.11). Их позиции повторяются через каждую половину периода колебания волны.

Рождение и аннигиляция сингулярностей может сопровождаться появлением и исчезновением дополнительных сингулярностей, когда только поперечная компонента вектора Умова – Пойнтинга равна нулю. В общем случае геометрическое место точек таких сингулярностей не находится на -контуре. Подобные сингулярности могут появляться независимо от рождения дисклинаций (рис. 4.12). При этом такие не связанные с -контуром сингулярности могут быть как пассивными, так и вихревыми.

Временное поведение мгновенной вихревой сингулярности, родившейся в области эллиптической поляризации, иллюстрируется рисунком 4.13. Как видно из рисунка, эта сингулярность перемещается через область с неоднородной поляризацией.

В заключение этого пункта отметим, что «мгновенный» усредненный по пространственным координатам и малому интервалу времени момент импульса поля, наблюдаемый в окрестности вихревой сингулярности, является максимальным по сравнению с моментами, возникающими в области других полевых структур (с той же энергией поля, сосредоточенной на таком же по размерам участке), независимо от того, порождена эта сингулярность дисклинацией или нет.

Рис. 4.13

Движение мгновенной вихревой сингулярности,

родившейся в области с неоднородной поляризацией.

4.3.2. Поведение вектора Умова – Пойнтинга в области элементарных поляризационных сингулярностей

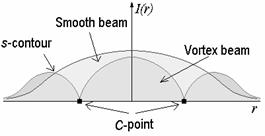Рассмотрим элементарную поляризационную ячейку – поле, содержащее минимальное количество (одну или две) -точки. Такие полевые образования с одной -точкой и методы их получения подробно рассмотрены в п. 3.5. Структура ячейки следующая. -точки одного или разных знаков помещаются в области с одним типом эллиптической поляризации (правая или левая), ограниченной -контуром относительно правильной формы. Как и поле с одной -точкой, поле с двумя -точками может быть сформировано с помощью суперпозиции вихревого циркулярно поляризованного пучка и ортогонально поляризованного гладкого. Можно показать, в случае суперпозиции циркулярно поляризованных волн -контур, как правило, замкнутый и ограниченных размеров.

Пример формирования элементарной поляризационно неоднородной ячейки иллюстрируется рис. 4.14.

Рассмотрение будем проводить при условии, что индексы -точек, распределение фазы и интенсивности в интерферирующих пучках могут меняться произвольным образом.

4.3.2.1. Симметричные распределения амплитуд и фаз интерферирующих пучков

а. Одна -точка

Предположим, что вихревой пучок циркулярно поляризованный изотропный вихрь:

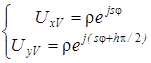, (4.11)

и ортогонально поляризованная к нему волна – плоская волна:

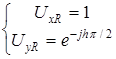, (4.12)

где 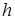– handedness фактор 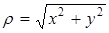; 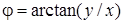– полярные координаты; 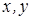– Декартовы координаты с началом в центре вихревого пучка; 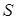– топологический заряд вихря.

Соответственно комплексные амплитуды результирующего поля имеют вид:

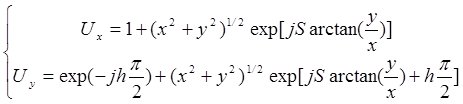; (4.13)

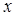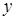- и -компоненты поля в терминах напряженностей описываются соотношениями

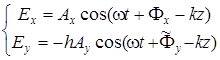, (4.14)

где

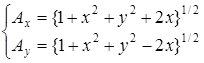, (4.15)

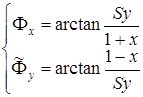. (4.16)

Можно показать, что в этом случае согласно (4.4) – (4.6):

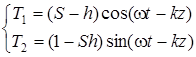(4.17)

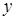Тогда для - и -компонент вектора Умова – Пойнтинга имеем

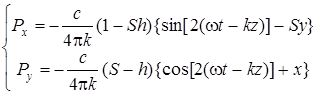. (4.18)

Соответственно модуль поперечной компоненты вектора Умова – Пойнтинга запишется так:

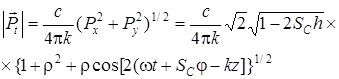, (4.19)

где 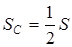– топологический заряд главной фазы (vibration phase) в окрестности -точки.

Дата добавления: 2015-07-12