Сети вихрей – скелетон фазы скалярного поля 11 страница

Координаты -точки могут быть определены как координаты точки в середине ловушки с постоянной интенсивностью для всех поляризационных проекций.

Таким образом, поляризационная ячейка с орбитальным моментом импульса, определяемым знаком топологического заряда вихревого пучка и практически неизменным по всей площади ловушки (области со значительной интенсивностью излучения) спиновым моментом импульса, была реализована. Именно энергия поля, заключенная в границах этой области, в основном влияет на характеристики вращения микрочастицы.

При этом плотность спинового момента импульса уменьшается от -точки по направлению к -контуру вследствие уменьшения эксцентриситета поляризационных эллипсов. Поэтому можно утверждать, что область в которой проявляется влияние спинового момента импульса, непосредственно прилегает к -точке и эта область по размерам значительно уступает размерам всей оптической ловушки. Поэтому изменение знака орбитального момента наиболее сказывается на характеристиках захваченного микрообъекта, по размерам сравнимого с размерами всей ловушки. Исходя из таких соображений, и были выбраны размеры микрочастиц (частицы в масле). Поведение захваченной ловушкой частицы иллюстрируется рисунками 4.33 и 4.34.

Захваченная частица вращается по часовой стрелке (рис. 4.33). Период вращения частицы составлял величину порядка 4 – 5 секунд.

Рисунок 4.34 соответствует ситуации, когда знак формирующего поляризационную ловушку вихря изменялся на противоположный, что соответствует изменению знака орбитального момента импульса. Частица вращалась против часовой стрелки со значительно меньшей скоростью. В этом случае период вращения составлял величину порядка 8 – 10 секунд. Различие между периодами вращения в первом и во втором случае может быть объяснено только тем, что в первой ситуации спиновый момент влияет на частицу в том же направлении, что и орбитальный, а при изменении топологического заряда -точки спиновый момент компенсирует орбитальный.

a) b) c) d)

Рис. 4.33

Вращение относительно большой прозрачной частицы благодаря орбитальному моменту импульса поля. Направление вращения по часовой стрелке.

a) b) c) d)

Рис. 4.34

Изменение направления и скорости вращения захваченной частицы благодаря изменению знака орбитального момента импульса.

a) b) c) d)

Рис. 4.35

Вращение маленькой поглощающей темной частицы, захваченной дифракционным кольцом, окружающем поляризационную ловушку. Вращение по часовой стрелке. Наиболее «яркая» часть светлого дифракционного кольца обозначена белой стрелкой на фигуре (b).

Следующий результат (рис. 4.35) иллюстрирует влияние орбитального момента импульса на маленькую поглощающую темную частицу, захваченную темным дифракционным кольцом, окружающим поляризационную ловушку. К сожалению, на рисунке видно только часть светлого дифракционного кольца, поскольку интенсивность в центре ловушки значительно превышает интенсивность кольца. Вдобавок интенсивность также сильно изменяется вдоль самого кольца. Как следствие – небольшой динамический диапазон CCD-камеры не позволил передать все градации интенсивности поля, соответствующего рисунку 4.35.

Видно, что частица вращается вдоль границы «главной» области ловушки. Такой характер вращения частицы можно объяснить только наличием орбитального момента импульса поля. Размер частицы составлял величину порядка 2-4 мкм. Период вращения 0.5 – 1 секунда.

В заключение этого параграфа акцентируем внимание читателя на характеристиках вращения частицы (рис. 4.33). Как следует из рисунка, центр вращения частицы явно не совпадает с центром световой ловушки. Это значит, что сингулярность вектора Умова – Пойнтинга смещена относительно позиции -точки (центр ловушки). Смещение сингулярности становится понятным, если обратиться к рисунку 4.31, из которого следует, что интерферирующие пучки обладали, по крайней мере, амплитудной асимметрией. Соответствеено, как показано в пункте 4.3.2.2, это должно было привести к смещению точки приложения максимального усредненного момента импульса поля.

Добавим, что существование орбитального момента импульса в окрестности -точки интересно не только с фундаментальной точки зрения, но может быть использовано и в прикладном аспекте для создания светлых поляризационных ловушек с контролируемым орбитальным моментом импульса поля.

4.3.3. Усредненный вектор Умова – Пойнтинга векторного поля

Как было показано в предыдущем пункте возникновение сингулярности усредненного вектора Умова – Пойнтинга в области элементарных поляризационных ячеек связано с наличием в этой области -точек с определенными характеристиками. Очевидно, что принципиально ничего не должно поменяться, если рассматривать возникновение сингулярностей этого вектора в поле общего вида.

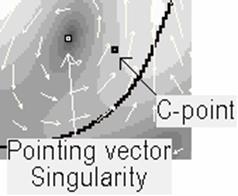
Иными словами, так или иначе, возникновение сингулярности вектора Умова – Пойнтинга ассоциируется с -точкой, находящейся около этого дефекта (см. рис. 4.36).

Тип сингулярности (вихревая или пассивная) зависит от соотношения знаков топологического заряда вибрационной фазы -точки и handedness фактора в области анализа. Вихревая сингулярность возникает, в случае если эти знаки разные:

. (4.27)

Пассивная сингулярность образуется, когда знак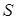и и одинаковые. Как следует из п. 3.1, связь между топологическим зарядом и индексом -точки имеет вид

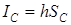. (4.28)

Тогда можно утверждать, что вихревая сингулярность поперечной компоненты вектора Умова – Пойнтинга соответствует -точкам с отрицательным индексом (или просто отрицательным -точкам) и пассивный дефект вектора возникает вблизи от позитивных -точек.

Этот факт иллюстрируется данными компьютерного моделирования, проведенного для случайного векторного поля (см. рис. 4.37). Видно, что поблизости от вихревых сингулярностей расположены отрицательные -точки. Пример такой ситуации обозначен на рисунке цифрами 1,1. Пассивные дефекты тяготеют к положительным -точкам (цифры 2,2).

Отметим, что вихревые сингулярности отличаются хиральностью. Тип хиральност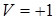и ( или 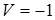) определяется знаком handedness фактора области, где расположена отрицательная -точка. Поперечная компонента вектора Умова – Пойнтинга циркулирует вокруг Пойнтинг-вихря по часовой стрелке в области с правой поляризацией (, 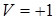) и она прецессирует в противоположном направлении в регионах с левой поляризацией (, ).

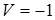В заключение этого раздела приводим две таблицы, в которых сведены основные свойства сингулярностей вектора Умова – Пойнтинга и их связь с традиционными оптическими сингулярностями.

Мгновенные сингулярности вектора Умова – Пойнтинга

Тип сингулярности вектора Умова – Пойнтинга	Краевая	Вихревые (В.С.) В.С.обладают одина-ковымтопологичес-ким индексоми отличаются хираль-ностью.	Пассивные (П.С.)
Скалярное поле	Локализация совпада-ет с эквифазными линиями	Не существуют	В процессе движенияП.С.обязательнопро-ходят через стаци- онарные точки фазы и интенсивности
Векторное поле	Не существуют	Как правило, В.С. совпадают с дискли- нациями	П.С.могут возникать независимо от дискли- наций

Усредненные сингулярности вектора Умова – Пойнтинга

Тип сингулярности вектора Умова – Пойнтинга	Вихревые (В.С.)	Пассивные (П.С.)
Скалярное поле	1. Локализация В.С. совпадает с вихрями поля. 2. Хиральность В.С.определяет-ся топологическим зарядом фазы вихря.	1. Позиции П.С. совпадают со стационарными точками фазы поля. 2. В дальнем поле П.С. в основном локализованы в седловых точках фазы.
Векторное поле	1. В.С. ассоциируется с отрица- тельными -точками. 2. Локализация В.С. и -точек в общем случае разная. 3. Хиральность В.С.опреде- ляетсяhandedness фактором области, в которой находитсяВ.С.	1П.С. ассоциируется с положи-тельными -точками. 2. Локализация П.С. и -точек в общем случае разная.

Дата добавления: 2015-07-12