Сети вихрей – скелетон фазы скалярного поля 7 страница

Результаты эксперимента иллюстрируется рисунком 3.27, на котором приведены интерферограммы линейно поляризованных проекций суммарного поля.

Шаг азимута анализатора 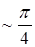. Рисунки a – d и рисунки e – h соответствуют различным разностям фаз 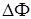между вихревыми пучками. Рисунки e – h иллюстрируют поведение вихря поляризационной проекции при разнице фаз между пучками, близкой к 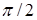. Как видно из рисунков, только один вихрь движется вдоль замкнутого -контура при изменении ориентации анализатора. Размеры и форма контура меняются при изменении разности фаз между пучками. Траектории следования вихря, его положение при каждом азимуте анализатора приведены на рисунках i, j. Отклонение формы -контура от окружности вызвано наличием остаточных аберраций и соответственно более сложной формой эквифазных линий поля фазы вихревых пучков. Эти же -контуры приведены на рисунках a и d.

Элементарные поляризационные структуры, возникающие при суперпозиции циркулярно поляризованных пучков, могут быть получены практически в той же схеме (рис. 3.25). Различие между схемами заключается в том, что пластинка 1 переставляется в опорную ветвь внешнего интерферометра, например, непосредственно за зеркалом 13. 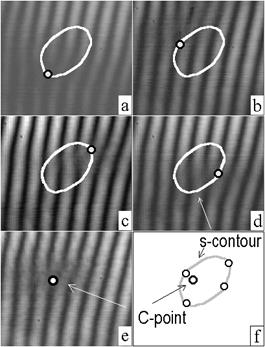Поляризаторы 8 и 12 убираются из схемы, а на их место устанавливаются две четвертьволновые пластинки, оси которых ориентированы так, что после них формируются право- и левоциркулярно поляризованные пучки. Синтезированная голограмма 3 устанавливается не после делителя 2, а располагается в одном из плеч интерферометра, например, после зеркала 11. Таким образом, в нижнем плече интерферометра формируется циркулярно поляризованный вихревой пучок, а в другом плече ортогонально поляризованный гладкий пучок.

Результаты моделирования приведены на рисунке 3.28. Рисунки a – d иллюстрируют сдвиг вихря поляризационной проекции суммарного поля вдоль -контура при вращении анализатора 18. Рисунок (е) интерференционная вилочка, указывающая на положение -точки, полученная при перекрытии канала внутреннего интерферометра, в котором формировался гладкий пучок. На рисунке (f) представлена -точка и 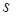-контур, восстановленный на основе экспериментальных данных. Как видно из рисунка, форма 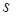-контура отличается от окружности и локализация -точки не совпадает с его центром. Этот факт можно объяснить остаточными аберрациями пучков и отклонением распределения интенсивности входного пучка от Гауссового.

3.7. Тонкая структура неоднородного векторного поля и его усредненные поляризационные характеристики

Поляризационные параметры, характеризующие световое поле, такие как матрица когерентности, параметры Стокса и т.д. [28; 80], исторически вводились для описания поляризационных характеристик некогерентного квазимонохроматического и т.д. пучков. В результате для получения данных параметров, в любом случае, проводится интегрирование измеряемых величин (их усреднение) по сечению пучка (пространственным координатам) и времени. Возникает вопрос. Можно ли вводить подобные локальные характеристики для произвольной точки в пространстве или во времени? Ответ на такой вопрос положительный, по крайней мере, для когерентных неоднородных полей [86 – 89; 98]. Естественно, что при взаимодействии света с веществом объекта когерентные характеристики пучка ухудшаются. Однако существует класс рассеивателей, которые изменяют когерентные характеристики незначительно, и уменьшение длины когерентности настолько мало, по сравнению с длиной когерентности современного лазера, что ею можно пренебречь. К таким объектам, например, относятся рассеиватели, реализующие однократное рассеяние (тонкие пленки и т. д.) [91], небольшие отрезки многомодовых оптических волокон [92] и пр.Другими словами, несмотря на то, что поле после взаимодействия с объектом формируется как спекл-поле, оно полностью поляризовано благодаря сохранению когерентности. В таком поле, в каждом спекле, поляризация меняется от точки к точке, проходя все состояния поляризаций, начиная от правоциркулярной до левоциркулярной поляризации. В то же время, характеристики векторного поля, к примеру, матрица когерентности и параметры Стокса, измеренные для всего пучка, будут аналогичны случаю, когда объект имеет деполяризующее действие.

Таким образом, можно сделать вывод о некой аналогии между поведением традиционных поляризационных параметров, измеряемых для пучков частично когерентного и даже некогерентного света, и аналогичных усредненных параметров, которыми можно описывать состояние поляризации целой области когерентного пучка. Этот вывод напрашивается хотя бы из того факта, что в большинстве физически реализуемых ситуаций возможна замена усреднения по времени на усреднение по пространственным координатам [59]. В силу линейности операций такого усреднения усредненные параметры Стокса, элементы матрицы когерентности есть простые интегралы по площади анализа от соответствующих локальных параметров.

Возникает вопрос. Как такие усредненные параметры взаимосвязаны со специфическими структурами векторного поля, такими как поляризационные сингулярности, области поля с седловыми точками поляризационных параметров, которые формируют скелетон поля (см. п. 3.1) и определяют поведение поля в каждой точке?

3.7.1. Усредненные параметры Стокса

Предположим, что лазерный пучок с достаточно большой длиной когерентности освещает рассеивающий объект, в общем случае со случайно распределенными оптическими характеристиками, центрами рассеяния, поверхностным рельефом и т.д. При этом объект относится к такому классу рассеивателей, которые практически не разрушают когерентные характеристики рассеянного поля, и в дальней зоне формируется когерентное случайное спекл-поле. Средние размеры спекла, в дальней зоне, как известно, определяются поперечными размерами светового пятна, сформированного непосредственно за объектом, расстоянием до точки наблюдения и длиной волны излучения [1; 2]. Поэтому измеряемые традиционными методами поляризационные характеристики поля так или иначе формируются на основе усредненных по площадке фотоприемника данных. При этом количество спеклов, помещающихся на площадке приемника, должно быть достаточно велико, чтоб усредненная величина мало отличалась от математического ожидания [93]. В противном случае измеряемая величина будет в той или иной мере случайной. Иными словами, для устойчивых измерений площадь приемника должна быть такой, чтоб она покрывала (в зависимости от требуемой точности измерения) 20 - 100 спеклов. Заметим, что в дальней зоне значения длин корреляций 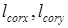(длин корреляции вдоль осей , 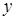лабораторной системы координат) для различных параметров поля (его интенсивности, фаз ортогональных компонент и т.д.) практически одинаковы. Поэтому под длиной корреляции поля 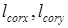будем понимать некие универсальные величины, не уточняя, к какой характеристике поля они относятся.

Таким образом, будем считать, что при измерении усредненных поляризационных характеристик векторного поля выполняется условие

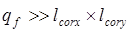, (3.65)

где 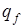– площадь фотоприемника, , .

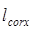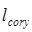Заметим, что в случае симметричного светового пятна после объекта, для достаточно широкого интервала углов рассеяния длинны корреляци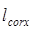й и 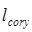практически равны. Более того, можно показать, что эти величины тождественно равны при ориентации лабораторной системы координат так, что выполняется условие:

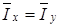, (3.66)

где, 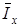, 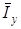– интенсивности ортогональных компонент, усредненные по площадке фотоприемника.

Естественно, что усредненные по площадке фотоприемника характеристики поля являются некоторой функцией угла освещения объекта и угла рассеяния, т.е. локальные характеристики поля, например интенсивность, распределены в области анализа неоднородно. Вместе с тем, в малом телесном угле ограниченным размером площадки фотоприемника можно с высокой точностью считать, что характеристики поля статистически однородны. При этом в большинстве случаев [2] статистика этих величин Гауссова. Различные отклонения от Гауссовой статистики подробно проанализированы в [74 – 76] и нами рассматриваться не будут.

В дальнейшем наше исследование будем проводить для некоторого фиксированного направления рассеяния. Поскольку именно условие (3.66) будет выполняться, то мы будем использовать лишь одну величину .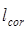

Сориентируем ось в выбранном направлении. Тогда можно констатировать, что справедливыми являются следующие утверждения:

1. Выполняется параксиальное приближение, если поперечные размеры светового пятна, непосредственно за рассеивающим объектом, и размеры площадки фотоприемника (площади анализа) намного меньше расстояния между объектом и областью наблюдения.

2. Поляризационную ситуацию поля в плоскости фотоприемника перпендикулярного к оси , можно описывать традиционными параметрами Стокса (как локальными 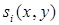, так и усредненными 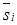, (i =0, 1, 2, 3)).

Известно [28; 80], что параметр Стокса 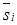можно получить, проводя измерения соответствующих интенсивностных параметров:

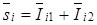. (3.67)

где, например, 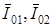– средние интенсивности - и 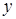-компонент поля и т.д.

Очевидно, что в случае измерения усредненных параметров 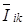– величина усредненная по площадке фотоприемника :

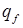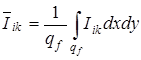, (3.68)

где 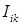– локальный интенсивностный параметр в произвольной точке области анализа. В дальнейшем, для простоты, множитель 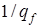будем упускать, так как он является постоянным и может быть всегда учтен соответствующей нормировкой.

3.7.2. Анализ усредненных параметров при разложении поля на линейно поляризованные компоненты

Известно [28; 80], что параметры Стокса (в том числе и локальные 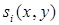) могут быть выражены через компоненты матрицы когерентности:

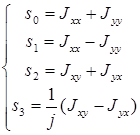. (3.69)

Заметим что 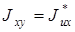(эрмитова матрица). Исходя из (3.68, 3.69) 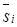выражается через усредненные компоненты матрицы когерентности:

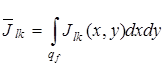, (3.70)

k,l =1, 2 – соответствуют x,y. Напомним [28], что:

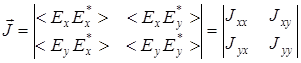, (3.71)

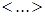– усреднение по времени.

При использовании когерентного, абсолютно поляризованного света усреднение по времени «снимается» и 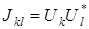, где 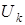– комплексная амплитуда ортогональных компонент. 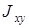имеет вид

,

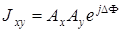где 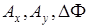– модули амплитуд и разность фаз ортогональных компонент.

Заметим, что выражение для 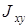совпадает с выражением для характеристической функции, введенной в п.3.2.2 (выражение (3.14)).

Поэтому вихри разности фаз можно трактовать как вихри недиагональных элементов матрицы когерентности. Нули 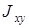совпадают с нулями компонент, которые, как было показано, однозначно связаны с поляризационными сингулярностями ( -контурами и -точками).

Усредненную компоненту матрицы когерентности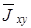

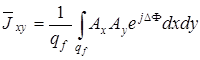(3.72)

можно интерпретировать как максимум корреляционной функции комплексных амплитуд ортогональных компонент [28]. Заметим, что 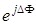быстро осциллирующая функция. При этом наибольшая скорость изменения 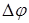наблюдается в районе нулей 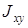(в областях вихрей компонент), где фаза компоненты изменятся от 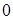до 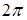в очень небольшой окрестности, включающей центр вихря. Там же, 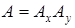– наименьшее (либо 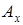, либо 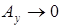). Как следствие, в результате интегрирования в соответствии с (3.72) вклад от таких областей в значение 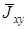минимальный. Основной вклад в величину 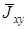осуществляют области стационарных точек 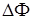, где производная от разности фаз меняется медленно. Поскольку в дальней зоне количество экстремумов разности фаз в 15 – 20 раз меньше (см. п.3.2.2), чем количество седловых точек этой величины, в дальнейшем, под стационарными точками разности фаз будем понимать именно ее седловые точки.

Соотношение (3.72) может быть аппроксимировано с помощью метода стационарной фазы [28; 94].

В области усреднения 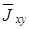может быть представлено как

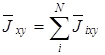, (3.73)

где

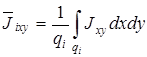, (3.74)

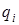– область, которая содержит одну стационарную точку разности фаз.

Для аппроксимации выражения (3.74) воспользуемся следующими рассуждениями, положенными в основу так называемого метода стационарных фаз [28].

Как известно, метод стационарных фаз дает возможность получить приближенное значение следующего интеграла:

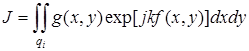. (3.75)

Обратимся к промежуточному выражению, на основе которого получена конечная формула метода стационарных фаз [28]:

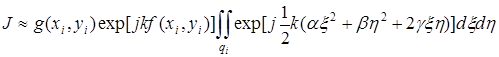, (3.76)

где 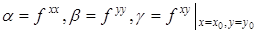, значения вторых производных от 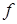в стационарной точке .

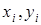Заметим, что в ситуации, рассматриваемой в этом параграфе

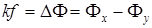. (3.77)

Соответственно, все вторые производные тоже разности производных, ассоциируемых с ортогональными компонентами:

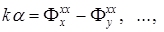и т.д. (3.78)

Теперь акцентируем внимание на следующих фактах:

i Ортогональные компоненты «сильно коррелированны» (во всяком случае, до уровней интегральной деполяризации порядка 50%. Этот факт, в частности, подтверждается данными компьютерного моделирования, приведенными ниже.

В таких условиях разности типа (3.78) минимизируются (характер изменения фазы компонент практически один и тот же).

ii В дальнем поле стационарные точки фазы расположены в центре спекла ортогональной компоненты. Как известно, именно там фаза практически постоянна (см. например, [1; 18]). Соответственно в области спекла, ограниченной вихрями компоненты изменяется в границах 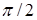[13; 25].

Исходя из этого, стационарные точки разности фаз, «спекла» разности фаз, ограниченном вихрями обоих компонент, также должны лежать в областях, где разность фаз 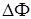меняется плавно в пределах того же порядка.

Тогда можно утверждать, что в силу соображений пунктов i и ii показатель экспоненты в подынтегральном выражении (3.76) невелик и экспонента практически равна единице. Соответственно, интеграл в (3.76) есть не что иное, как площадь анализа 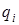и с точностью до множителя 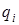соотношение (3.74) трансформируется к виду:

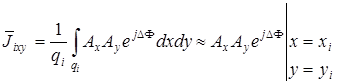, (3.79)

которое справедливо хотя бы для уровней деполяризации векторного поля до величины порядка 50%.

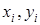в (3.79) находятся из условий:

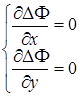, (3.80)

т.е. 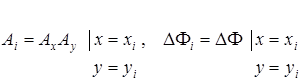– значения величин в точках седел разности фаз. В итоге 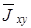может быть аппроксимировано выражением:

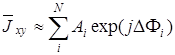. (3.81)

В соответствии с нашими предположениями, можно считать, что 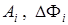в площади анализа – Гауссово распределенные случайные величины.

В общем случае среднее значение величины 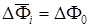( 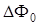– эффективная разность фаз между ортогональными компонентами) не равно нулю, т.е. 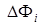– нецентрированная случайная величина. Представим 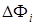как 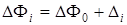. Соответственно случайная величина 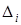распределена симметрично относительно 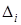=0. Плотность распределения 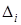– Гауссова:

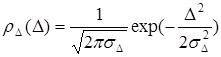, (3.82)

где 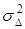– дисперсия фазы в седловых точках разности фаз.

Соответственно характеристическая функция имеет вид

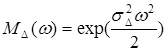. (3.83)

Сумма (3.81) может быть оценена как сумма случайных фазоров [2].

В соответствии с условием (3.66) (условия равенства средних интенсивностей ортогональных компонент), выберем ориентацию базиса разложения векторного поля.

Тогда

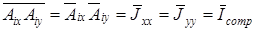, (3.84)

где – 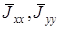усредненные по площади анализа интенсивности ортогональных компонент.

Из [2] известно, что для симметричных функций распределения :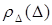

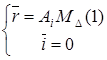, (3.85)

где 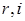– реальная и мнимая части суммы:

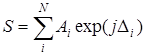. (3.86)

Из (3.84 – 3.86) имеем

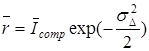. (3.87)

Тогда

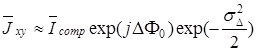. (3.88)

В этом случае параметры Стокса будут иметь вид

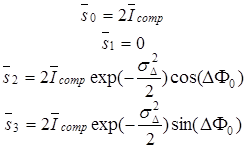, (3.89)

где 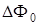– эффективная разница фаз ортогональных компонент.

Параметры Стокса, нормированные к единице, представляются в виде:

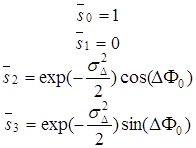. (3.90)

Естественно, что, как и в случае частично когерентного излучения, справедливо неравенство:

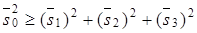. (3.91)

Наблюдается «интегральная деполяризация» и величина степени поляризации, рассчитанная в соответствии с соотношением:

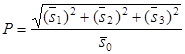, (3.92)

меньше единицы.

В нашем случае (3.92) трансформируется к выражению

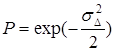. (3.93)

Равенство в (3.91) выполняется при 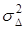=0 для однородно поляризованного поля. Как видим из (3.90), усредненные параметры Стокса определяются дисперсией разности фаз в седловых точках разности фаз.

Отметим, что 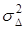связана с величиной среднего расстояния между ближайшими вихрями одного знака 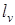, относящимся к разным компонентам. При полностью скоррелированных ортогональных компонентах (однородно поляризованное поле) 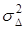и 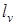=0 координаты нулей компонент полностью совпадают. При увеличении 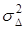, сетки компонентных вихрей не совпадают, и расстояние между такими вихрями начинает увеличиваться. Предельный случай 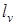= 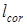– это полностью интегрально деполяризованное поле. Исходя из этих соображений, можно предположить, что 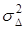является некоторой функцией : .

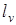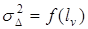Эта зависимость может быть получена, например, из данных компьютерного моделирования.

3.7.3. Компьютерное моделирование параметров векторного поля

Как было указано в предыдущем параграфе, рассмотрение проводится в дальней зоне и выполняется параксиальное приближение, поскольку анализ осуществляется для малого телесного угла и на значительном удалении от рассеивающего объекта. При наших условиях рассмотрения, длина корреляции поля не зависит от структуры рассеивающего объекта и определяется такими геометрическими параметрами, как «видимые» (в направлении данного угла рассеяния) поперечные размеры светового пятна, непосредственно за рассеивающим объектом, расстояние от рассеивающего объекта до области наблюдения и длина волны излучения.

Поскольку наше рассмотрение проводится в общем виде, то алгоритм компьютерного моделирования должен обеспечивать формирование векторных полей с требуемым набором усредненных параметров Стокса. Заметим, однако, что при выполнении условия (3.66) второй усредненный параметр Стокса всегда равен нулю. А при использовании нормированных параметров первый параметр Стокса всегда равен единице. Потому требования к алгоритму моделирования сводятся к требованию формирования векторных полей с требуемыми величинами третьего и четвертого параметров Стокса.

Отметим также, что в дальней зоне для фиксированного угла рассеяния и статистической однородности поля в площади анализа теряется непосредственная связь между характеристиками рассеянного поля и объектом рассеяния [91]. Иными словами, по данным (например параметрам Стокса), полученным для одного фиксированного угла рассеивания невозможно идентифицировать рассеивающий объект. «Одинаковые» поля соответствуют разным объектам. Поэтому в нашем случае в качестве рассеивающего объекта может быть использован любой объект, формирующий векторное поле с требуемыми параметрами Стокса. Это же утверждение касается и структуры линейно поляризованных ортогональных компонент. Иными словами, поле каждой компоненты должно представлять собой случайное скалярное поле общего вида. При этом должно выполняться условие (3.66) и алгоритм моделирования должен обеспечивать получение произвольного значения коэффициента корреляции 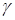между компонентами, что равносильно заданию требуемых величин третьего и четвертого параметров Стокса.

Известно, что при выполнении параксиального приближения поле в дальней зоне 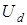, является Фурье-преобразованием поля сформированного непосредственно за рассеивающим объектом 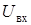[95]. По этому, учитывая, что структура поля в дальней зоне не связана со структурой объекта (за исключением требования случайности для поля 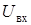), поле 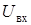для ортогональных компонент удобно формировать совокупностью хаотически расположенных точечных источников с единичной амплитудой и случайной фазой.

Дата добавления: 2015-07-12