
|
Читайте также: |
 , (3.94)
, (3.94)
 где
где  – количество точечных источников;
– количество точечных источников;  ,
,  – фаза и координаты
– фаза и координаты  -го точечного источника. Различие в формировании «входной» выборки точечных источников ортогональных компонент заключается лишь в том, что в выборках, соответствующих разным компонентам, некоторое количество точечных источников
-го точечного источника. Различие в формировании «входной» выборки точечных источников ортогональных компонент заключается лишь в том, что в выборках, соответствующих разным компонентам, некоторое количество точечных источников  полностью отличается как по фазе, так и по локализации.
полностью отличается как по фазе, так и по локализации.
В этом случае (в дальней зоне) будут сформированы компоненты с равной интенсивностью, а коэффициент корреляции компонент определяется простым отношением:
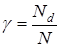 . (3.95)
. (3.95)
Уровень «интегральной деполяризации»  был выбран как поляризационный параметр, характеризирующий усредненные поляризационные характеристики векторного поля. Заметим, что поле остается полностью поляризованным в каждой точке. Известно, что при выполнении условия (3.66) интегральная деполяризация непосредственно связана с коэффициентом корреляции ортогональных компонент
был выбран как поляризационный параметр, характеризирующий усредненные поляризационные характеристики векторного поля. Заметим, что поле остается полностью поляризованным в каждой точке. Известно, что при выполнении условия (3.66) интегральная деполяризация непосредственно связана с коэффициентом корреляции ортогональных компонент 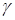 [28]:
[28]:
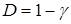 . (3.96)
. (3.96)
Поэтому в нашем случае 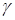 характеризует уровень поляризации при выполнении условия (3.66). Для разных уровней интегральной деполяризации были получены отношения расстояния между ближайшими компонентными вихрями
характеризует уровень поляризации при выполнении условия (3.66). Для разных уровней интегральной деполяризации были получены отношения расстояния между ближайшими компонентными вихрями  и длинны корреляции
и длинны корреляции 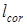 –
–  , карты разницы фаз и усредненные параметры Стокса.
, карты разницы фаз и усредненные параметры Стокса.
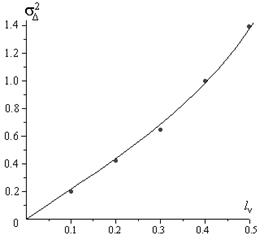
На рис. 3.29 представлена зависимость дисперсии разности фаз 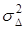 от среднего расстояния между ближайшими компонентными вихрями
от среднего расстояния между ближайшими компонентными вихрями  .
.
Для наглядности разность фаз представлена с точностью до  . Разности фаз, отличающиеся на
. Разности фаз, отличающиеся на  , обозначены одинаковым цветом. Границы между белыми и черными цветами –
, обозначены одинаковым цветом. Границы между белыми и черными цветами –  -контуры; точки, в которых сходятся линии всех цветов соответствуют вихрям разности фаз; точки в центре
-контуры; точки, в которых сходятся линии всех цветов соответствуют вихрям разности фаз; точки в центре  -образных областей – седловые точки разности фаз.
-образных областей – седловые точки разности фаз.

a b
Рис. 3.30
Карты разности фаз между ортогональными компонентами оптического поля для 40% деполяризации для эффективных разностей фаз 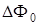 =0 (a) и
=0 (a) и  (b).
(b).
На рис. 3.30 приведены карты разности фаз для случаев эффективной разности фаз 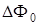 равной 0 и
равной 0 и  . Заметим, что характер поведения разности фаз не зависит от
. Заметим, что характер поведения разности фаз не зависит от 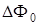 , поскольку разности фаз в обоих случаях в любой точке отличаются на постоянную величину. Следствием этого является изменение формы, размера и положения
, поскольку разности фаз в обоих случаях в любой точке отличаются на постоянную величину. Следствием этого является изменение формы, размера и положения  -контуров, в то время как седловые точки, вихри разности фаз своих позиций не меняют.
-контуров, в то время как седловые точки, вихри разности фаз своих позиций не меняют.
Очевидно, что  -контуры имеют наименьший размер (во всяком случае, для небольших уровней интегральной деполяризации), когда эффективная разность фаз
-контуры имеют наименьший размер (во всяком случае, для небольших уровней интегральной деполяризации), когда эффективная разность фаз 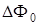 равна
равна  . Действительно, при небольших уровнях интегральной деполяризации область поля, непосредственно прилегающую к компонентным нулям, можно представить как суперпозицию практически одинаковых вихревых пучков. Как было показано в п. 3.5.1, минимальный размер
. Действительно, при небольших уровнях интегральной деполяризации область поля, непосредственно прилегающую к компонентным нулям, можно представить как суперпозицию практически одинаковых вихревых пучков. Как было показано в п. 3.5.1, минимальный размер  -контуров (сравнимый с расстоянием между центрами вихрей) наблюдается именно при разности фаз
-контуров (сравнимый с расстоянием между центрами вихрей) наблюдается именно при разности фаз 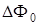 =
=  . Добавим, что полученный в этом пункте вывод о величине области, в которой поляризационные характеристики поля меняются значительно, также остается справедливым. Размеры таких областей в векторном поле с достаточно малой интегральной деполяризацией сравнимы с утроенным расстоянием между центрами вихрей.
. Добавим, что полученный в этом пункте вывод о величине области, в которой поляризационные характеристики поля меняются значительно, также остается справедливым. Размеры таких областей в векторном поле с достаточно малой интегральной деполяризацией сравнимы с утроенным расстоянием между центрами вихрей.

а b

c d
Рис. 3.31
Распределение интенсивности неоднородно поляризованного поля.
Распределение интенсивности для 5% (а), 10% (b), 30% (b), 50% (d) деполяризации поля (коэффициент корреляции ортогональных компонент 0.95, 0.9, 0.7, 0.5 соответственно).
Данные компьютерного моделирования подтверждают эти соображения. Как можно увидеть из рисунка 3.30 а,  -контуры имеют маленький размер и практически все смыкаются в площади рисунка, когда
-контуры имеют маленький размер и практически все смыкаются в площади рисунка, когда 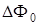 равна
равна  .
.
Результаты компьютерного моделирования интенсивности и разности фаз ортогональных компонент векторного поля для разных коэффициентов корреляции представлены на рис. 3.31, 3.32. Преимущественной была выбрана циркулярная поляризация. В этом случае, области со значительными поляризационными изменениями будут «совпадать» с областями, ограниченными  -контурами.
-контурами.

а b

c d
Рис. 3.32
Карты разности фаз между ортогональными компонентами.
Разность фаз между ортогональными компонентами для5% (а), 10% (b), 30% (c), 50% (d) деполяризации поля (коэффициент корреляции ортогональных компонент 0.95, 0.9, 0.7, 0.5 соответственно).
 – вихри
– вихри  -компоненты,
-компоненты,  – вихри
– вихри 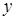 -компоненты.
-компоненты.
Распределение интенсивности полей слабо отличается для разных степеней деполяризации (см. рис. 3.31). Размер  -контуров и среднее расстояние между ближайшими соседними компонентными вихрями одного знака возрастают при увеличении уровня деполяризации (рис. 3.32).
-контуров и среднее расстояние между ближайшими соседними компонентными вихрями одного знака возрастают при увеличении уровня деполяризации (рис. 3.32).  -контуры маленькие (относительно среднего размера спекла) замкнутые области с одним типом поляризации (правоциркулярной или левоциркулярной) при коэффициенте корреляции больше чем 0.5. Эти зоны расположены очень близко к компонентным вихрям. Размеры
-контуры маленькие (относительно среднего размера спекла) замкнутые области с одним типом поляризации (правоциркулярной или левоциркулярной) при коэффициенте корреляции больше чем 0.5. Эти зоны расположены очень близко к компонентным вихрям. Размеры  -контуров увеличиваются и положение областей со значительными поляризационными изменениями стают случайными для значений коэффициента корреляции меньше чем 0.5.
-контуров увеличиваются и положение областей со значительными поляризационными изменениями стают случайными для значений коэффициента корреляции меньше чем 0.5.
3.7.4. Анализ усредненных параметров при Циркулярном базисе разложения поля
Как известно, структура  -,
-, 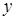 -компонент поля зависит от ориентации базиса разложения. В частности, в нашем рассмотрении, обязательным условием является такая ориентация базиса разложения, при которой интенсивности ортогональных компонент равны. С другой стороны, известно, что структура ортогональных компонент поля не зависит от ориентации базиса, если поле представлять как суперпозицию циркулярно поляризованных компонент. В этом случае разность фаз компонент напрямую связана с азимутом поляризации (3.3), а седловые точки разности фаз являются седловыми точками азимута. Поэтому проанализируем поле, как и в предыдущих параграфах, для такого базиса разложения.
-компонент поля зависит от ориентации базиса разложения. В частности, в нашем рассмотрении, обязательным условием является такая ориентация базиса разложения, при которой интенсивности ортогональных компонент равны. С другой стороны, известно, что структура ортогональных компонент поля не зависит от ориентации базиса, если поле представлять как суперпозицию циркулярно поляризованных компонент. В этом случае разность фаз компонент напрямую связана с азимутом поляризации (3.3), а седловые точки разности фаз являются седловыми точками азимута. Поэтому проанализируем поле, как и в предыдущих параграфах, для такого базиса разложения.
Матрица когерентности, полученная при разложении поля на циркулярно поляризованные составляющие, имеет вид:
 , (3.97)
, (3.97)
где  и т.д. (
и т.д. (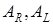 – модули амплитуд циркулярно поляризованных компонент являются случайными, пространственно распределенными величинами). В данном случае локализация вихрей разности фаз совпадает с позициями
– модули амплитуд циркулярно поляризованных компонент являются случайными, пространственно распределенными величинами). В данном случае локализация вихрей разности фаз совпадает с позициями  -точек (см. п. 3.1).
-точек (см. п. 3.1).
Параметры Стокса, выраженные через элементы такой матрицы, запишутся в следующем виде:
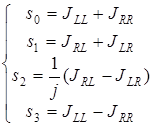 . (3.98)
. (3.98)
Осуществляя операции, аналогичные случаю линейного базиса, получаем следующие параметры Стокса:
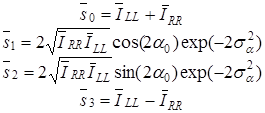 , (3.99)
, (3.99)
где  ,
,  – средние интенсивности левоциркулярной и правоциркулярной компонент соответственно;
– средние интенсивности левоциркулярной и правоциркулярной компонент соответственно;  – преимущественный азимут поляризации;
– преимущественный азимут поляризации;  – дисперсия азимута поляризации в его седловых точках.
– дисперсия азимута поляризации в его седловых точках.
Для циркулярного базиса, так же как и для линейного, справедливо неравенство:
 , (3.100)
, (3.100)
т.е. наблюдается так называемая «интегральная деполяризация». Равенство в (3.100) выполняется при 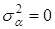 для однородно поляризованного поля. Как видим из соотношения (3.99), которое аналогично (3.89; 3.90), усредненные параметры Стокса могут быть определены на основе измерения дисперсии азимута поляризации в его седловых точках. Из этого же соотношения следует, что при известных параметрах Стокса простым вычислением может быть определена дисперсия азимута поляризации в областях с преимущественной поляризацией для неоднородно поляризованного векторного поля. Заметим, что дисперсия азимута в этом случае может быть представлена как функция расстояния между ближайшими вихрями одного знака
для однородно поляризованного поля. Как видим из соотношения (3.99), которое аналогично (3.89; 3.90), усредненные параметры Стокса могут быть определены на основе измерения дисперсии азимута поляризации в его седловых точках. Из этого же соотношения следует, что при известных параметрах Стокса простым вычислением может быть определена дисперсия азимута поляризации в областях с преимущественной поляризацией для неоднородно поляризованного векторного поля. Заметим, что дисперсия азимута в этом случае может быть представлена как функция расстояния между ближайшими вихрями одного знака  , относящимся к разным ортогональным линейно поляризованным компонентам.
, относящимся к разным ортогональным линейно поляризованным компонентам.
3.7.5. Сравнение экспериментальных результатов и данных компьютерного моделирования

 Параметры Стокса и среднее расстояние между ближайшими вихрями одного знака ортогональных компонент были получены не только в результате компьютерного моделирования, но и экспериментально определены для разных уровней деполяризации. В качестве тест-объектов были выбраны рассеивающие тонкие полимерные пленки. При этом деполяризации поля после рассеяния на них были близкими к уровням деполяризации, для которых проводилось компьютерное моделирование.
Параметры Стокса и среднее расстояние между ближайшими вихрями одного знака ортогональных компонент были получены не только в результате компьютерного моделирования, но и экспериментально определены для разных уровней деполяризации. В качестве тест-объектов были выбраны рассеивающие тонкие полимерные пленки. При этом деполяризации поля после рассеяния на них были близкими к уровням деполяризации, для которых проводилось компьютерное моделирование.
Схема экспериментального исследования представлена на рисунке 3.33. Циркулярно поляризованный пучок поступает на вход интерферометра Маха – Цандера. В одном из плечей интерферометра, в фокусе объектива 10 располагался рассеиватель (тонкая полимерная пленка). Такое экспериментальное положение обеспечивало, во-первых, анализ рассеянного поля в достаточно малом телесном угле и, во-вторых, обеспечивало формирование поля в дальней зоне с соответствующим масштабом спеклов, непосредственно после объектива. На выходе интерферометра располагался Стокс-поляриметр для измерения усредненных параметров Стокса. Циркулярно поляризованный опорный пучок и поляризатор 13 обеспечивали определение позиции и знака каждого компонентного вихря методом, описанным в [84,85]. При этом размер площадки фотоприемника удовлетворял неравенству (3.65). Таким образом, реализовывалась возможность одновременного измерения усредненных поляризационных параметров и получения сеток вихрей ортогональных компонент.
Компонентные вихри разных знаков можно идентифицировать из соответствующих интерференционных картин (см. рис. 3.34) как противоположно направленные интерференционные вилочки [8 – 10; 36 – 39]. В конечным итоге, были получены сети компонентных вихрей для разных объектов, которые вносили разный уровень деполяризации. А также были рассчитаны средние расстояния между соседними вихрями одного знака, относящихся к разным компонентам.
 На рисунке 3.35 и 3.36 представлены экспериментальные результаты и результаты компьютерного моделирования векторного поля для разных степеней деполяризации поля.
На рисунке 3.35 и 3.36 представлены экспериментальные результаты и результаты компьютерного моделирования векторного поля для разных степеней деполяризации поля.
 Рисунки 3.37 и 3.38 позволяют сравненить данные компьютерного моделирования и результаты эксперимента. На рисунке 3.37 представлена зависимость между уровнем деполяризации и отношением усредненного расстояния между вихрями к длине корреляции. Длина корреляции поля определялась из следующего соотношения:
Рисунки 3.37 и 3.38 позволяют сравненить данные компьютерного моделирования и результаты эксперимента. На рисунке 3.37 представлена зависимость между уровнем деполяризации и отношением усредненного расстояния между вихрями к длине корреляции. Длина корреляции поля определялась из следующего соотношения:
 , (3.101)
, (3.101)
где  – плотность вихрей любой ортогональной компоненты [9; 12].
– плотность вихрей любой ортогональной компоненты [9; 12].
Рисунок 3.38 иллюстрирует зависимость параметров Стокса 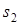 и
и  от отношения усредненного расстояния между компонентными вихрями одного
от отношения усредненного расстояния между компонентными вихрями одного
знака к длине корреляции.
Как видно, все зависимости практически линейны и наблюдается хорошее соответствие между данными, полученными компьютерным моделированием и экспериментальными исследованиями.
Таким образом, характеристики поляризационных сингулярностей, системы особых точек (вихрей разности фаз,  -точек, седловых точек разности фаз, азимута поляризации) определяют не только качественное
-точек, седловых точек разности фаз, азимута поляризации) определяют не только качественное
|

а b

c d

|
а b

c d




поведение векторного поля в каждой его точке, но и однозначно связаны с его усредненными поляризационными характеристиками.
Дисперсия разности фаз между ортогональными компонентами, соответствующая различным уровням интегральной деполяризации векторного поля, является функцией среднего расстояния между ближайшими вихрями одного знака, относящимся к разным линейно поляризованным ортогональным компонентам. В конечном итоге, усредненные параметры Стокса, дисперсия азимута поляризации могут быть получены при измерении такого среднего расстояния.
Размеры областей, в которых существенно меняется поляризация, определяются только уровнем интегральной деполяризации. Размеры и положение  -контуров для уровня деполяризации менее 50% зависят также и от эффективной разности фаз между компонентами. Размеры
-контуров для уровня деполяризации менее 50% зависят также и от эффективной разности фаз между компонентами. Размеры  -контуров минимальны при преимущественной циркулярной поляризации векторного поля. Для уровня деполяризации более 50% структура поля становится аналогичной структуре полностью деполяризованного поля и не зависит от эффективной разности фаз между ортогональными компонентами.
-контуров минимальны при преимущественной циркулярной поляризации векторного поля. Для уровня деполяризации более 50% структура поля становится аналогичной структуре полностью деполяризованного поля и не зависит от эффективной разности фаз между ортогональными компонентами.
3.8. «Стокс-формализм» поляризационных сингулярностей. «Стокс-вихри».
Как было показано, в п. 3.2.3, поляризационные сингулярности могут быть однозначно идентифицированы с помощью интерференционного метода, который является особенно эффективным в зонах поля, где его интенсивность мала. Например, в случае слабо «деполяризованных» полей, когда зоны со значительными поляризационными изменениями тяготеют к зонам нулей ортогональных компонент. В такой ситуации анализ структуры векторного поля на основе интенсивностных измерений (параметров Стокса и т.д.) становится проблематичным. Вместе с тем, для полей, степень интегральной деполяризации, которых достаточно велика (более 40 – 50%), локализация поляризационных сингулярностей не связана напрямую с зонами малой интенсивности поля, и поляризационные сингулярности могут быть идентифицированы в результате анализа локальных традиционных поляризационных параметров поля [86 – 89].
Поэтому, с нашей точки зрения, было бы полезным связать поляризационные сингулярности с поведением таких характеристик векторного поля.
Предположим, что в результате экспериментальных исследований нами получен полный набор параметров Стокса (для простоты нормированных) в каждой точке поля.
Одна из записей нормированных параметров Стокса когерентного поля имеет вид [98; 99]:
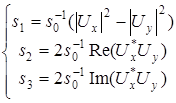 , (3.102)
, (3.102)
При этом имеет место равенство
 . (3.103)
. (3.103)
Рассмотрим так называемые Стокс-поля 
 , определяемые соотношениями [98]:
, определяемые соотношениями [98]:
 . (3.104)
. (3.104)
Естественно, что такого типа поля характеризуются системой сингулярностей. Эти сингулярности будем называть Стокс-вихрями [98].
Координаты Стокс-вихрей поля  , как и обычных скалярных вихрей, могут быть найдены как решения системы уравнений:
, как и обычных скалярных вихрей, могут быть найдены как решения системы уравнений:
 . (3.105)
. (3.105)
Из (3.102, 3.103) следует, что в точках Стокс-вихрей только один из параметров Стокса остается ненулевым. Более того, его величина по модулю равна 1.
Так, например, для вихрей поля 
 , а
, а  . Из этого следует, что вихри поля
. Из этого следует, что вихри поля  совпадают с
совпадают с  -точками. Введем для описания вихрей поля
-точками. Введем для описания вихрей поля  дополнительный параметр
дополнительный параметр 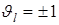 , определяющий знак ненулевого параметра Стокса. Тогда вихрь поля
, определяющий знак ненулевого параметра Стокса. Тогда вихрь поля  с
с 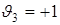 (
( ) соответствует
) соответствует  -точке, локализованной в области с правой (левой) поляризацией.
-точке, локализованной в области с правой (левой) поляризацией.
Аналогично для поля 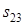
 , т.е. вихри поля
, т.е. вихри поля 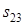 совпадают с вихрями компонент (вихрями разности фаз), поскольку либо
совпадают с вихрями компонент (вихрями разности фаз), поскольку либо  , либо
, либо  равны нулю.
равны нулю.
Обратимся вновь к соотношению (3.105). Решения первого и второго уравнений определяют системы некоторых замкнутых контуров. Так, из (3.102) легко видеть, что для поля  первое уравнение определяет контура, вдоль которых интенсивности компонент одинаковы, а решения второго уравнения формируют систему
первое уравнение определяет контура, вдоль которых интенсивности компонент одинаковы, а решения второго уравнения формируют систему  -контуров (см. п.3.22).
-контуров (см. п.3.22).
Для поля 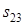 решения аналогичных уравнений соответствуют системам
решения аналогичных уравнений соответствуют системам  - и
- и  -контуров. Иными словами, вихри этого поля, как и вихри разности фаз (вихри недиагональной компоненты матрицы когерентности
-контуров. Иными словами, вихри этого поля, как и вихри разности фаз (вихри недиагональной компоненты матрицы когерентности 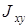 ), находятся на их пересечении. Действительно, легко показать, что
), находятся на их пересечении. Действительно, легко показать, что
 . (3.106)
. (3.106)
И, наконец, вихри поля  (
(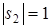 ) возникают на пересечении
) возникают на пересечении  -контуров и линий, вдоль которых интенсивности компонент одинаковы. Очевидно, что вихри поля
-контуров и линий, вдоль которых интенсивности компонент одинаковы. Очевидно, что вихри поля  не соответствуют ни одному типу традиционных поляризационных сингулярностей и определяют координаты «реперных» точек
не соответствуют ни одному типу традиционных поляризационных сингулярностей и определяют координаты «реперных» точек  -контура, в которых азимут линейной поляризации
-контура, в которых азимут линейной поляризации  либо
либо  .
.
Естественно, что, используя «стокс-формализм», можно сформулировать различного вида знаковые принципы, касающиеся вихрей разности фаз или  -точек и достаточно просто получить различного рода топологические инварианты типа (3.50).
-точек и достаточно просто получить различного рода топологические инварианты типа (3.50).
4. Сингулярности вектора Умова – Пойнтинга и структура оптических полей
Естественным вопросом, у человека, читающего эту книгу, является вопрос: каковы резоны рассмотрения сингулярностей вектора Умова – Пойнтинга?
Попробуем ответить на этот вопрос, отталкиваясь от уже полученной информации о «традиционных» оптических сингулярностях: фазовых вихрях, поляризационных сингулярностях.
Первое, на чем необходимо акцентировать внимание это то, что в области оптической сингулярности поле «абсолютно» гладкое, без «разрывов» и удовлетворяет уравнениям Максвелла. Так, в центре фазового вихря (скалярной сингулярности) неопределенность фазы, вообще говоря, не имеет смысла, поскольку модуль амплитуды равен нулю и значение фазы может быть любым.

 Аналогичные соображения можно привести и в отношении поляризационных сингулярностей
Аналогичные соображения можно привести и в отношении поляризационных сингулярностей  -контуров и
-контуров и  -точек. Действительно, если на некотором расстоянии от
-точек. Действительно, если на некотором расстоянии от  -точки поворот осей эллипсов поляризации реально характеризует отличие в поляризационных характеристиках поля, то в непосредственной близости от «сингулярности» эллипсы мало отличаются от окружностей (см. рис. 4.1) и понятия азимута, главной фазы, также как понятие фазы в центре вихря, теряют смысл. Иными словами, такие параметры как главная фаза, азимут, не нужны для описания состояния поля в
-точки поворот осей эллипсов поляризации реально характеризует отличие в поляризационных характеристиках поля, то в непосредственной близости от «сингулярности» эллипсы мало отличаются от окружностей (см. рис. 4.1) и понятия азимута, главной фазы, также как понятие фазы в центре вихря, теряют смысл. Иными словами, такие параметры как главная фаза, азимут, не нужны для описания состояния поля в  -точке, а направление вращения вектора поля «лишняя» характеристика для точек
-точке, а направление вращения вектора поля «лишняя» характеристика для точек  -контура. К тому же временное поведение вектора поля в
-контура. К тому же временное поведение вектора поля в  -точке (на
-точке (на  -контуре) и рядом практически неразличимы. Традиционными оптическими измерениями невозможно различить точки, принадлежащие сингулярному множеству, и точки его окрестности. Такие области на рисунке 4.1 схематически изображены как регионы
-контуре) и рядом практически неразличимы. Традиционными оптическими измерениями невозможно различить точки, принадлежащие сингулярному множеству, и точки его окрестности. Такие области на рисунке 4.1 схематически изображены как регионы 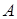 и
и 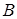 .
.
Дата добавления: 2015-07-12; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сети вихрей – скелетон фазы скалярного поля 7 страница | | | Сети вихрей – скелетон фазы скалярного поля 9 страница |