Фазовые вихри.

Поскольку параметры спекл-полей характеризуются комплексными функциями самого общего вида, то логично предполагать, что им свойственны различного рода особенности – как точечные, так и протяженные. Такие особенности сингулярности, стационарные точки объединяются в системы – сети [3 – 25]. Эти сети как некий остов-скелетон формируют структуру поля, а информация о характеристиках таких множеств дает возможность предсказать поведение поля (хотя бы на качественном уровне) в любой его точке.

Размах исследований в этой области достиг такой величины, что можно утверждать, что в классической оптике, занимающейся, прежде всего, изучением закономерностей распространения электромагнитных волн, формированием оптических полей, их структуры и характеристик, сложилось новое направление «сингулярная оптика».

Необходимо отметить, что основные принципы этого направления сформулированы в блестящей книге профессора Джона Ная «Natural focusing and fine structure of light», вышедшей в 1999 году [3]. Поэтому вопросам, подробно рассмотренным в [3], в предлагаемой читателю книге, возможно уделено недостаточно внимания, поскольку она задумывалась как некоторое (автору хотелось бы надеяться, успешное) дополнение к этой великолепной работе.

Именно поэтому в книге сделан акцент на «решающей» роли сингулярностей различного типа при формировании структуры электромагнитного поля. Автору хотелось бы надеяться, что его видение проблем сингулярной оптики, преимуществ сингулярного подхода при решении оптических задач, роли сетей сингулярностей как скелетона электромагнитного поля будет интересно не только ему, но и другим исследователям, занимающимся проблемами современной оптики.

Для того, чтобы сделать материал книги и затрагиваемые в ней вопросы обозримыми, автор сознательно ограничился рассмотрением строго монохроматических волн. Не анализируются также сингулярности волн, возникающие в оптических волноводах, нелинейных средах и т.д., поскольку это предмет для отдельной серьезной книги.

В заключение заметим, что в последнее время количество публикаций, посвященных сингулярной оптике, лавинообразно нарастает, поэтому список цитируемой в книге литературы может показаться неоправданно коротким. Особенно это относится к заключительному разделу, посвященному сингулярностям вектора Умова – Пойнтинга.

Вместе с тем, по мнению автора, список цитируемой литературы содержит все основные (принципиальные) публикации, касающиеся главных аспектов роли сингулярностей в электромагнитных полях.

Основные понятия скалярной сингулярной оптики.

Фазовые вихри.

Как известно (см. например, 12; 28), однородно поляризованная когерентная волна общего вида, с частотой 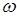, , свободно распространяющаяся в пространстве, удовлетворяет волновое уравнение

, (1.1)

где и – длина волны излучения. Среди множества решений этого уравнения существует решения, для которых выполняется соотношение:

, (1.2)

где 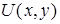– комплексная амплитуда поля, а – единичный вектор, задающий состояние поляризации волны. Величина 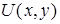удовлетворяет уравнение Лапласа

. (1.3)

Решением этого уравнения является любая аналитическая функция комплексного переменного, простейшая из которых:

(1.4)

При этом удовлетворяет волновое уравнение (1.1). Соотношение (1.4) может быть легко преобразовано к виду, который является традиционной записью комплексной амплитуды:

, (1.5)

где – модуль амплитуды и 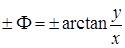– составляющая фазы, определяемая пространственными координатами. Как следует из (1.5), величины и могут быть также интерпретированы как полярные координаты с в точке . Как видим, модуль амплитуды такой волны стремится к 0, а фаза не определена при условии, что . Иными словами в точке наблюдается сингулярность фазы. Такая волновая структура получила название дислокации волнового фронта или оптического вихря [3 – 39]. Учитывая, что в дальнейшем, кроме подобных вихрей будут рассматриваться вихри различной природы, будем называть такие вихри фазовыми.

Распределение фазы в области вихря (фазовая карта), заданного уравнением (1.4), иллюстрируется рисунком 1.1 a.

Как видим, при обходе центра вихря по окружности фаза нарастает или спадает в зависимости от знака (+) или (–) в (1.4) линейно. В работе [12] такие вихри получили название изотропных. В общем случае (рис. 1.1 с) эквифазная линия, соответствующая нулевой фазе, может и не совпадать с осью лабораторной системы координат, привязанной к центру вихря. Величину фазового сдвига в дальнейшем будем называть начальной фазой изотропного вихря. Заметим, что изменение фазы (рис. 1.1 с) можно получить из распределения (рис. 1.1 а) простым поворотом системы координат на угол величиной .

a b с

Рис. 1.1

Фазовая карта изотропного вихря. Изменение оттенка серого соответствует изменению фазы. a) – соответствует знаку (+) в уравнении (1.4); b) – знаку (–). с) – изменение фазы при обходе вихря. Сплошная линия на рис. (с) – позитивный вихрь (+ в выражении (1.4)). Пунктирная – отрицательный.

Естественно, что для реального поля уравнение (1.4) выполняется крайне редко. Область, в которой изменение фазы описывается линейным приближением, будем называть [3; 4] ядром вихря. Как правило, изменение фазы в области ядра вихря описывается нелинейным законом (см. рис. 1.2 и 1.3), что соответствует появлению в (1.4) действительных коэффициентов перед 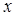и 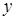(рис. 1.2). Наиболее общий случай распределения фазы вихря возникает при дополнительном повороте фазовой структуры вихря на некоторый угол (рис. 1.3 a). 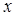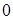Как видим из рисунка, нулевая линия фазы не совпадает с осью , а угол между эквифазными линиями и 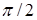не равен 90^о. Такие вихри получили название анизотропных. К общим свойства изменения фазы при обходе вихря произвольного вида надо отнести следующее:

1. Фазовая поверхность в окрестности вихря – правый или левый геликоид. Только в этом случае реализуется прирост или убыль фазы на величину 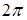при полном обходе центра вихря.

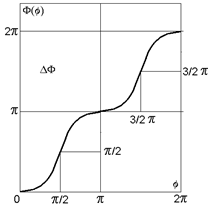
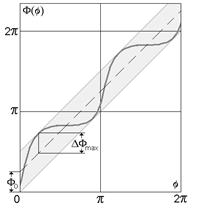
2. Изменение фазы как функция полярного угла имеет монотонный характер (рис. 1.3 b). Именно поэтому любому анизотропному вихрю может быть поставлен в соответствие изотропный [25]. Будем называть такой изотропный вихрь характеризующим. Изменение фазы характеризующего вихря обозначено на рисунке пунктирной линией. При этом максимальное отличие фазы реального вихря и фазы характеризующего вихря не превышает 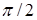. Иными словами, по критерию Релея, любой анизотропный вихрь, с точностью до 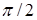, может быть заменен изотропным вихрем с определенным значением начальной фазы .

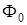a b с

Рис. 1.2

Фазовая карта анизотропного вихря.

a b

Рис. 1.3

Замена анизотропного вихря на изотропный.

3. При переходе через центр вихря фаза скачком изменяется на . Благодаря этому характер изменения фазы на соседних участках, в точках, отличающихся по полярному углу на величину одинаков и при этом выполняется условие – .

1.2. Топологический заряд и топологический индекс особых точек. Элементарные топологические реакции.

В этом пункте рассмотрим топологические характеристики сингулярностей и стационарных точек поля фазы, а также элементарные топологические реакции их рождения и исчезновения.

1.2.1. Топологический заряд

Особые точки какой-либо величины принято характеризовать топологическими индексами двух типов [11]. Первый из них, так называемый топологический заряд, вводится для особой точки (например, для особой точки поля фазы), исходя из следующего соотношения:

(1.6)

где интегрирование проводится по небольшой окружности (по направлению против часовой стрелки), описанной около особой точки.

Легко видеть, что для изменения фазы
(рис. 1.1 – 1.3) – топологический заряд равен + или – 1. Знак (+) соответствует ситуации, когда при обходе вихря против часовой стрелки фаза нарастает и (–) – если фаза спадает. В общем случае возможно и другое поведение фазы, при котором топологический заряд по модулю может быть больше единицы и равен 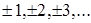. Однако можно показать, что вихри с топологическим зарядом по модулю, большим единицы, топологически и физически неустойчивы и даже при небольшом физическом возмущении распадаются на систему простых единичных вихрей. Поэтому в дальнейшем, будем считать, что в оптическом (по крайней мере, в случайном) поле реализуются лишь вихри с зарядом .

Легко показать, что для областей поля, которые не содержат сингулярную точку (включая и стационарные точки), .

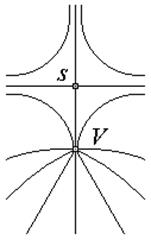
На рисунке 1.4 схематически изображены эквифазные линии поля в области вихря (точка 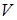) и седловой точки . Поскольку топологический заряд присущ только области поля, включающей вихрь, то топологический заряд участка поля, изображенного на рисунке, равен + или – 1.

1.2.2. Топологический индекс

Топологический индекс второго типа – так называемый индекс Пуанкаре (в дальнейшем просто индекс). Вычисляется он следующим образом. При обходе особой точки следят, в какую сторону вращаются линии, характеризующие полевую структуру, образованную в ее окрестности (например эквифазные линии). Если направление вращения линий совпадает с направлением обхода, то полевой структуре присваивается индекс со знаком (+); если линии вращаются в противоположную сторону, то индексу присваивается знак (–). Модуль индекса равен количеству полных оборотов линий, которое подсчитывается при возвращении в начальную точку. Так, исходя из рисунка 1.4, на котором представлены эквифазные линии участка поля, включающего вихрь 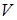и седловую точку , можно сделать вывод, что как позитивный, так и негативный вихри характеризуются одним индексом , а седловая точка индексом 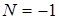. Экстремумы фазы, как и вихри, характеризуются индексом .

1.2.3. Закон сохранения топологического заряда.

Можно показать, что для некоторой области, содержащей особых точек могут быть введены суммарные топологический заряд и индекс [11]. В силу свойств Эвклидова пространства, выполняется закон сохранения суммарных топологического заряда и индекса, который для оптического поля может быть сформулирован следующим образом. Любое возмущение оптического поля не приводит к изменению суммарных топологического заряда и индекса. При этом, если электромагнитная волна свободно распространяется в линейной среде и на ее пути не встречаются источники и абсолютно поглощающие стоки, то величины 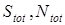остаются постоянными для любого сечения поля [11].

1.2.4. Элементарные топологические реакции.

Исходя из закона сохранения топологических заряда и индекса, появление в поле отдельного вихря невозможно, поскольку при этом будет меняться (увеличится или уменьшится на 1) значение суммарного топологического заряда . Поэтому рождение вихрей (или их исчезновение) всегда происходит как рождение (или исчезновение) пары вихрей с топологическими зарядами разных знаков . Это утверждение получило название «парного принципа».

Одновременно с этим появление двух вихрей приводит к изменению суммарного топологического индекса 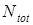вследствие того, что вихри, независимо от знака обладают положительным индексом Пуанкаре .

Соответственно появление двух вихрей обязательно должно сопровождаться рождением двух дополнительных седел с отрицательным индексом .

Фактически такой элементарный процесс может быть описан следующей топологической реакцией [11]:

, (1.7)

где – положительный, отрицательный вихри и седло фазы соответственно.

Исходя из этого топологического уравнения, оценим относительное количество топологических элементов, которые могут возникать в поле.

Свернем неограниченную по пространству плоскость наблюдения в сферу с бесконечным радиусом. Начнем с топологически реализуемой ситуации, когда на этой сфере, в поле существуют только два вихря противоположного знака, и будем постепенно увеличивать их количество. В соответствии с реакцией (1.7), приходим к следующим соотношениям между количеством топологических элементов:

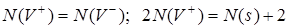. (1.8)

Когда количество вихрей в поле достаточно большое двойкой в последнем выражении можно пренебречь.

1.3. Экспериментальное наблюдение и идентификация вихрей скалярного поля.

Поскольку в центре вихрей интенсивность поля равна нулю, то наиболее простой способ идентификации вихрей поля может быть основан на измерениях его интенсивности. Однако измерения интенсивности не могут дать однозначного ответа: вихрь, поля наблюдается в точке или близкий к нулю минимум интенсивности. Это связано с тем, что в отличие от поля фазы, где вихри проявляются как сингулярные точки, в поле интенсивности они всего лишь стационарные точки. Как следствие распределение интенсивности в области вихря аналогично распределению области обычного минимума.

В то же время, особенности поведения фазы в зоне вихря приводят к тому, что при интерференции такой полевой структуры, например с плоским опорным пучком, наблюдается разделение интерференционной полосы, образуется так называемая интерференционная вилочка (см. рис. 1.5)
[8 – 10; 12; 14; 29 – 31; 36 – 39]. Причем направление вилки определяется знаком топологического заряда вихря.

Таким образом, интерференционные вилочки, сформированные вихрями разных знаков, разнонаправлены.

Необходимо отметить, что если вихревой или опорный пучок имеют дополнительную кривизну, то при осевой интерференции вместо вилочек наблюдаются спирали (см. рис. 1.6) Знак вихря (в данном случае ) определяется направлением «закрутки» спирали.

На рисунке 1.7 представлены результаты интерференции вихря с топологическим зарядом и сферической опорной волны для различных углов между пучками.

Из вышесказанного следует вывод, что единственными надежными методами идентификации вихрей являются методы интерферометрии. Более подробно об интерференционной идентификации вихрей см., например, в [36 – 38].

Рис. 1.7

Угол между вихревым и опорным пучком возрастает от рисунка a к рисунку f. Рисунок a соответствует осевой интерференции.

1.4. Генерация вихрей с помощью синтезированных голограмм.

Абсолютно очевидно, что устройство, с помощью которого можно генерировать вихри, может быть выполнено в виде голограммы, распределение пропускания которой имеет вид подобный изменению интенсивности, предсталенному на рис. 1.5.

Рассмотрим интерференцию вихревого пучка с плоской опорной волной [36 – 38]. Пусть для определенности вихревой пучок – изотропный вихрь с положительным топологическим зарядом:

, (1.9)

а плоская волна составляет угол с осью :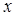

. (1.10)

Тогда интенсивность результирующего поля имеет вид

. (1.11)

Предположим, что зафиксированное на фотоносителе распределение интенсивности формирует амплитудное пропускание

, (1.12)

где коэффициенты отражают нелинейность записи голограммы.

Легко показать, что с учетом (1.11) соотношение (1.12) примет вид:

, (1.13)

где коэффициенты 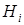также отражают нелинейность записи голограммы,
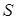– номер дифракционного порядка голограммы.

Из (1.13) следует, что при освещении голограммы плоской опорной волной в направлениях будут восстанавливаться вихревые пучки с топологическим зарядом . Например, во втором дифракционном порядке (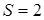) восстановится вихрь с двойным отрицательным топологическим зарядом [37].

2. Вихри и структура фазы скалярного поля.

2.1. Знаковый принцип

В п. 1.2.4 предыдущего раздела мы проанализировали процессы рождения и исчезновения сингулярных структур поля фазы. Сформулированный на этой основе парный принцип [11] имеет фундаментальный характер, но он не дает ответа, какой из пары родившихся вихрей (+), а какой (–). В роботе [13] сформулирован принцип, который получил название знакового принципа, закрывающий этот пробел.

Рассмотрим комплексную амплитуду некоторого случайного одномерного сигнала [8]. Изменения его действительной и мнимой частей в зависимости от 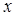схематически представлены на рисунке 2.1. а.

a b

Как следует из рисунка, в общем случае точки, в которых и равны нулю, не совпадают. Отсюда следует вывод, что одномерный комплексный сигнал никогда не достигает нулевого значения.

Ситуация в корне меняется для двумерной комплексной функции. Точки, в которых и равны нулю, вытягиваются в линии
(рис. 2.1. b). Для простоты будем называть их линиями . Они замкнутые и односвязные, хотя в общем случае допускаются и самопересечения.

В итоге координаты вихрей (нулей поля) могут быть найдены как решения системы [3; 4; 8]:

. (2.1)

Каждое из уравнений определяет систему эвифазных линий (линий постоянной фазы) и соответственно. Пересечение этих линий и есть позиции вихрей поля.

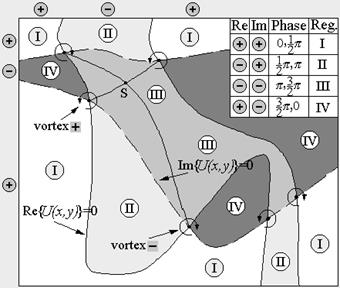
Суть принципа можно легко понять, если обратиться к рисунку 2.1 b, на котором область случайного поля разбита на участки, в границах которых с точностью до 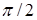фаза постоянна. Участки ограничены линиями , линиями, которые являются решениями уравнений системы (2.1).

Исходя из рисунка, формулировка знакового принципа может быть следующей [13]:

Соседние вихри, лежащие на одной и той же линии , должны быть противоположного знака.

Заметим, что понятие лини постоянной фазы с ее «конкретным» значением в оптике достаточно условно, поскольку реальный физический смысл вследствие быстрых изменений поля имеет лишь разность фаз, которая может быть зафиксирована экспериментально, например, с помощью методов интерферометрии.

При этом очевидно, что вихри разных знаков можно соединить целым пучком эквифазных линий, в то время как соседние вихри одного знака соединяются непосредственно всего одной линией постоянной фазы, проходящей через седловую точку (см. рисунок).

Поэтому формулировка знакового принципа может быть уточнена следующим образом:

Если соседние вихри могут быть соединены линией постоянной фазы, которая не проходит через седло, то такие вихри имеют разные знаки топологических зарядов. В противном случае такие вихри одного знака.

Это общий принцип, которому не свойственны ограничения и он может быть использован для всех типов волновых полей.

Как простое использование этого принципа рассмотрим участок линии , или , на котором находятся два соседних вихря () и () со знаками (+) и (–) соответственно. Если между этими вихрями появляется новая пара вихрей , , 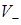то знаковый принцип требует, чтобы новая конфигурация имела вид ()()(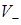)(). В то же время парный принцип допускает еще одну конфигурацию ()()()()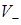, которая запрещена.

Заметим, что парный принцип – это правило, которое справедливо для отдельно взятой точки комплексной волновой функции, и как следствие – является локальным принципом. В то же время знаковый принцип устанавливает связь между разными точками волновой функции и поэтому является глобальным (относящимся ко всему полю) принципом. Соответственно, знаковый принцип не может быть сведен к парному принципу. С другой стороны, значительное количество следствий парного принципа можно автоматически получить как прямые следствия знакового принципа.

Можно сформулировать три основных следствия знакового принципа:

(1). Знак отдельного произвольного вихря волнового поля автоматически фиксирует (определяет) знаки всех остальных вихрей волнового поля.

(2). Если знак одного из вихрей поля, находящегося в любой его точке, изменяется, то знаки всех других вихрей меняются автоматически.

(3). Знак первого вихря, родившегося в процессе эволюции волнового поля, определяет знаки вихрей, которые будут рождены в будущем.

2.2. Фазовые спеклы. «Дыхание» фазовых спеклов

Введем понятие «фазового спекла» [25]. Фазовым спеклом (рис. 2.2) будем называть пространственный, структурный элемент поля фазы, ограниченный линиями , и их пересечениями (вихрями), которые образуют односвязную замкнутую линию. Необходимо отметить, что положение линий , определено с точностью до постоянного фазового множителя комплексной амплитуды поля. Неподвижными элементами фазового спекла являются вихри – узлы спекла и стационарные точки фазы. В качестве

Рис.2.3

«Дыхание» фазовых спеклов

Фазовые спеклы поучены в результате компьютерного моделирования. Каждый следующий рисунок отличается от предыдущего постоянным фазовым множителем на 0.05 . На рисунках представлено положение линий и , отличающееся оттенком серого. В зависимости от интервала, в котором изменяется фаза (в каждом спекле изменение фазы осуществляется в границах p /2), фазовые спеклы обозначены оттенками серого и белым. Средняя фаза в спекле возрастает соответственно плотности серого цвета.

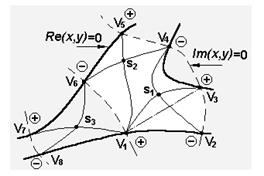
фазового множителя одинакового для всего поля может быть рассмотрен временной фазовый множитель или множитель 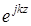, описывающий распространение волны вдоль оси . При этом, в зависимости от 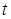или , линии , осуществляют пространственное колебание от одного седла фазы к другому. Рисунок 2.3 иллюстрирует такое «дыхание» фазовых спеклов. Фазовые спеклы соответствуют полю в дальней зоне и получены в результате компьютерного моделирования. Шаг изменения фазы постоянного фазового множителя от рис. 2.3 a до рис. 2.3 j составляет 0.05 . Наибольшая скорость сдвига линий , в зависимости от изменения постоянной фазы поля наблюдается в районе стационарных точек поля фазы, наименьшая – в зоне относительно больших градиентов фазы – между седлами.

2.3. Физическая реализуемость (генерисити) и структурная стабильность дефектов поля.

Заметим, что вихри не единственные сингулярные структуры скалярных полей, описанные в литературе (см., например, [3; 4; 14]). Кроме вихрей, достаточно часто рассматриваются такие образования как краевые дислокации волнового фронта [3; 4], представляющие собой «протяженные» в плоскости анализа нулевые дефекты (нулевые поверхности или замкнутые нулевые линии, хотя бы часть которых лежит в плоскости анализа). Однако существование таких (подобных) дефектов поля напрямую связано с физической реализуемостью полевой структуры, так называемой «генерисити» (genericity). Понятие генерисити вводится в [3] и указывает на то, что генерик-объекты – это структурностабильные (в пространстве и времени) естественные реализации определенных моделей физических объектов без дополнительных ухищрений экспериментатора. Естественно, что при определенных воздействиях на физический процесс (например, при специфической модуляции фазы поля или его части и т.д.) в некоторой точке (области) поля может возникнуть нонгенерик-структура хотя бы потому, что ее возникновение и существование не противоречит уравнениям Максвелла и другим фундаментальным уравнениям и понятиям теории электромагнитного поля.

Однако продолжительность существования такой структуры занимает точку на оси времени. Причем свойства поля в рассматриваемой точке (области) пространства «до рождения» и «после исчезновения» такого специфического полевого образования кардинально, драматически отличаются от свойств поля в момент реализации структуры.

Исходя из этлго, нельзя говорить ни о «продолжительности возникновения, существования, исчезновения» структуры, ни о «величине» физического воздействия. Время существования (появления, распада) структуры и величина воздействия бесконечно малы. Поэтому вероятность одновременной реализации хотя бы двух нонгенерик-структур нулевая.

Исходя из этого, можно утверждать, что в фиксированной плоскости наблюдения для любого поля и любого физического воздействия, в данный момент времени может существовать лишь одна и только одна нонгенерик-структура как «точечно-временной» дефект поля.

С понятием генерисити тесно связано другое понятие – понятие структурной стабильности полевой структуры. Единичный вихрь поля, группа вихрей одного знака являются абсолютно стабильными полевыми объектами, поскольку для их исчезновения необходимо осуществление специального процесса – аннигиляции. Полевая структура из двух близко расположенных вихрей, структура в окрестности точки аннигиляции вихрей являются генерик-ситуациями, но структурно нестабильны, поскольку возникновение относительно небольшого возмущения поля может привести к распаду таких полевых образований. Заметим, что наблюдение процесса распада полевых структур жестко привязано к положению плоскости анализа. В этом смысле, «точечность» структуры, возникающей в окрестности точки аннигиляции, приводит к ее абсолютной нестабильности относительно плоскости анализа, поскольку ее смещение в пространстве обусловлено сколь угодно малым возмущением поля.

В заключение отметим, что, исходя из сказанного, существование краевой дислокации (протяженного нулевого дефекта), на наш взгляд, является проблематичным.

a b c

Рис. 2.4

Возникновение такого дефекта предполагает существование в пространстве либо «нулевой» поверхности, либо нулевой линии, хотя бы часть которой совпадает с плоскостью анализа. Очевидно, что существование нулевой поверхности является абсолютно нереализуемой ситуацией и может быть рассмотрено лишь как определенная модель, например, в случае близко расположенных неразличимых экспериментально нулевых линий, траектории которых мало отличаются (рис. 2.4 a). Сечение такой «поверхности» (обозначенной на рисунке литерами 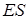) плоскостью представляет собой цепочку близко расположенных вихрей. В то же время возникновение замкнутой линии, вдоль которой поле равно нулю – генерик случай. Однако для существования краевой дислокации дополнительно требуется, чтобы хотя бы часть этой линии совпадала с плоскостью анализа. Именно при касании участка этой линии и плоскости наблюдения возникает краевая дислокация (см. рис. 2.4 b, зона А). Вместе с тем, абсолютное совпадение отрезка линии, вдоль которого поле равно нулю, и плоскости, ориентированной каким бы то ни было образом, представляется нам физически нереализуемой ситуацией. Иначе говоря, существование нулевой линии такого типа – нонгенерик-случай. На самом деле можно показать, что точка касания нулевой линии и плоскости анализа может быть лишь одна, а в остальных случаях нулевая линия пересекает плоскость наблюдения и образует систему близко расположенных вихрей (рис. 2.4 c – увеличенное изображение зоны А). Точка касания нулевой линии обозначена литерами .

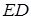Можно показать, что интерференционная картина, возникающая при суперпозиции такой структуры с регулярным опорным пучком аналогична интерференционной картине, присущей краевой дислокации. Именно поэтому структуру, возникающую в точке аннигиляции вихрей, будем называть «краевой дислокацией нулевой длины».

2.4. Рождение вихрей

1. В роботе [9] представлены результаты экспериментальных исследований процессов рождения дислокаций волнового фронта (измерения их плотности) в зависимости от расстояния до рассеивающего объекта.

2. Для наглядности рассмотрим рассеивающий объект, который вносит только фазовую модуляцию (объект типа матовое стекло). Тогда непосредственно за рассеивающим объектом модуляция поля чисто фазовая и вихри в граничном поле отсутствуют [40]. Очевидно, вихри возникают в ближней зоне вследствие многолучевой интерференции, как только поле приобретает модуляцию не только по фазе, но и по амплитуде.

3. Как показано в [9], процесс возникновения вихрей, увеличение их количества происходит скачкообразно (рис. 2.5) и практически к началу зоны Френеля плотность нулей (с точностью до угловой расходимости поля) достигает своего конечного значения и остается постоянной вплоть до бесконечности.

4. На рисунке 2.6 схематически изображен процесс развития трехмерной спекл-структуры поля. Так называемая зона тени, область , в которой спекл-поле только формируется, и есть зона возникновения вихрей. При этом нельзя утверждать, что эволюция вихрей в области Френеля не отличается от распространения вихрей в дальней зоне. В области Френеля тело спекла имеет более или менее правильную «эллипсовидную» форму. Размеры спекла (в том числе и продольные) конечны и увеличиваются по мере приближения к зоне Фраунгофера. При этом границы спекла, в частности его сечение, может описываться односвязными замкнутыми кривыми достаточно сложной формы [41 – 43]. Линии нулей поля, их траектории располагаются вдоль границы спекла и также являются замкнутыми односвязными кривыми. При перемещении плоскости анализа вдоль можно наблюдать рождение, распространение и аннигиляцию вихрей поля. Точка рождения пары нулей возникает в точке касания этой плоскости к нулевой линии, обвивающей тело спекла (точка, обозначенная на рисунке литерой ). 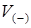При дальнейшем перемещении плоскости вдоль для любого ее положения наблюдаются два вихря и вплоть до точки, в которой наблюдается очередное касание плоскости анализа и нулевой линии (точка ). Здесь вихри аннигилируют [41]. Иначе говоря, при перемещении плоскости анализа вдоль эволюцию вихрей поля в зоне Френеля (при постоянной их средней плотности) можно рассматривать как процесс постоянного рождения и исчезновения пар вихрей. В этом смысле динамика сеток вихрей в этой области изменения коренным образом отличается от эволюции вихрей в дальней зоне. Здесь нулевые линии замыкаются на бесконечности. Поэтому с некоторого момента количество актов аннигиляции и рождения новых пар вихрей начинает уменьшаться, и, в конечном итоге, эти явления прекращаются. Образуются практически стационарные (с точностью до углового коэффициента) сети вихрей поля.

5. Таким образом, зародившиеся в результате многолучевой интерференции вихри в дальней зоне не аннигилируют.

6. Несмотря на то, что механизм возникновения вихрей очевиден – это интерференция парциальных волн (см., например, [38; 11 – 13]), конкретный механизм их появления остается неясным. С нашей точки зрения, физическая природа этого явления может быть следующей. Поскольку основное количество вихрей возникает между объектом и зоной Френеля, где преобладает фазовая модуляция поля, то поле, образующееся в процессе распространения волны в этой зоне, можно получить, пользуясь приближением волновых фронтов (см. Аппендикс 2). Таким образом, в создании вихрей принимают участие только соседние участки волнового фронта, а вкладом от интерференции с волнами, сформированными вторичными источниками, расположенными на некотором расстоянии от зоны возникновения вихря, можно пренебречь. Тогда процесс появления вихря можно интерпретировать как интерференцию малого количества парциальных волн с приблизительно одинаковыми интенсивностями и относительно гладкими волновыми фронтами.

Принципы формирования сетки дислокаций при интерференции трех плоских волн и Гауссовых пучков рассмотрены в [44 – 46]. Однако, на практике, реально интерферирующие волны могут быть рассмотрены как плоские или Гауссовы лишь как определенного вида приближения. Поэтому рассмотрим возникновение вихрей при интерференции волн общего вида.

2.5. Возникновение дислокаций волнового фронта вследствие интерференции волновых фронтов с простыми фазовыми поверхностями

Рассмотрим интерференцию минимального количества (двух) произвольных когерентных волн и 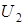[47; 48]. Фазы этих волн , , и модули амплитуд , такие, что для каждой плоскости наблюдения, перпендикулярной к оси , задающей основное направление распространения волн, каждую из них можно рассматривать в рамках приближения волновых фронтов (см. Аппендикс 2). Иными словами, можно считать, что волны и распространяются в зоне анализа «без дифракции». В точке 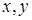плоскости наблюдения модули амплитуд полей мало отличаются, и существует решение уравнения в виде – линии равных интенсивностей (модулей амплитуды поля).

Условие возникновения изолированного нуля суммарного поля в точке 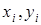имеет вид

. (2.4)

Проанализируем результирующее поле, созданное волнами и . Введем локальную систему координат с началом координат в точке -го нуля амплитуды. Направление оси совпадает с направлением оси . Разложим результирующее поле в ряд Маклорена по степеням и , ограничившись только линейными членами. Легко показать, что результирующее поле может быть записано в виде:

, (2.5)

где , , , , , .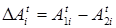

Тогда тангенс фазы результирующего поля в окрестности -го нуля результирующего поля опишется соотношением:

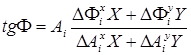. (2.6)

Из (2.6) следует, что поле в окрестности нуля не что иное, как винтовая дислокация волнового фронта. Знак вихря определяется соотношением между и , т.е. соотношением градиентов модулей амплитуд и градиентом фаз интерферирующих пучков.

Проанализируем связь между «фазами» вихрей результирующего поля. По аналогии с начальной фазой изотропного вихря (см. п.1.1), фазой вихря будем называть некоторую постоянную фазу в окрестности ядра вихря, которая может быть определена для каждой точки окрестности как постоянная «подставка» к изменяющейся составляющей фазы. Как и в случае изотропного вихря, именно эта фаза определяет интенсивность интерференционной картины в окрестности нуля поля («темная», «светлая» или «серая» вилка). Введем параметр , задающий положение точки вдоль линии равных интенсивностей. Результирующее поле вдоль этой линии описывается соотношением

. (2.7)

В точке 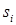, точке пересечения линии равных интенсивностей с 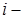тым минимумом интерференционной картины, показатель экспоненты определяет фазу вихря. Учитывая (2.5), из (2.7) получаем, что эта фаза описывается соотношением:

(2.8)

Подчеркнем, что координата может быть связана с фазовой поверхностью любого из двух фронтов. Очевидно, что показатель экспоненты остается неизменным при обходе точки 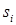в плоскости 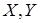на небольшом расстоянии от точки 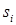. Разница между фазами в соседних минимумах интерференционной картины равна

. (2.9)

Из (2.9) вытекает, что фазы в двух соседних точках 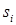отличаются на . При наложении на такое поле опорной волны интерференционные вилочки, соответствующие таким сингулярностям, будут отличаться по цвету, т.е. если первая вилочка образуются разделением темной интерференционной полосы, то вторая вилочка формируется разделением светлой.

Пусть обе волны практически плоские и направлены так, что линия пересечения фронтов параллельна оси , и фронты волн наклонены относительно плоскости 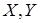под углами, одинаковыми по модулю
(рис. 2.7). При этом интенсивности волн меняются в направлении , а вдоль оси они постоянны.

Тогд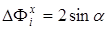а , , а .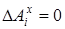

Соответственно (2.6) преобразуется к виду

. (2.10)

Из (2.10) следует, что поскольку , а , то знак коэффициента перед отношением и соответственно знаки вихрей определяются только знаком величины . Более того, если интенсивность одной из волн постоянна, то знаки вихрей определяются направлением возрастания интенсивности во второй волне.

Этот факт подтверждается данными компьютерного моделирования (рис. 2.8), где представлены результаты интерференции двух квазиплоских, близких по интенсивности волн и зондирующего опорного пучка. Вертикальные полосы картины соответствуют результирующему полю с образовавшимися вихрями. Горизонтальные – результат суперпозиции этого поля и опорного пучка. Характер изменения интенсивности интерферирующих волн схематически представлен на рисунках 2.8 e – g. Линии равных интенсивностей на рисунках (a) – (c) обозначены стрелками.

Как видно из рисунка (a), в соседних интерференционных минимумах наблюдаются вихри одного знака. Соответствующие зоны выделены прямоугольниками c литерами А и B. Фазы вихрей в соседних минимумах отличаются на . Хорошо видно, что вилочка, выделенная квадратом А – «черная», она как будто вложена в «белую» вилочку, обозначенную квадратом В. Характер изменения интенсивности волн иллюстрируется рисунком (e).

Экспериментально полученная цепочка подобных вихрей иллюстрируется рис. 2.9.

На рисунках 2.8 b, c наблюдаются две системы интерференционных разнонаправленных вилочек в соответствии с характером изменения интенсивности волн, представленном на рис 2.8 f. Вихри с разным знаком топологического заряда выделены квадратами A и B. Отметим, что особенности интерференционной картины постепенно сглаживаются, разнонаправленные вилочки становятся все труднее различимыми при уменьшении расстояния между такими вихрями. Наконец, вихри аннигилируют на рисунке (g). В этом случае возникает особая точка фазы, которая может быть интерпретирована как «краевая дислокация нулевой длины». Можно показать, что топологический заряд области, включающей такой дефект поля , а индекс . Таким образом, реально реакция аннигиляции по сравнению с соотношением (1.7) происходит в два этапа:

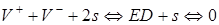. . (2.11)

Сначала аннигилируют вихри и образуется краевая дислокация нулевой длины. При этом два седла сливаются в одно и лишь после этого «складка» фазы разглаживается:

. (2.12)

В итоге процесс аннигиляции можно рассматривать как следующую цепочку: разрушение вихрей как более «мощных» сингулярностей, имеющих ненулевой топологический заряд, а затем окончательное исчезновение особенности поля [49 – 52]. Заметим, что такая цепочка абсолютно не противоречит закону сохранения суммарных топологических заряда и индекса, поскольку на каждом этапе эти величины остаются постоянными.

Экспериментально ситуацию интерференционного образования вихрей можно смоделировать практически в любом интерферометре, в том числе и в интерферометре сдвига. На основе интерферометра сдвига появляется возможность формирования интерференционного преобразователя «гладкий пучок – сингулярный» [53].

В качестве интерферометра сдвига был использован стеклянный клин, грани которого образуют небольшой угол 3’’ 5’’. При освещении такой пластинки
He-Ne-лазером в направлении на отражение наблюдается интерференционная картина с достаточно большим периодом (порядка нескольких миллиметров), т.е. интерферирующие пучки практически не расходятся. На заднюю поверхность пластинки был напылен тонкий отражающий слой аллюминия (рис. 2.10) с коэффициентом отражения, близким к 100%. При напылении передней поверхности были созданы такие условия, что коэффициент отражения плавно менялся вдоль рабочей области – практически от 0 до 100%. При этом изменения пропускания осуществлялись в направлении, перпендикулярном к направлению интерференционных полос. В итоге отраженные от передней грани (пучок 1) и от задней грани (пучок 2) пучки приобретали модуляцию интенсивности (рис. 2.10 b). Таким образом, создавались необходимые условия для интерференционного возникновения вихрей. Результаты тестирования преобразованного пучка представлены на рис. 2.10 с.

2.6. Топологические индексы поля интенсивностей. Экстремумы фазы и интенсивности, «корреляция» фазы и интенсивности

Необходимо отметить, что в то время как топологические заряды присущи только вихревым полям, индекс Пуанкаре N может быть введен и для градиентных полей [25]. Введем топологические индексы поля интенсивности, следя, как изменяется направление линий тока градиента интенсивности в окрестности стационарных точек. Экстремумы, в том числе и нули амплитуды, как абсолютные минимумы интенсивности поля характеризуются индексом N =+1, седлам интенсивности может быть присвоен отрицательный индекс N =-1. Соответственно, рождение (исчезновение) экстремума должно сопровождаться появлением (исчезновением) седла интенсивности, обеспечивающего топологическую связь экстремума с другими полевыми структурами и другими экстремумами. Хотя вихри и максимумы интенсивности не отличаются по значению индекса N, все же можно сделать некоторые выводы об их количественном соотношении. Из простых соображений вытекает: если в некоторой области определения любой физической величины существует экстремум, то в этой же области должен существовать хотя бы один противоположный экстремум. Применяя подход, аналогичный описанному в [11], приходим к выводу, что минимальное количество максимумов и седел интенсивности подчиняется соотношению:

, (2.13)

где – минимальное количество максимумов, – количество вихрей поля, – минимальное количество седловых точек интенсивности.

Теперь рассмотрим вопрос, сколько вообще может быть экстремумов фазы и интенсивности.

В роботах [11; 24] в предположении, что комплексная амплитуда поля в дальней зоне описывается соотношением

(2.14)

(т.е. зависимость комплексной амплитуды от определяется постоянным фазовым множителем), получена система:

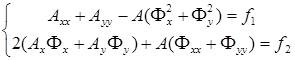, (2.15)

где 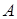– модуль амплитуды; 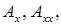...и т.п. – частные производные первого и второго порядков от модуля амплитуды и фазы, а правая часть уравнений f₁, f₂ =0.

Легко видеть, что из второго уравнения (2.15) следует вывод о невозможности существования фазовых экстремумов в дальней зоне. Действительно, для точек экстремума фазы второе уравнение системы (2.15) преобразуется к виду

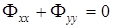, (2.16)

которое заведомо не выполняется, поскольку в экстремальных точках вторые производные всегда одного знака.

Однако при анализе первого уравнения приходим к еще более удивительному выводу: в дальней зоне невозможны максимумы интенсивности. Действительно, рассмотрим возможность появления в поле максимумов интенсивности. В этих точках =0, а . Тогда сумма первых двух слагаемых первого уравнения всегда меньше нуля. Выражение в скобках всегда больше нуля. Таким образом, в точках максимума интенсивности левая часть первого уравнения не может равняться нулю. Это явное противоречие, поскольку наличие в поле нулей амплитуды предполагает, как минимум, столько же максимумов интенсивности. Из этого следует, что в нашем случае для анализа поля в дальней зоне допущение (2.14) неприемлемо.

Об этом свидетельствуют также результаты, полученные в ряде работ [21; 24] при непосредственном компьютерном моделировании случайных полей. Авторы утверждают, что даже в дальней зоне формируются, правда в небольшом количестве, экстремумы и несимметричные седла фазы (на 14 – 20 вихрей приходится приблизительно один дополнительный экстремум фазы).

Попробуем снять это противоречие, вытекающие из анализа соотношения (2.15), опираясь на следующие утверждения.

1. Поскольку рассматриваемое нами поле, поле электромагнитное, то в общем случае напряженность электрического поля, комплексная волновая функция всегда векторные величины. Строго говоря, рассматривать его как скалярное можно только в случае, если выполняется параксиальное приближение.

2. Фурье-приближение может оказаться слишком грубым при анализе процессов формирования тонкой структуры поля. Поэтому необходимо использовать более «мягкое» приближение – приближение Френеля (или близкое к нему).

Запишем комплексную амплитуду поля на некотором расстоянии от входной плоскости, которое соответствует зоне дифракции Френеля:

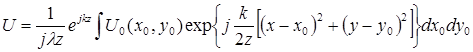, (2.17)

где 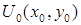– граничное поле.

Для нахождения явного вида U будем считать, что область изменения значительно меньше области, в которой меняются 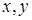, что достаточно часто реализуется на практике. Иными словами, размеры зоны анализа поля намного больше, чем поперечные размеры рассеивающего объекта. В этом случае фазовым множителем можно пренебречь, и (2.17) приобретает вид:

, (2.18)

Дата добавления: 2015-07-12