
|
Читайте также: |
2.7.1. Восстановление фазы поля на основе «сдвинутых» «сеток нулей».
Пусть поле 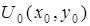 характеризуется определенной амплитудной (задано некоторое «изображение») и случайной фазовой модуляцией. Соответственно в дальней зоне формируется случайное поле
характеризуется определенной амплитудной (задано некоторое «изображение») и случайной фазовой модуляцией. Соответственно в дальней зоне формируется случайное поле  , которое определяется Фурье-образом поля
, которое определяется Фурье-образом поля  .
.
Известно, что поле 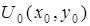 может быть восстановлено (или восстановлен близкий к
может быть восстановлено (или восстановлен близкий к  образ) с помощью Шенноновской выборки, сформированной из отсчетов поля в плоскости
образ) с помощью Шенноновской выборки, сформированной из отсчетов поля в плоскости  , если
, если  – функция с ограниченным спектром (или выборка отсчетов формируется в области, где сосредоточена основная энергия поля
– функция с ограниченным спектром (или выборка отсчетов формируется в области, где сосредоточена основная энергия поля  ) [59]. Максимальный шаг между отсчетами (в оптической интерпретации теоремы Шеннона) совпадает с длиной корреляции поля
) [59]. Максимальный шаг между отсчетами (в оптической интерпретации теоремы Шеннона) совпадает с длиной корреляции поля  в плоскости
в плоскости  . Добавим, что образ близкий к
. Добавим, что образ близкий к  , восстановится и в том случае, когда шаг между отсчетами не является постоянным, а случайным образом меняется. Однако средняя величина этого шага совпадает с
, восстановится и в том случае, когда шаг между отсчетами не является постоянным, а случайным образом меняется. Однако средняя величина этого шага совпадает с 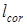 [59].
[59].
Допустим, что область, в которой  переносит большую часть энергии, содержит
переносит большую часть энергии, содержит  нулей амплитуды поля. Как известно [9; 12], среднее расстояние между нулями равно
нулей амплитуды поля. Как известно [9; 12], среднее расстояние между нулями равно 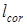 .
.
Рассмотрим в этой области некоторую выборку точечных источников с координатами  . При этом амплитуда и фаза этих источников
. При этом амплитуда и фаза этих источников  совпадает с амплитудой и фазой поля в точках
совпадает с амплитудой и фазой поля в точках  , а количество источников равняется количеству вихрей. Такую выборку будем называть «случайной» и она может быть описана соотношением
, а количество источников равняется количеству вихрей. Такую выборку будем называть «случайной» и она может быть описана соотношением
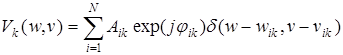 (2.25)
(2.25)
Учитывая тот факт, что среднее расстояние между отсчетами 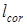 (их количество совпадает с количеством вихрей), выборка (2.25) должна восстановить поле, близкое к
(их количество совпадает с количеством вихрей), выборка (2.25) должна восстановить поле, близкое к  .
.
На рисунке 2.13 приведены результаты компьютерного восстановления «тест»-поля  . В качестве «тест»-поля использовалась совокупность случайно расположенных точечных источников единичной амплитуды, фаза которых случайна и меняется в пределах, значительно превышающих
. В качестве «тест»-поля использовалась совокупность случайно расположенных точечных источников единичной амплитуды, фаза которых случайна и меняется в пределах, значительно превышающих 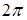 . Позиции источников были выбраны так, что размещение точечных источников напоминало три вертикальные полосы (рис. 2.13 а).
. Позиции источников были выбраны так, что размещение точечных источников напоминало три вертикальные полосы (рис. 2.13 а).

 Рис. 2.13 b соответствует восстановлению шенноновской выборкой. Рис. 2.13 c – результаты восстановления случайной выборкой.
Рис. 2.13 b соответствует восстановлению шенноновской выборкой. Рис. 2.13 c – результаты восстановления случайной выборкой.
Пространственный шаг между значениями выборки выбирался таким образом:
1. В случае шенноновской выборки расстояние между соседними отсчетами  не превышала длины корреляции поля
не превышала длины корреляции поля  , что отвечает условиям теоремы Котельникова – Шеннона [59]. Величина
, что отвечает условиям теоремы Котельникова – Шеннона [59]. Величина  , как обычно, определялась, исходя из поперечных размеров начального тест-поля.
, как обычно, определялась, исходя из поперечных размеров начального тест-поля.
2.  Для «случайной» выборки координаты отсчетов определялись как случайные. При этом среднее расстояние между отсчетами
Для «случайной» выборки координаты отсчетов определялись как случайные. При этом среднее расстояние между отсчетами  тоже равнялась
тоже равнялась  . Как показано в [59], в этом случае также возможна достаточно точная реконструкция начального поля.
. Как показано в [59], в этом случае также возможна достаточно точная реконструкция начального поля.
Сделаем следующее допущение. Пусть позиции точечных источников случайной выборки сдвинуты относительно позиций вихрей поля на величину 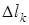 . Для определенности пусть направление сдвига совпадает с направлением оси
. Для определенности пусть направление сдвига совпадает с направлением оси 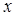 .
.
 Такую выборку будем называть «сдвинутой вихревой» выборкой. Из случайной природы поля
Такую выборку будем называть «сдвинутой вихревой» выборкой. Из случайной природы поля  следует, что и позиции вихрей
следует, что и позиции вихрей  поля будут случайными. Поэтому по структуре, статистическим параметрам такая выборка ничем не отличается от выборки (2.25). Следовательно, можно ожидать восстановления образа, аналогичного полю
поля будут случайными. Поэтому по структуре, статистическим параметрам такая выборка ничем не отличается от выборки (2.25). Следовательно, можно ожидать восстановления образа, аналогичного полю  , подобного образу, изображенному на рис. 2.13 c.
, подобного образу, изображенному на рис. 2.13 c.
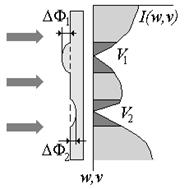
Однако это не совсем так [60]. Прежде всего, заметим, что сеть вихрей поля  как поля общего вида состоит из анизотропных вихрей. Однако, как показано в пункте 1.1, система таких вихрей может быть заменена с точностью до
как поля общего вида состоит из анизотропных вихрей. Однако, как показано в пункте 1.1, система таких вихрей может быть заменена с точностью до 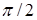 на систему изотропных. Такого типа замена аналогична ситуации, когда на пути пучка размещают прозрачную плоскопараллельную пластинку, которая в области малых амплитуд незначительно меняет толщину (рис. 2.14). Очевидно, что поле после такой пластики фактически не изменится, и после обратного Фурье-преобразования снова сформируется исходное изображение
на систему изотропных. Такого типа замена аналогична ситуации, когда на пути пучка размещают прозрачную плоскопараллельную пластинку, которая в области малых амплитуд незначительно меняет толщину (рис. 2.14). Очевидно, что поле после такой пластики фактически не изменится, и после обратного Фурье-преобразования снова сформируется исходное изображение  .
.
Допустим, что  – малая величина, и модуль амплитуды поля подчиняется линейному приближению в окрестности нулей.
– малая величина, и модуль амплитуды поля подчиняется линейному приближению в окрестности нулей.
В этом случае
 , (2.26)
, (2.26)
где  – амплитудный фактор, определяющий поведение модуля амплитуды (скорость «нарастания» поля) в окрестности i -го нуля в
– амплитудный фактор, определяющий поведение модуля амплитуды (скорость «нарастания» поля) в окрестности i -го нуля в  -направлении.
-направлении.
Поле, сформированное восстанавливающей выборкой в плоскости изображения, является Фурье-образом поля 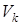 и описывается соотношением:
и описывается соотношением:
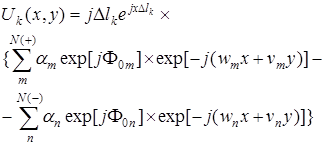 , (2.27)
, (2.27)
где  – координаты нулей;
– координаты нулей;  – количество положительных и отрицательных вихрей;
– количество положительных и отрицательных вихрей;  – начальная фаза i -го вихря.
– начальная фаза i -го вихря.
Как можно увидеть из (2.27),  с точностью до постоянного множителя
с точностью до постоянного множителя 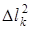 не зависит от
не зависит от  . Если
. Если  , то
, то  также можно считать независящей от
также можно считать независящей от  .
.
Заменим выборку (2.25) на следующую систему элементарных полей:
 , (2.28)
, (2.28)
где 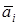 – усредненное в окрестности i -го вихря
– усредненное в окрестности i -го вихря 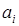 , а
, а  (в полярных координатах
(в полярных координатах 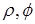 с началом в центре вихря) имеет вид
с началом в центре вихря) имеет вид
 , (2.29)
, (2.29)
где  – «вихревая» амплитудная функция, равная нулю при
– «вихревая» амплитудная функция, равная нулю при  .
.
В этом случае (2.27) трансформируется в соотношение
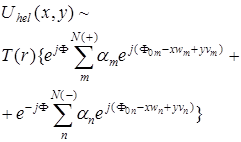 , (2.30)
, (2.30)
где  ,
,  ,
,  , и в области анализа стремятся к
, и в области анализа стремятся к 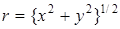 , если пространственные размеры
, если пространственные размеры  небольшие (см. Аппендикс 2). Заметим, что представление восстанавливающего поля в виде (2.25) можно интерпретировать как некоторую выборку из поля (2.27).
небольшие (см. Аппендикс 2). Заметим, что представление восстанавливающего поля в виде (2.25) можно интерпретировать как некоторую выборку из поля (2.27).
Таким образом, интенсивности восстановленных полей в обоих случаях будут промодулированы функцией, аналогом  . Особенностью такой «вихревой» модулирующей функции является равенство нулю в точке
. Особенностью такой «вихревой» модулирующей функции является равенство нулю в точке  и ее монотонное увеличение при отходе от этой точки.
и ее монотонное увеличение при отходе от этой точки.
Результаты компьютерного моделирования по восстановлению изображения сдвинутой выборкой представлены на рис. 2.15. Как видно из рисунков, восстановленное на основе сдвинутой выборки поле действительно промодулировано функцией типа  . Для подчеркивания радиальной симметрии модулирующей функции в восстановленное изображение вписано белое кольцо (рис. 2.15 c). Рис. b поясняет принципы формирования «сдвинутой» выборки. Сдвиг координат выборки осуществлялся как в направлении оси
. Для подчеркивания радиальной симметрии модулирующей функции в восстановленное изображение вписано белое кольцо (рис. 2.15 c). Рис. b поясняет принципы формирования «сдвинутой» выборки. Сдвиг координат выборки осуществлялся как в направлении оси  , так и в направлении оси
, так и в направлении оси  . Как видим из рисунка, практически до величин сдвига порядка 0.5
. Как видим из рисунка, практически до величин сдвига порядка 0.5  (рис. c – e) характер восстановленного поля не изменяется. Даже для
(рис. c – e) характер восстановленного поля не изменяется. Даже для 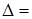 0.75
0.75  (рис. f) в центре изображения сохраняется темная область. Лишь для величин сдвига больше
(рис. f) в центре изображения сохраняется темная область. Лишь для величин сдвига больше  (рис. g, h) можно утверждать, что поле, реконструированное на основе сдвинутой выборки, стает подобным полю, восстановленному случайной выборкой, т.е. влияние вихрей на формирование структуры поля стает таким незначительным, что сдвинутая выборка превращается фактически в случайную.
(рис. g, h) можно утверждать, что поле, реконструированное на основе сдвинутой выборки, стает подобным полю, восстановленному случайной выборкой, т.е. влияние вихрей на формирование структуры поля стает таким незначительным, что сдвинутая выборка превращается фактически в случайную.
Иными словами, восстановленное поле «помнит», что оно сформировано точечными источниками, фаза которых определяется фазовым геликоидом вихревой структуры, если сдвиг восстанавливающей выборки не превышает величины порядка  .
.
Таким образом, проанализировав результаты восстановления
тест-полей на основе сдвинутых выборок можно, утверждать, что «фазовое» влияние отдельного вихря распространяется на расстояние, сравнимое с длиной корреляции поля.


2.7.2. Восстановление изображения регулярной выборкой, полученной на основе анализа параметров вихрей случайного поля
Как показано в [12], поле в Фурье-плоскости (дальней зоне) может быть представлено на основе так называемого произведения волновых функций:
 , (2.31)
, (2.31)
где 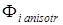 – изменение фазы в окрестности
– изменение фазы в окрестности  -го вихря.
-го вихря.
Если заменить систему анизотропных вихрей поля на систему изотропных, (2.31) может быть переписано в виде:
 , (2.32)
, (2.32)
где  – истинный модуль амплитуды;
– истинный модуль амплитуды;  ,
,  ; координаты
; координаты  связаны с центром
связаны с центром  -го вихря;
-го вихря;  – топологический заряд
– топологический заряд  -го изотропного вихря.
-го изотропного вихря.
Заметим, что исходя из выражения (2.32) и вследствие того, что результирующая фаза поля формируется как сумма элементарных фаз, которые ассоциируются с каждым вихрем, сумма начальных фаз изотропных вихрей:
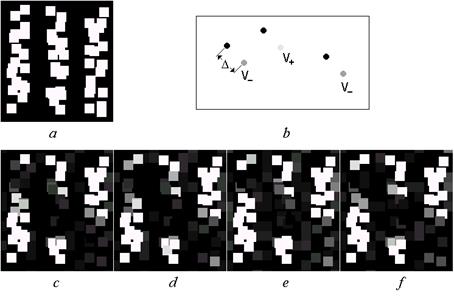
 (2.33)
(2.33)
 формирует лишь постоянный фазовый сдвиг, одинаковый для всего поля. В этом смысле, начальная фаза изотропного вихря не является актуальной при формировании структуры поля, чем можно пренебречь. Очевидно, что такой вывод приводит к абсолютно другому пониманию ситуации, которая складывается в поле при замене анизотропных вихрей на изотропные. Поле в границах каждого (произвольного) спекла формируется «одинаковыми» вихрями, отличающимися только знаком топологического заряда. Это, в свою очередь, приводит к тому, что восстановление поля на основе сдвинутых выборок также должно происходить по-другому. Действительно, даже при значительной величине сдвига выборки и при переходе соответствующего отсчета из одного спекла в другой эта точка поля попадает под «влияние» такого же вихря.
формирует лишь постоянный фазовый сдвиг, одинаковый для всего поля. В этом смысле, начальная фаза изотропного вихря не является актуальной при формировании структуры поля, чем можно пренебречь. Очевидно, что такой вывод приводит к абсолютно другому пониманию ситуации, которая складывается в поле при замене анизотропных вихрей на изотропные. Поле в границах каждого (произвольного) спекла формируется «одинаковыми» вихрями, отличающимися только знаком топологического заряда. Это, в свою очередь, приводит к тому, что восстановление поля на основе сдвинутых выборок также должно происходить по-другому. Действительно, даже при значительной величине сдвига выборки и при переходе соответствующего отсчета из одного спекла в другой эта точка поля попадает под «влияние» такого же вихря.
Этот вывод подтвержден результатами компьютерного моделирования (рис. 2.16). На этом рисунке приведены результаты восстановления поля сдвинутыми выборками при замене анизотропных вихрей поля в дальней зоне на систему изотропных. Как и в предыдущем случае, сдвиг координат выборки осуществлялся как в направлении оси  , так и в направлении оси
, так и в направлении оси  . Мы видем, что в отличие от результатов, представленных на рис. 2.15, темная область в центре изображения сохраняется даже для сдвига
. Мы видем, что в отличие от результатов, представленных на рис. 2.15, темная область в центре изображения сохраняется даже для сдвига 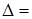 2
2  (рис. f).
(рис. f).
В заключение этого параграфа приведем результаты восстановления начального поля шенноновской выборкой, сформированной на основе характеристик системы изотропных вихрей. Принципы построения выборки следующие:
1. Шаг между отсчетами составляет величину порядка 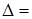 0.5
0.5 
2. Модуль амплитуды поля в точке отсчета совпадает с истинным значением, полученным как корень из интенсивности поля.
3. Фаза поля в точке  произвольного отсчета определяется соотношением:
произвольного отсчета определяется соотношением:
 , (2.34)
, (2.34)
где  – координаты ближайшего к точке
– координаты ближайшего к точке  изотропного вихря;
изотропного вихря; 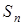 – его топологический заряд;
– его топологический заряд;  – начальная фаза этого вихря.
– начальная фаза этого вихря.
Фактически фаза в произвольной точке поля определяется как фаза ближайшего изотропного вихря, поскольку, как было показано выше, влияние вихря на формирование структуры поля распространяется, во всяком случае, на расстояние сравнимое с половиной длины корреляции поля. Так как шаг между отсчетами равняется 0.5  , то тем самым этот факт формально учитывается.
, то тем самым этот факт формально учитывается.
 Естественно, что такое утверждение выполняется лишь в статистическом смысле. Реально расстояние между нулями поля колеблется в широких пределах. Таким образом, в каждом конкретном случае влияние конкретного вихря распространяется на разное расстояние. Как показали проведенные оценки, фаза поля, реконструированная согласно соотношению (2.34), только в 75–80 % случаях совпадает с истинной фазой поля. За критерий «идентичности» фазы был выбранный критерий Релея. Считалось, что фаза, определенная по соотношению (2.34) совпадает с истинной фазой поля, если разница между ними не превышала
Естественно, что такое утверждение выполняется лишь в статистическом смысле. Реально расстояние между нулями поля колеблется в широких пределах. Таким образом, в каждом конкретном случае влияние конкретного вихря распространяется на разное расстояние. Как показали проведенные оценки, фаза поля, реконструированная согласно соотношению (2.34), только в 75–80 % случаях совпадает с истинной фазой поля. За критерий «идентичности» фазы был выбранный критерий Релея. Считалось, что фаза, определенная по соотношению (2.34) совпадает с истинной фазой поля, если разница между ними не превышала  .
.
 Добавим, что среднее отклонение рассчитанной фазы от истинной не превышало величины
Добавим, что среднее отклонение рассчитанной фазы от истинной не превышало величины  =
=  . Таким образом, в некоторых точках рассчитанная фаза совпадала с фазой поля практически полностью. Среднее отклонение
. Таким образом, в некоторых точках рассчитанная фаза совпадала с фазой поля практически полностью. Среднее отклонение  в точках, в которых разница между фазами была больше чем
в точках, в которых разница между фазами была больше чем  , не превышало величины
, не превышало величины  (20 – 25% точек).
(20 – 25% точек).
Результаты восстановления поля такой шенноновской выборкой представлены на рис. 2.17 b. Как видно из рисунка, реконструированное на основе регулярной выборки поле (с  , рассчитанной в соответствии с соотношением (2.36)) стремится к начальному изображению тест-объекта. Относительно темная зона в середине изображения может быть объяснена кооперативным воздействием (см. выше) системы изотропных вихрей.
, рассчитанной в соответствии с соотношением (2.36)) стремится к начальному изображению тест-объекта. Относительно темная зона в середине изображения может быть объяснена кооперативным воздействием (см. выше) системы изотропных вихрей.
Таким образом, полученные результаты позволяют сделать следующие выводы:
1. «Фазовое влияние» отдельного вихря распространяется на расстояние, сравнимое с длиной корреляции поля.
2. Восстановленное поле промодулировано «вихревой» амплитудной функцией, если реконструирующая выборка точечных источников по координатам совпадает со сдвинутой сетью нулей поля.
3. Сеть анизотропных вихрей случайного поля может быть заменена системой изотропных вихрей. При этом влияние такой системы изотропных вихрей, ее отдельных вихрей на формирование структуры поля распространяется значительно дальше, чем влияние аналогичной системы анизотропных вихрей и значительно превышает длину корреляции поля.
4. Фаза в произвольной точке поля может быть определена с высокой вероятностью и ошибкой не больше чем  на основе анализа характеристик системы изотропных вихрей.
на основе анализа характеристик системы изотропных вихрей.
2.8. Определение знаков вихрей случайного поля
Подытожим установленные факты.
1. Сетки интенсивности и фазы связаны (хотя бы в статистическом смысле).
2. Седловые точки интенсивности преимущественно находятся в областях поля, где фаза меняется достаточно быстро, т.е. плотность эквифазных линий поля наибольшая, и, как правило, два соседних вихря разного знака можно соединить линией тока градиента, которая проходит через седловую точку интенсивности.
3. В пределах фазового спекла фаза меняется в границах 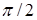 . Поэтому любая линия, которую можно провести в относительной близости от истинной эквифазовой линии, может быть с достаточно большой точностью принята за эту эквифазную линию.
. Поэтому любая линия, которую можно провести в относительной близости от истинной эквифазовой линии, может быть с достаточно большой точностью принята за эту эквифазную линию.
Тогда можно высказать следующую гипотезу «1»: линия тока градиента интенсивности, проходящая через седловую точку интенсивности, может быть отождествлена с одной из эквифазных линий поля фазы, соединяющей соседние вихри с различными знаками топологического заряда.
Иными словами, анализируя характеристики системы особых точек и линий тока градиента интенсивности, можно с точностью до знака присвоить топологические заряды вихрям поля и соединить их некоторыми эквифазными линиями. Результатом такого анализа может быть построение сети, которая близка к истинной сети вихрей, либо к аналогичной сети комплексно-сопряженного поля.
Естественно, что такое утверждение является справедливым лишь с определенной долей вероятности и, очевидно, выполняется не для всех участков поля. Однако правомерным является утверждение, что в поле могут быть выделены участки, для которых с точностью до знака топологического заряда вихрей может быть проведено такое соответствие.
Тогда логическим продолжением вышесказанного является следующая гипотеза «2»: поле может быть поделено на участки, для которых сеть, образованная абсолютными минимумами интенсивности и ее седловыми точками, соединенными линиями тока градиента, образует сеть, которая с точностью до знака топологического заряда достаточно близка к сети, образованной вихрями этого поля.
Отсюда следует, логический вывод, что если бы существовала возможность точного определения знака топологического заряда произвольного вихря поля, то знаки вихрей таких «элементарных» сетей могут быть однозначно согласованы и построена сеть, соответствующая истинной сети вихрей (возможно за небольшим исключением) для всего поля.
Очевидно, что построение такой сети эквивалентно решению обратной задачи – восстановлению фазы.
Как известно (см. п. 1.3), информацию о знаках вихрей можно получить из анализа результатов интерференционного эксперимента, поскольку вихревые структуры образуют вилочки при их интерференции с регулярной опорной волной.
Однако в большинстве случаев создание опорного пучка является проблематичным вследствие того, что предыстория анализируемого поля неизвестна.
Таким образом, возникает необходимость разработки метода, позволяющего получить информацию о знаках любого из вихрей анализируемого поля, распределение интенсивности которого известно.
При этом:
1. В общем случае поле – случайное.
2. Регулярная опорная волна не может быть сформирована.
3. Вывод о знаке вихря должен базироваться на данных интерферометрического эксперимента, поскольку только такого типа фазометрия дает однозначный ответ о знаке топологического заряда вихря.
Перед формулировкой основной идеи метода напомним некоторые факты, касающиеся характеристик случайного поля:
1. В центре спекла фаза практически постоянна, поскольку именно там расположены ее седловые точки.
2. Средние размеры спекла определяются длиной корреляции поля.
3. Любое поле является когерентным по отношению к самому себе.
В основу предлагаемого метода положено следующее.
Очевидно, что с помощью разделения анализируемого поля на две идентичные составляющие достаточно просто можно организовать интерференцию любого поля самого с собою. При этом можно контролировать такие параметры:
· Угол схождения между интерферирующими полями.
· Взаимный пространственный сдвиг между ними.
· Соотношение средних интенсивностей интерферирующих полей.
Пусть с помощью светоделителя поле 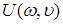 разделено на идентичные по структуре составляющие
разделено на идентичные по структуре составляющие  и
и 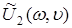 . При этом поле
. При этом поле 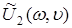 сдвинуто относительно поля
сдвинуто относительно поля  в плоскости
в плоскости  в произвольном направлении на величину
в произвольном направлении на величину  . Направления преимущественного распространения полей различны и такие, что поля описываются соотношениями:
. Направления преимущественного распространения полей различны и такие, что поля описываются соотношениями:
 (2.35)
(2.35)
где 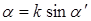 ;
;  ;
;  , а
, а 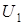 и
и  являются «точными копиями» поля
являются «точными копиями» поля  с соответствующими амплитудными коэффициентами, устанавливающими соотношение между средними интенсивностями этих полей.
с соответствующими амплитудными коэффициентами, устанавливающими соотношение между средними интенсивностями этих полей.
Тогда интенсивность суперпозиции этих полей опишется виражением:
 , (2.36)
, (2.36)
где  (
( ) – действительные и мнимые части комплексных амплитуд
) – действительные и мнимые части комплексных амплитуд 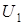 и
и  .
.
Отметим следующее:
1. Из (2.36) следует, что при величине  третье слагаемое равно нулю. Соответственно результирующая интерференционная картина представляет собой систему прямых интерференционных полос, промодулированных интенсивностью поля
третье слагаемое равно нулю. Соответственно результирующая интерференционная картина представляет собой систему прямых интерференционных полос, промодулированных интенсивностью поля 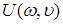 . Поле интерферирует с таким же полем и в любой его точке (несмотря на его сложную фазовую структуру) разность фаз между полями
. Поле интерферирует с таким же полем и в любой его точке (несмотря на его сложную фазовую структуру) разность фаз между полями 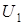 и
и  равна нулю.
равна нулю.
2. Взаимный сдвиг полей  и
и 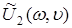 приводит к тому, что при определенной величине
приводит к тому, что при определенной величине  (меньше
(меньше  и больше
и больше  ) участки полей с вихрями интерферируют с практически плоскими волнами, которые соответствуют частям полей, локализованных в областях седловых точек фазы. Таким образом, при отличном от нуля
) участки полей с вихрями интерферируют с практически плоскими волнами, которые соответствуют частям полей, локализованных в областях седловых точек фазы. Таким образом, при отличном от нуля  , в местах локализации вихрей полей
, в местах локализации вихрей полей 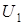 и
и  должны наблюдаться классические интерференционные вилочки.
должны наблюдаться классические интерференционные вилочки.
Дата добавления: 2015-07-12; просмотров: 159 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Фазовые вихри. | | | Сети вихрей – скелетон фазы скалярного поля 2 страница |