
|
Читайте также: |
При этом:
· вихри разных знаков, принадлежащие одному из полей (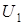 или
или  ), будут формировать разнонаправленные интерференционные вилочки.
), будут формировать разнонаправленные интерференционные вилочки.
· Направление вилочек также разное, если вихри одного знака принадлежат разным полям.
3. Как известно, максимальная видность интерференционной картины достигается при равной интенсивности интерферирующих пучков. При интерференции случайных полей однородная видность интерференционной картины невозможна, за исключением случая, когда сдвиг  . Однако вихри поля размещаются в зонах поля с малой интенсивностью. Соответственно при значительных сдвигах между полями
. Однако вихри поля размещаются в зонах поля с малой интенсивностью. Соответственно при значительных сдвигах между полями  максимальная видность интерференционной картины в зоне вихрей будет достигаться в случае, когда интенсивность одного из полей значительно превышает интенсивность другого.
максимальная видность интерференционной картины в зоне вихрей будет достигаться в случае, когда интенсивность одного из полей значительно превышает интенсивность другого.
Пусть средняя интенсивность несдвинутого поля 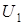 значительно выше, чем интенсивность поля
значительно выше, чем интенсивность поля  . Тогда максимально выгодные условия для интерференции будут возникать как раз для участков поля
. Тогда максимально выгодные условия для интерференции будут возникать как раз для участков поля 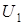 , в которых интенсивность поля минимальна, т.е. для участков поля с вихрями. В то же время для участков поля
, в которых интенсивность поля минимальна, т.е. для участков поля с вихрями. В то же время для участков поля  , которые содержат вихри, наоборот, условия интерференци будут наихудшими даже по сравнению с другими областями этого поля.
, которые содержат вихри, наоборот, условия интерференци будут наихудшими даже по сравнению с другими областями этого поля.
Иначе говоря, можно утверждать, что при определенном выборе соотношения интенсивностей сдвинутого и несдвинутого полей ( ) в интерференционной картине уверенно будут наблюдаться только вилочки, соответствующие несдвинутому полю.
) в интерференционной картине уверенно будут наблюдаться только вилочки, соответствующие несдвинутому полю.
Таким образом, отслеживая появление вилочек в суммарной интерференционной картине, их движение при увеличении  и регулируя соотношение интенсивностей интерферирующих полей, можно однозначно установить позиции и знаки вихрей поля.
и регулируя соотношение интенсивностей интерферирующих полей, можно однозначно установить позиции и знаки вихрей поля.
2.8.1. Результаты компьютерного моделирования «сдвиговой» интерференции спекл-полей
Проведенное рассмотрение было подтверждено данными компьютерного моделирования.
Результаты компьютерного моделирования приведены на рисунках 2.18 – 2.21.
Рисунок 2.18 иллюстрирует поведение интенсивности участка спекл-поля и соответствующую фазовую карту для различных величин сдвига  . Как видно из рисунка, для величины
. Как видно из рисунка, для величины  (рис. а) интерференционные полосы действительно прямые, характерных для вихрей вилочек не наблюдается. При наличии ненулевого сдвига, в местах поля, соответствующих локализации вихрей полей
(рис. а) интерференционные полосы действительно прямые, характерных для вихрей вилочек не наблюдается. При наличии ненулевого сдвига, в местах поля, соответствующих локализации вихрей полей 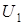 и
и  , появляются пары разнонаправленных вилочек (рис. b – d), возникающие в результате интерференции вихревых структур полей
, появляются пары разнонаправленных вилочек (рис. b – d), возникающие в результате интерференции вихревых структур полей 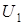 ,
,  и гладкими участками этих полей. По мере увеличения
и гладкими участками этих полей. По мере увеличения  вилочки, ассоциируемые с полем
вилочки, ассоциируемые с полем  , сдвигаются относи-тельно неподвижных вилочек, созданных полем
, сдвигаются относи-тельно неподвижных вилочек, созданных полем 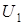 .
.

 На рис. 2.19 приведены расчетные интерферограммы сдви-га поля для различных величин сдвига парциальных полей.
На рис. 2.19 приведены расчетные интерферограммы сдви-га поля для различных величин сдвига парциальных полей.

Рис. 2.19
Интерферограммы сдвига поля для различных величин сдвига  .
.
a –  , b –
, b – 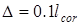 , c –
, c –  , d –
, d –  .
.

a b c
Рис. 2.20
Интерферограммы сдвига поля для различных взаимных угловых ориентаций полей 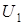 и
и  и величины сдвига
и величины сдвига  . Белыми стрелочками на рисунке а указаны позиции вихрей несдвинутого поля.
. Белыми стрелочками на рисунке а указаны позиции вихрей несдвинутого поля.

Рис. 2.21
Интерферограммы сдвига поля для величины сдвига  и различных соотношений интенсивностей полей
и различных соотношений интенсивностей полей 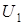 и
и  . Белыми стрелочками на рисунке а указаны позиции вихрей несдвинутого поля. a – средняя интенсивность поля
. Белыми стрелочками на рисунке а указаны позиции вихрей несдвинутого поля. a – средняя интенсивность поля 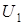 равна интенсивности поля
равна интенсивности поля  ; b – больше в 4 раза; c – больше в 16 раз; d – больше в 100 раз.
; b – больше в 4 раза; c – больше в 16 раз; d – больше в 100 раз.
Рис. 2.20 иллюстрирует результаты интерференции при различных взаимных угловых ориентациях полей 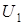 и
и  . Как следует из рисунка, для всех ориентаций вилочки, созданные идентичными вихрями полей
. Как следует из рисунка, для всех ориентаций вилочки, созданные идентичными вихрями полей 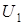 и
и  , разнонаправлены. При этом они как будто вложены одна в другую для ориентации, когда направление сдвига полей совпадает с направлением интерференционных полос.
, разнонаправлены. При этом они как будто вложены одна в другую для ориентации, когда направление сдвига полей совпадает с направлением интерференционных полос.
Рис. 2.21 иллюстрирует результаты интерференции при различных соотношениях интенсивностей полей 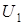 и
и  . Как следует из рисунков 2.21 c, d, начиная с величин превышения интенсивности поля
. Как следует из рисунков 2.21 c, d, начиная с величин превышения интенсивности поля 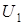 над полем
над полем  порядка 20 раз, в интерференционной картине практически наблюдаются только вилочки, созданные несдвинутым полем
порядка 20 раз, в интерференционной картине практически наблюдаются только вилочки, созданные несдвинутым полем 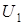 .
.
В заключение отметим, что проведенный анализ и полученные результаты позволяют по-новому взглянуть на физические основы существующих методов восстановления фазы поля по распределению его интенсивности и перейти к разработке принципиально новых алгоритмов решения подобных обратных задач [61 – 63].
2.8.2. Экспериментальное определение знаков нулей спекл-поля на основе анализа интерферограмм сдвига
Для подтверждения результатов теоретического рассмотрения метод нахождения характеристик вихрей с помощью сдвиговой интерферометрии был реализован в следующей схеме (см. рис. 2.22 a).

 Неколлимированный пучок от Не-Ne лазера освещал рассеивающий объект 1 (рис. 2.22 b), изготовленный из матового стекла. Величина дисперсии фазы граничного поля была выбрана таким образом, что регулярная составляющая пучка после объекта отсутствовала. На фокусном расстоянии от объекта устанавливался Фурье-преобразующий объектив 2, за которым располагался интерферометр 3 – 6. Одно из зеркал 4 и выходной светоделитель 6 устанавливались на прецизионных механических столиках, обеспечивающих возможность регулировки углов схождения и величин сдвига элементарных полей. За интерферометром в фокусе объектива устанавливалась CCD-камера, фиксировавшая результат интерференции.
Неколлимированный пучок от Не-Ne лазера освещал рассеивающий объект 1 (рис. 2.22 b), изготовленный из матового стекла. Величина дисперсии фазы граничного поля была выбрана таким образом, что регулярная составляющая пучка после объекта отсутствовала. На фокусном расстоянии от объекта устанавливался Фурье-преобразующий объектив 2, за которым располагался интерферометр 3 – 6. Одно из зеркал 4 и выходной светоделитель 6 устанавливались на прецизионных механических столиках, обеспечивающих возможность регулировки углов схождения и величин сдвига элементарных полей. За интерферометром в фокусе объектива устанавливалась CCD-камера, фиксировавшая результат интерференции.
 Результаты интерференции представлены на рисунке 2.23. Рисунок a соответствует нулевому сдвигу элементарных полей, рисунок b – сдвиг между полями порядка половины длины корреляции (среднего размера спекла).
Результаты интерференции представлены на рисунке 2.23. Рисунок a соответствует нулевому сдвигу элементарных полей, рисунок b – сдвиг между полями порядка половины длины корреляции (среднего размера спекла).
 Как видно из рисунка 2.23 b, вихри случайного поля достаточно уверенно идентифицируются.
Как видно из рисунка 2.23 b, вихри случайного поля достаточно уверенно идентифицируются.
3.Сингулярности векторного поля
В векторном электромагнитном поле, характеристики которого в общем случае пространственно распределены, можно, как и для скалярного поля, выделить определенные множества особых точек, объединенных в особые сети. Очевидно, можно рассчитывать на то, что, как и в скалярном случае, благодаря свойствам Эвклидова пространства, характеристики таких сетей должны дать исследователю информацию (хотя бы на качественном уровне) о поведении поля в любой его точке. Иными словами, можно ожидать, что и для векторного поля возможно построение его топологического скелетона, характеристики которого определяют закономерности изменения характеристик поля от точки к точке.
Однако ситуация в векторном монохроматическом поле кардинально отличается от ситуации в скалярном: в векторном поле отсутствуют стационарные нули интенсивности [3; 68 – 71]. Действительно, для существования стационарного нуля векторного поля требуется одновременное существование в одной точке нулей всех трех ортогональных компонент. Вероятность такого события нулевая. Более того, существование такого нуля проблематично, даже если допустить возможность его возникновения, поскольку как угодно малое возмущение поля приведет к немедленному смещению нулей компонент относительно их первоначальных позиций.
Поэтому о стационарном дефекте такого типа можно говорить только с точки зрения модельных представлений, когда реальное расстояние между нулями компонент невелико, и разницу в их локализации невозможно определить с помощью экспериментальных средств исследования поля [68 – 71]. В этом случае поле в окрестности «модельного» дефекта будет вести себя так же, как и в случае реального нуля векторного поля.
3.1. Реализация сингулярных моделей
Остановимся еще на одном вопросе, который, с нашей точки зрения имеет принципиальный характер. Утверждается, что для анализа векторных, однородно поляризованных полей могут быть использованы скалярные подходы (см., например, [8]). Однако это не совсем так.
Покажем, что даже в случае однородно поляризованных полей, т.е. в случае так называемых скалярных оптических полей, абсолютных нулей амплитуды не существует, и определим пределы, в которых эти понятия можно применять для описания оптических явлений.
3.1.1. «Абсолютные» («стационарные») нули интенсивности в оптическом поле
Известно, что скалярное описание поля, как утверждается в [8], справедливо только для поляризационно-однородных полей. Требование пространственной поляризационной однородности выполняется для случая рассеивающего объекта, не меняющего поляризацию освещающего пучка, и одновременном выполнении параксиального приближения. Авторы допускают, что вкладом продольной ( -вой) компоненты поля
-вой) компоненты поля  в амплитуду и интенсивность поля можно пренебречь в связи с ее малостью [8].
в амплитуду и интенсивность поля можно пренебречь в связи с ее малостью [8].
Однако такое утверждение является справедливым для любой области поля, кроме зон, где интенсивность поля мала. Действительно, именно в регионах поля, где поперечные компоненты  стремятся к нулю, продольная компонента
стремятся к нулю, продольная компонента  становится сравнимой с ними по величине. Иначе говоря, в «однородно» поляризованных полях, в областях с малой интенсивностью, при описании поведения поля необходимо учитывать все три компоненты. Далее покажем, что поле в таких зонах поляризационно неоднородно, а его амплитуда не достигает значения абсолютного нуля.
становится сравнимой с ними по величине. Иначе говоря, в «однородно» поляризованных полях, в областях с малой интенсивностью, при описании поведения поля необходимо учитывать все три компоненты. Далее покажем, что поле в таких зонах поляризационно неоднородно, а его амплитуда не достигает значения абсолютного нуля.
Традиционный анализ поля осуществляется по следующей схеме [5; 8]:
1. Априорно допускается, что в некоторой окрестности поля существует нуль амплитуды.
2. В области (окрестности) нуля рассматриваются решения общего уравнения поля (уравнения Максвелла, параболического уравнения и т.д.).
3. Рассматривается траектория нулевого значения амплитуды поля в пространстве.
Естественно, что такой подход имеет право на существование, и, как известно, он оказался достаточно плодотворным. Однако, несмотря на это, для традиционного подхода можно выделить ряд недостатков:
1. Прежде всего, предположение о существовании в некоторых точках поля абсолютного нуля амплитуды не является очевидным (все три компоненты  и
и  равны нулю), поскольку базируется на предположении равенства нулю не только поперечных компонент но, и
равны нулю), поскольку базируется на предположении равенства нулю не только поперечных компонент но, и  -вой компоненты поля.
-вой компоненты поля.
2. Анализ поля в терминах решений общих уравнений (именно из-за его общности) не позволяет, как правило, проследить связи характеристик поля с параметрами рассеивающего объекта, с геометрией анализа поля, определяемой, прежде всего, расстоянием от рассеивателя до плоскости анализа).
Учитывая недостатки традиционного подхода и для соответствия рассчетов реальным физическим объектам, мы предлагаем подход, который сохраняет основные достоинства общего подхода, однако позволяет значительно упростить рассмотрение:
1. Рассеивающий объект предполагается достаточно тонким и плоским.
2. При когерентном облучении объекта из фундаментальных представлений о рассеянном поле следует существование корреляционной структурности граничного поля – поля непосредственно за объектом [40]. Такой подход позволяет представить граничное поле набором некоторых зон корреляции, характеристики которых зависят от характеристик самого рассеивающего объекта и расстояния от объекта до плоскости анализа. Совокупность таких зон корреляции можно интерпретировать как набор элементарных излучателей, обладающих определенными параметрами.
Так, например, на достаточно большом расстоянии от объекта граничное поле может быть представлено ансамблем точечных источников, а в зоне неразвитой спекл-структуры (волновой зоне) – зоне рождения нулей, поле непосредственно за объектом может быть представлено совокупностью элементарных волн с простыми волновыми поверхностями.
3. Далее в зоне анализа аналитически рассчитывается поле, формируемое отдельно выделенными зонами корреляции граничного поля.
4. И, наконец, в произвольной точке плоскости анализа рассчитывается и анализируется поле в допущении, что хотя бы одна из компонент поля равна нулю. Последнее утверждение не противоречит вышесказанному о существовании нулей поля, поскольку для отдельной компоненты полностью справедливый скалярный подход.
Будем рассматривать поле в зоне, для которой парциальные волны, отвечающие зонам корреляции граничного поля, могут быть представлены сферическими волнами. Тогда совокупность зон корреляции поля непосредственно за объектом можно интерпретировать как набор точечных источников.
Условно разделим рассеивающие объекты на два класса. К первому классу отнесем объекты, для которых поляризационные характеристики граничного поля такие же, как и для облучающего пучка (объекты типа фазового экрана) [40]. Модуляция поля непосредственно за объектом – чисто фазовая.
Второй класс объектов – объекты, для которых уже в граничном поле наблюдается поляризационная неоднородность (например, объекты, для которых реализуется многократное рассеивание).
Пусть плоский и тонкий рассеивающий объект (см. рис. 3.1) нормально облучается плоской волной с произвольной поляризацией. Поле непосредственно за объектом представим набором комплексных амплитуд точечных источников:
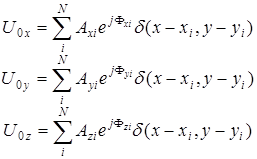 , (3.1)
, (3.1)
где 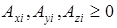 – модули амплитуды компонент;
– модули амплитуды компонент;  – фазы точечных источников;
– фазы точечных источников; 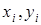 – координаты источников излучения.
– координаты источников излучения.
Для объектов первого класса  , где
, где  – положительные коэффициенты, а
– положительные коэффициенты, а 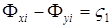 ,
, 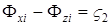 – разности фаз компонент. Заметим, что
– разности фаз компонент. Заметим, что  и
и  одинаковые для всех источников. Для объектов второго класса
одинаковые для всех источников. Для объектов второго класса 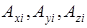 ,
,  – случайные величины. Поскольку анализ поля проводится в зоне, где излучение элементарного излучателя представляется сферической
– случайные величины. Поскольку анализ поля проводится в зоне, где излучение элементарного излучателя представляется сферической

 волной, то вклад компоненты
волной, то вклад компоненты  невелик и им можно пренебречь. Тогда, из простых геометрических соображений вытекает, что в любой точке наблюдения
невелик и им можно пренебречь. Тогда, из простых геометрических соображений вытекает, что в любой точке наблюдения  на расстоянии
на расстоянии  от объекта, компоненты поля каждого источника
от объекта, компоненты поля каждого источника  и
и  будут вносить свой вклад во все три компоненты анализируемого поля.
будут вносить свой вклад во все три компоненты анализируемого поля.
Поле, сформированное 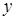 -компонентой
-компонентой  -того источника, запишется в виде:
-того источника, запишется в виде:
 , (3.2)
, (3.2)
где 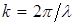 ;
; 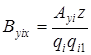 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Аналогично запишется выражение для 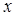 -компоненты поля путем замены индексов, соответствующих
-компоненты поля путем замены индексов, соответствующих 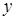 -компоненте на индексы
-компоненте на индексы 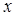 -компоненты:
-компоненты:
 , (3.3)
, (3.3)
где  ;
;  ;
; 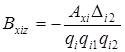 .
.
Результирующее поле, сформированное обоими компонентами поля  -того точечного источника, определяется как сумма
-того точечного источника, определяется как сумма 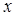 - и
- и 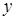 -компонент:
-компонент:
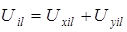 , (3.4)
, (3.4)
где индекс  соответствует координатам
соответствует координатам  .
.
Необходимо отметить, что, рассматривая только две компоненты поля, излучаемые парциальными источниками, мы учитываем образование  -компоненты в плоскости анализа как результат геометрии распространения волны.
-компоненты в плоскости анализа как результат геометрии распространения волны.
Результирующее поле, сформированное всеми элементарными источниками в точке  плоскости анализа, определяется суммой парциальных полей:
плоскости анализа, определяется суммой парциальных полей:
 . (3.5)
. (3.5)
Разложим в ряд Тейлора каждую из компонент поля в окрестности точки наблюдения. При этом считаем, что окрестность небольшая, и в ее границах изменением амплитуды элементарной волны будем пренебрегать, считая ее в окрестности точки  постоянной.
постоянной.
В этом случае можно ограничиться нулевым и линейным членами разложения
 . (3.6)
. (3.6)
Коэффициенты разложения запишутся в виде
 (3.7)
(3.7)
Поле компонент в окрестности точки наблюдения будет описываться выражением
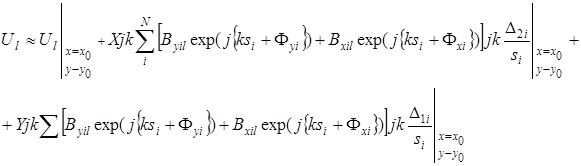 ,(3.8)
,(3.8)
где 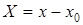 ,
, 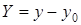 .
.
Введем Декартову и полярную системы координат, связанные с точкой наблюдения, для которых соответственно  ,
, 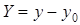 ,
,  ,
,  . Направление оси
. Направление оси  оставим без изменений, а угол
оставим без изменений, а угол  будем отсчитывать от оси
будем отсчитывать от оси  . Выделим из экспоненциальной формы записи комплексной амплитуды поля действительную и мнимую части.
. Выделим из экспоненциальной формы записи комплексной амплитуды поля действительную и мнимую части.
Тогда отдельные компоненты поля описываются соотношениями:
 (3.9)
(3.9)
Таким образом, выражение для компонент поля можно записать в виде:
 , (3.10)
, (3.10)
где  ;
; 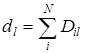 ;
;  ;
;  ;
;  ;
; 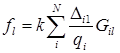 ;
;  ;
;  ;
;  ;
; 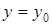 .
.
Проанализируем соотношение (3.10). Среднее значение  зависит от характеристик поля непосредственно за рассеивающим объектом. Его величина зависит как от характеристик облучающего объект пучка, так и от самого рассеивающего объекта. Иначе говоря,
зависит от характеристик поля непосредственно за рассеивающим объектом. Его величина зависит как от характеристик облучающего объект пучка, так и от самого рассеивающего объекта. Иначе говоря,  определяется функциями распределения величин
определяется функциями распределения величин  . Скорость изменения значения
. Скорость изменения значения  вдоль оси
вдоль оси  (
( ) не зависит от поляризационных характеристик точечных источников, если
) не зависит от поляризационных характеристик точечных источников, если 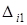 и
и  изменяются в одинаковых пределах. Как справедливо отмечено в [5; 8], для объектов первого типа и линейно поляризованного облучающего пучка (для определенности пусть вектор напряженности волны колеблется вдоль оси
изменяются в одинаковых пределах. Как справедливо отмечено в [5; 8], для объектов первого типа и линейно поляризованного облучающего пучка (для определенности пусть вектор напряженности волны колеблется вдоль оси  )
)  и
и  намного меньше, чем
намного меньше, чем  . Вместе с тем, из соотношения (3.7) следует, что коэффициенты при
. Вместе с тем, из соотношения (3.7) следует, что коэффициенты при  ,
,  и нулевые члены – случайные независимые величины.
и нулевые члены – случайные независимые величины.
Продемонстрируем это для нулевых членов для объектов, не меняющих поляризации. Пусть при этом поляризация облучающего пучка линейная, а вектор напряженности электрического поля параллельный оси  . В этом случае коэффициенты
. В этом случае коэффициенты  и соответственно
и соответственно
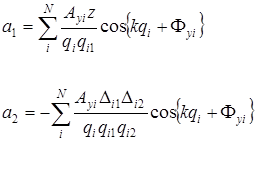 , (3.8)
, (3.8)
а коэффициент корреляции двух величин 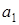 и
и  , по определению [2] равен
, по определению [2] равен
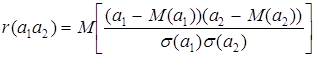 . (3.9)
. (3.9)
Легко видеть, что  и
и  равны нулю. Тогда радиус корреляции для коэффициентов
равны нулю. Тогда радиус корреляции для коэффициентов 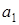 и
и  запишется в виде
запишется в виде
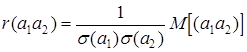 . (3.10)
. (3.10)
Если 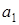 и
и  – независимые случайные величины, то
– независимые случайные величины, то 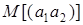 должно равняться нулю. Это непосредственно следует из того факта, что
должно равняться нулю. Это непосредственно следует из того факта, что 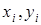 – независимые равномерно распределенные величины. Аналогично можно показать, что независимо от типа рассеивающего объекта все остальные коэффициенты разложения поля в (3.7) независимые случайные величины. Необходимо отметить, что при освещении объекта типа фазовый экран эллиптически поляризованным светом коэффициенты разложения, отвечающие координатам
– независимые равномерно распределенные величины. Аналогично можно показать, что независимо от типа рассеивающего объекта все остальные коэффициенты разложения поля в (3.7) независимые случайные величины. Необходимо отметить, что при освещении объекта типа фазовый экран эллиптически поляризованным светом коэффициенты разложения, отвечающие координатам 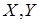 , не являются статистически независимыми. Так, например, при освещении такого объекта циркулярно поляризованным светом коэффициенты разложения при
, не являются статистически независимыми. Так, например, при освещении такого объекта циркулярно поляризованным светом коэффициенты разложения при 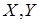 равны. В тоже время эти коэффициенты статистически независимы по сравнению с коэффициентами при
равны. В тоже время эти коэффициенты статистически независимы по сравнению с коэффициентами при  .
.
Дата добавления: 2015-07-12; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сети вихрей – скелетон фазы скалярного поля 1 страница | | | Сети вихрей – скелетон фазы скалярного поля 3 страница |