
|
Читайте также: |
Из (4.19) видно, что при совпадении знаков 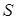 и
и 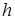 модуль поперечной компоненты вектора Умова – Пойнтинга тождественно равен нулю (
модуль поперечной компоненты вектора Умова – Пойнтинга тождественно равен нулю ( ) во всей анализируемой области. Физически это означает, что момент импульса поля в области такой
) во всей анализируемой области. Физически это означает, что момент импульса поля в области такой  -точки также равен нулю. Иными словами, орбитальный момент компенсируется спиновым.
-точки также равен нулю. Иными словами, орбитальный момент компенсируется спиновым.
Поэтому дальше будем предполагать, что 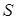 и
и  разных знаков:
разных знаков:
 . (4.20)
. (4.20)
В этом случае модуль поперечной составляющей ведет себя аналогично своей продольной составляющей и совершает «ротацию» во времени вокруг  -точки с двойной частотой светового колебания [107; 108]. Направление ротации минимума (максимума) определяется лишь знаком топологического заряда вибрационной фазы. Минимум
-точки с двойной частотой светового колебания [107; 108]. Направление ротации минимума (максимума) определяется лишь знаком топологического заряда вибрационной фазы. Минимум  достигается на
достигается на  -контуре и соответствует положению наевской дисклинации. Для заданного распределения комплексных амплитуд (4.11), (4.12)
-контуре и соответствует положению наевской дисклинации. Для заданного распределения комплексных амплитуд (4.11), (4.12)  -контур – окружность.
-контур – окружность.  -точка расположена в ее центре.
-точка расположена в ее центре.
Рис. 4.15 иллюстрирует поведение модуля поперечной составляющей во времени.
Естественно, что при более сложной структуре интерферирующих пучков поля в окрестности  -точки (векторное поле в окрестности не может быть рассмотрено как суперпозиция изотропного вихря и плоской волны) и соотношение (4.19) не имеет места. Однако характер изменений
-точки (векторное поле в окрестности не может быть рассмотрено как суперпозиция изотропного вихря и плоской волны) и соотношение (4.19) не имеет места. Однако характер изменений  тот же.
тот же.

Рис. 4.15
Ротация минимума поперечной составляющей вектора Умова – Пойнтинга (дисклинации) вокруг  -точки. Положение дисклинации на
-точки. Положение дисклинации на  -контуре отмечено белой точкой.
-контуре отмечено белой точкой.
b. Момент импульса поля в окрестности С-точки.
В соответствии с определением, плотность момента импульса описывается соотношением:
 . (4.21)
. (4.21)
Тогда, учитывая (4.18), имеем:
 . (4.22)
. (4.22)
Усредненный по времени (по одному периоду колебаний волны  ) момент импульса поля в области
) момент импульса поля в области  имеет вид
имеет вид
 . (4.23)
. (4.23)
В конечном итоге имеем [108-110]:
 , (4.24)
, (4.24)
где  – мощность вихревого пучка.
– мощность вихревого пучка.
Чтобы сравнить полученное выражение с моментом вихря ( [84]), напомним, что мощность циркулярно поляризованного вихря как пучка, формирующего поляризационно неоднородную ячейку с
[84]), напомним, что мощность циркулярно поляризованного вихря как пучка, формирующего поляризационно неоднородную ячейку с  -точкой, в два раза больше, чем
-точкой, в два раза больше, чем  . Учитывая это, для нормированных мощностей имеем соотношение:
. Учитывая это, для нормированных мощностей имеем соотношение:
 . (4.25)
. (4.25)
Таким образом, момент импульса в окрестности  -точки в два раза больше чем у вихревого пучка, если
-точки в два раза больше чем у вихревого пучка, если  и
и 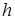 разного знака (спиновый и орбитальный моменты поля взаимно усиливают друг друга) и равен нулю, если знаки совпадают (спиновый и орбитальный моменты поля взаимно компенсируют друг друга).
разного знака (спиновый и орбитальный моменты поля взаимно усиливают друг друга) и равен нулю, если знаки совпадают (спиновый и орбитальный моменты поля взаимно компенсируют друг друга).

a b c d
Рис. 4.16
Временное поведение поперечной компоненты вектора Умова – Пойнтига в окрестности  -точки при несовпадении знаков топологического заряда и handedness фактора. Азимут компоненты соответствует ориентации стрелочек. Длина стрелки соответствует величине модуля компоненты.
-точки при несовпадении знаков топологического заряда и handedness фактора. Азимут компоненты соответствует ориентации стрелочек. Длина стрелки соответствует величине модуля компоненты.
Рисунок 4.16 иллюстрирует распределение не только модуля, но и азимута мгновенной поперечной компоненты вектора Пойнтинга. Азимут компоненты соответствует ориентации стрелочек, а величина ее модуля характеризуется длиной стрелки.
Из рисунка следует, что соответствующая дисклинации, мгновенная сингулярность поперечной компоненты вектора Умова – Пойнтинга является дефектом вихревого типа с положительной хиральностью (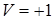 , направление прецессии вектора совпадает с направлением движения часовой стрелки).
, направление прецессии вектора совпадает с направлением движения часовой стрелки).



Рассмотрим поведение поперечной компоненты в различных точках линии, пересекающей область с неоднородной поляризацией и проходящей через  -точку (положение линии совпадает с одним из диаметров
-точку (положение линии совпадает с одним из диаметров  -контура) для различных моментов времени (рис. 4.17). Как видим, лишь для точки поля, совпадающей с положением
-контура) для различных моментов времени (рис. 4.17). Как видим, лишь для точки поля, совпадающей с положением  -точки, усредненная поперечная компонента вектора Умова – Пойнтинга будет иметь нулевое значение и ее величина будет нарастать по мере удаления от
-точки, усредненная поперечная компонента вектора Умова – Пойнтинга будет иметь нулевое значение и ее величина будет нарастать по мере удаления от  -точки.
-точки.
Поведение усредненной поперечной компоненты вектора Умова – Пойнтинга представлено на рис. 4.18. Как следует из рисунка, распределение модуля и азимута поперечной компоненты вектора Умова – Пойнтинга подобно такому же распределению, свойственному обычному вихрю. Однако в случае скалярного вихря все три компоненты вектора равны нулю, тогда как в нашем случае  -компонента ненулевая. Таким образом, поток энергии в центре линейно или циркулярно поляризованного вихря отсутствует и, как правило, является максимальным в
-компонента ненулевая. Таким образом, поток энергии в центре линейно или циркулярно поляризованного вихря отсутствует и, как правило, является максимальным в  -точке. При этом направление распространения энергии совпадает с направлением оси
-точке. При этом направление распространения энергии совпадает с направлением оси  .
.
c. Элементарные поляризационные ячейки с двумя  -точками одного знака
-точками одного знака
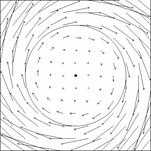
 Фазовая карта циркулярно поляризованного пучка с двумя вихрями одного знака представлена на рис. 4.19. На этом же рисунке приведено положение
Фазовая карта циркулярно поляризованного пучка с двумя вихрями одного знака представлена на рис. 4.19. На этом же рисунке приведено положение  -контура, образующегося при суперпозиции такого пучка с ортогонально поляризованной плоской волной.
-контура, образующегося при суперпозиции такого пучка с ортогонально поляризованной плоской волной.
В соответствии с [82; 83] две дисклинации возникают на  -контуре. Можно показать, что в случае симметричных распределений параметров вихревого и гладкого пучков структура этих дисклинаций абсолютно идентична. Как следствие, структура сингулярностей Умова – Пойнтинга должна быть также одинаковой.
-контуре. Можно показать, что в случае симметричных распределений параметров вихревого и гладкого пучков структура этих дисклинаций абсолютно идентична. Как следствие, структура сингулярностей Умова – Пойнтинга должна быть также одинаковой.
Две вихревые сингулярности перемещаются вдоль  -контура в одном направлении (см. рис. 4.20). В геометрическом центре области возникает дополнительная, пассивная сингулярность седлового типа с отрицательным индексом Пуанкаре. Эта сингулярность обеспечивает топологическую связь между одинаковыми позитивными вихревыми сингулярностями.
-контура в одном направлении (см. рис. 4.20). В геометрическом центре области возникает дополнительная, пассивная сингулярность седлового типа с отрицательным индексом Пуанкаре. Эта сингулярность обеспечивает топологическую связь между одинаковыми позитивными вихревыми сингулярностями.

Рис. 4.20
Поведение мгновенного вектора Умова – Пойнтинга для поля, содержащего
две  -точки одного знака.
-точки одного знака.
сингулярность обеспечивает топологическую связь между одинаковыми позитивными вихревыми сингулярностями.

 Поведение усредненного вектора Умова – Пойнтинга иллюстрируется рисунком 4.21 a. Мы видим, что характер распределения параметров поперечной компоненты не сильно отличается от случая с одной
Поведение усредненного вектора Умова – Пойнтинга иллюстрируется рисунком 4.21 a. Мы видим, что характер распределения параметров поперечной компоненты не сильно отличается от случая с одной  -точкой. Различия поведения нормированных параметров практически стираются, если расстояние между
-точкой. Различия поведения нормированных параметров практически стираются, если расстояние между  -точками мало (см. рис. 4.21 b). При этом необходимо помнить, что величина момента импульса поля в области с двумя близко расположенными
-точками мало (см. рис. 4.21 b). При этом необходимо помнить, что величина момента импульса поля в области с двумя близко расположенными  -точками вдвое больше, чем в случае с областью, содержащей одну
-точками вдвое больше, чем в случае с областью, содержащей одну  -точку. Кроме того, поведение мгновенного вектора Умова – Пойнтинга коренным образом отличается от аналогичного поведения этой характеристики поля в области с одной
-точку. Кроме того, поведение мгновенного вектора Умова – Пойнтинга коренным образом отличается от аналогичного поведения этой характеристики поля в области с одной  -точкой (рис. 4.22).
-точкой (рис. 4.22).

a b c d
Рис. 4.22
Распределение параметров мгновенного вектора Умова – Пойнтинга для поля, содержащего две близко расположенные  -точки одного знака.
-точки одного знака.
d. Элементарные поляризационные ячейки с двумя  -точками разного знака
-точками разного знака
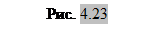
 Фазовая карта циркулярно поляризованного пучка с двумя вихрями разного знака представлена на рисунке 4.23. Вихри расположены на том же расстоянии, что и для поля, содержащего две одинаковые
Фазовая карта циркулярно поляризованного пучка с двумя вихрями разного знака представлена на рисунке 4.23. Вихри расположены на том же расстоянии, что и для поля, содержащего две одинаковые  -точки. Там же приведено положение
-точки. Там же приведено положение  -контура, образующегося при суперпозиции такого пучка с ортогонально поляризованной плоской волной. Как видим, положение
-контура, образующегося при суперпозиции такого пучка с ортогонально поляризованной плоской волной. Как видим, положение  -контура такое же, как и для области
-контура такое же, как и для области  -точек одного знака.
-точек одного знака.
Как и в предыдущем случае, на  -контуре возникают две сингулярности вектора Умова – Пойнтинга, ассоциируемые с дисклинациями поля. Однако одна из них вихревая (на
-контуре возникают две сингулярности вектора Умова – Пойнтинга, ассоциируемые с дисклинациями поля. Однако одна из них вихревая (на

a b c d
Рис. 4.24
Поведение мгновенного вектора Умова – Пойнтинга для поля, содержащего
две  -точки разного знака.
-точки разного знака.
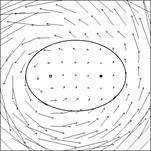 рисунке b она слева), а вторая пассивная, отрицательная (на рисунке b она справа). Кроме того, эти сингулярности перемещаются вдоль
рисунке b она слева), а вторая пассивная, отрицательная (на рисунке b она справа). Кроме того, эти сингулярности перемещаются вдоль  -контура в противоположных направлениях.
-контура в противоположных направлениях.
 В процессе движения (рис. 4.24) эти сингулярности аннигилируют (рис. c) и вновь появляются (рис. а). Поведение азимута поперечной компоненты вектора Умова – Пойнтинга для обеих ситуаций характеризуется отсутствием каких бы то ни было дефектов вдоль
В процессе движения (рис. 4.24) эти сингулярности аннигилируют (рис. c) и вновь появляются (рис. а). Поведение азимута поперечной компоненты вектора Умова – Пойнтинга для обеих ситуаций характеризуется отсутствием каких бы то ни было дефектов вдоль  -контура. Изменение азимута как функция параметра
-контура. Изменение азимута как функция параметра  -контура не претерпевает разрывов вдоль контура также в случае, когда дисклинации на
-контура не претерпевает разрывов вдоль контура также в случае, когда дисклинации на  -контуре отсутствуют (рис. d). Вместе с тем, модуль поперечной компоненты вектора Умова – Пойнтинга практически равен нулю в окрестности
-контуре отсутствуют (рис. d). Вместе с тем, модуль поперечной компоненты вектора Умова – Пойнтинга практически равен нулю в окрестности  -точки (правая
-точки (правая  -точка), для которой знак топологического заряда такой же, как знак handedness фактора в области, ограниченной
-точка), для которой знак топологического заряда такой же, как знак handedness фактора в области, ограниченной  -контуром. В точке поля, с координатами совпадающими с
-контуром. В точке поля, с координатами совпадающими с  -точкой, наблюдается пассивная сингулярность компоненты вектора Умова – Пойнтинга.
-точкой, наблюдается пассивная сингулярность компоненты вектора Умова – Пойнтинга.
Поведение параметров усредненного вектора Умова – Пойнтинга представлено на рисунке 4.25.
Видим, что вихревая сингулярность локализована в позиции  -точки, для которой выполняется соотношение
-точки, для которой выполняется соотношение  (левая
(левая  -точка) и модуль поперечной составляющей вектора Умова – Пойнтинга практически равен нулю в области
-точка) и модуль поперечной составляющей вектора Умова – Пойнтинга практически равен нулю в области  -точки, у которой знак топологического заряда такой же, как знак handedness фактора (правая
-точки, у которой знак топологического заряда такой же, как знак handedness фактора (правая  -точка).
-точка).
4.3.2.2. неСимметричные распределения амплитуд и фаз интерферирующих пучков
Покажем, что позиции сингулярных точек усредненной поперечной компоненты вектора Умова – Пойнтинга сдвигаются относительно позиций  -точек при несимметричных распределениях модуля амплитуды и фазы в интерферирующих пучках. Этот эффект наблюдается даже для области, содержащей одну
-точек при несимметричных распределениях модуля амплитуды и фазы в интерферирующих пучках. Этот эффект наблюдается даже для области, содержащей одну  -точку.
-точку.
Сдвиг сингулярности относительно  -точки возникает, когда оба или даже один из интерферирующих пучков обладает асимметрией распределения фазы или амплитуды (в дальнейшем просто асимметрией) относительно позиции
-точки возникает, когда оба или даже один из интерферирующих пучков обладает асимметрией распределения фазы или амплитуды (в дальнейшем просто асимметрией) относительно позиции  -точки. Можно показать, что главным фактором, определяющим величину сдвига, является не сама величина асимметрии, а взаимное соотношение фаз, отношений модулей амплитуд, ассоциируемых с каждым пучком. Таким образом, для установления закономерностей влияющих на величину сдвига сингулярности вектора Умова – Пойнтинга относительно
-точки. Можно показать, что главным фактором, определяющим величину сдвига, является не сама величина асимметрии, а взаимное соотношение фаз, отношений модулей амплитуд, ассоциируемых с каждым пучком. Таким образом, для установления закономерностей влияющих на величину сдвига сингулярности вектора Умова – Пойнтинга относительно  -точки, достаточно вносить изменение фазы или интенсивности только в один из пучков. Поэтому будем вносить изменения в параметры только одного из пучков, например гладкого. Можно показать, что в этом случае усредненные
-точки, достаточно вносить изменение фазы или интенсивности только в один из пучков. Поэтому будем вносить изменения в параметры только одного из пучков, например гладкого. Можно показать, что в этом случае усредненные 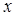 - и
- и 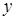 -компоненты вектора Умова – Пойнтинга описываются следующим выражением.
-компоненты вектора Умова – Пойнтинга описываются следующим выражением.
 , (4.26)
, (4.26)
где 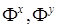 – производные по фазе гладкого пучка;
– производные по фазе гладкого пучка; 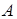 – его модуль амплитуды;
– его модуль амплитуды;  – относительные изменения модуля амплитуды.
– относительные изменения модуля амплитуды.
Из соотношения (4.26) следует, что сдвиг нуля поперечной компоненты вектора Умова – Пойнтинга определяется как градиентом фазы опорного пучка, так и градиентом относительных изменений его амплитуды. Отличие заключается лишь в том, что 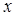 -,
-, 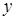 -изменения в фазе влияют на одноименную компоненту вектора, а изменения модуля амплитуды на противоположную.
-изменения в фазе влияют на одноименную компоненту вектора, а изменения модуля амплитуды на противоположную.
Предположим, что в зоне анализа вносимые изменения не очень велики и выполняется линейное приближение – как для модуля амплитуды, так и для фазы пучка.
Именно такое условие было положено в основу цифрового моделирования.

Рис. 4.26
Сдвиг сингулярности поперечной компоненты вектора Умова – Пойнтинга под воздействием фазовой асимметрии в опорном пучке.
a – распределение модуля поперечной компоненты, b – распределение азимута составляющей. Азимут поперечной составляющей вектора на рисунках (с) соответствует ориентации стрелок, величина ее модуля иллюстрируется длиною стрелок:
1 – «нуль» асимметрии;
2 – «незначительная» фазовая асимметрия гладкого пучка;
3 – «значительная» фазовая асимметрия опорного пучка.
Рисунки 4.26 – 4.28 иллюстрируют изменения в поле вектора Умова – Пойнтинга, которые соответствуют различным значениям асимметрии, вносимой в опорный пучок. Для простоты сравнения результатов в строке 1 приведены распределения параметров вектора Умова – Пойнтига для поля, сформированного симметричными пучками.
Рисунки (a) иллюстрируют поведение модуля поперечной составляющей вектора Умова – Пойнтинга результирующего поля. Столбец (b) – карты азимутов компоненты вектора Умова – Пойнтинга. На рисунках (с) представлено распределение как модуля, так и азимута. На ориентацию вектора указывает направление стрелок, величина модуля составляющей иллюстрируется длиною стрелок.

Рис. 4.27
Сдвиг сингулярности поперечной компоненты вектора Умова – Пойнтинга под воздействием асимметрии модуля амплитуды в опорном пучке.
a – распределение модуля поперечной компоненты; b – распределение азимута составляющей. Азимут поперечной составляющей вектора на рисунках (с) соответствует ориентации стрелок, величина ее модуля иллюстрируется длиною стрелок:
1 – «нуль» асимметрии;
2 – «незначительная» асимметрия модуля амплитуды гладкого пучка;
3 – «значительная» асимметрия модуля амплитуды опорного пучка.
На рисунке 4.26 представлено влияние фазовой асимметрии на позицию сингулярности вектора Умова – Пойнтинга.
Как видим, при определенной величине асимметрии сингулярность поперечной составляющей может сдвинуться относительно позиции  -точки даже за границу
-точки даже за границу  -контура, переместившись в область с другим типом эллиптической поляризации.
-контура, переместившись в область с другим типом эллиптической поляризации.

Рис. 4.28
Сдвиг сингулярности поперечной компоненты вектора Умова – Пойнтинга под воздействием обоих типов асимметрии опорного пучка
a – распределение модуля поперечной компоненты; b – распределение азимута составляющей. Азимут поперечной составляющей вектора на рисунках (с) соответствует ориентации стрелок, величина ее модуля иллюстрируется длиною стрелок:
1 – «нуль» асимметрии;
2 – «незначительная» асимметрия гладкого пучка;
3 – «значительная» асимметрия опорного пучка.
Рисунок 4.27 иллюстрирует возникновение сдвига сингулярности под воздействием амплитудной асимметрии.
На рисунке 4.28 представлены данные компьютерного моделирования, подтверждающего сдвиг сингулярности вектора Умова – Пойнтинга под влиянием обоих типов асимметрии.
Таким образом, благодаря фазовой или амплитудной асимметрии, возникшей хотя бы в одном из интерферирующих пучков, сингулярность поперечной составляющей вектора Умова – Пойнтинга, а значит, и точка приложения максимального усредненного момента импульса поля, сдвигается относительно позиции  -точки.
-точки.
Очевидно, что такой сдвиг характерен не только для элементарных поляризационных ячеек, но и для неоднородно поляризованных полей общего вида.
Естественно, что соответствующую асимметрию интерферирующих пучков можно «вводить» искусственно, путем формирования специальных гладких или вихревых пучков, например, с помощью использования специальных синтезированных голограмм. Такие голограммы могут быть сформированы и на оперативном носителе типа пространственно-временной модулятор света. Тогда, по нашему мнению, возникает реальная возможность создания светлой поляризационно-неоднородной ловушки с управляемой точкой приложения орбитального момента импульса поля.
4.3.2.3. Экспериментальное подтверждение существования орбитального момента импульса в области  -точки
-точки

 Элементарная поляризационная ячейка с
Элементарная поляризационная ячейка с  -точкой в середине области, ограниченной замкнутым
-точкой в середине области, ограниченной замкнутым  -контуром, была сформирована методом суперпозиции циркулярно поляризованного вихревого пучка и ортогонально поляризованной опорной волны с Гауссовым распределением интенсивности [106 – 110]. При этом знак топологического заряда вихря не совпадал со знаком handedness фактора вихревого пучка. В этом случае результирующее поле обладает характерным распределением поляризационных характеристик (см. рис. 4.29.
-контуром, была сформирована методом суперпозиции циркулярно поляризованного вихревого пучка и ортогонально поляризованной опорной волны с Гауссовым распределением интенсивности [106 – 110]. При этом знак топологического заряда вихря не совпадал со знаком handedness фактора вихревого пучка. В этом случае результирующее поле обладает характерным распределением поляризационных характеристик (см. рис. 4.29.
Исходя из рассмотрения, проведенного в п. 4.3.2.1. b, в области  -точки должен существовать орбитальный момент импульса поля.
-точки должен существовать орбитальный момент импульса поля.
Поскольку формирование элементарной поляризационной ячейки не составляет особого труда в экспериментальном аспекте, то главной задачей при проверке теоретических предположений являлось правильно выбрать «индикатор» присутствия орбитального момента импульса в области «тестового» поля.
К сожалению, выбор возможных вариантов идентификации орбитального момента достаточно невелик (см., например, [100]). С точки зрения вариантов, наиболее подходящих к нашим экспериментальным условиям, оптимальным являлся метод, основанный на явлении передачи момента импульса поля некоторой механической системе, на которую воздействует электромагнитная волна.
Такая идентификация орбитального момента импульса основана на следующих фактах:
1. Как известно (см., например, [104]), при фокусировке лазерного пучка возникает оптическая ловушка, способная захватить и удерживать микрообъект.
2. При этом наблюдается вращение захваченного микрообъекта, если поле обладает спиновым или орбитальным моментом импульса (см., например, [102; 103]). Главным фактором, влияющим на частоту вращения, является величина этого момента, а направление вращения определяется знаком момента.
3. В общем случае сфокусированный пучок обладает как спиновым, так и орбитальным моментом импульса поля. Частота вращения микрообъекта будет максимальной, если знаки спинового и орбитального моментов будут совпадать, и она будет минимальной (возможно даже прекращение вращения или изменение его направления), если эти знаки разные (спиновый момент импульса компенсирует орбитальный).
 Таким образом, если сфокусировать неоднородно поляризованный пучок, сформированный в результате суперпозиции циркулярно поляризованных пучков, образуется поляризационно неоднородная оптическая ловушка, способная захватывать и вращать микрообъект. При этом характеристики вращения будут меняться, если изменять параметры интерферирующих пучков, например знак вихревого пучка или его handedness фактор.
Таким образом, если сфокусировать неоднородно поляризованный пучок, сформированный в результате суперпозиции циркулярно поляризованных пучков, образуется поляризационно неоднородная оптическая ловушка, способная захватывать и вращать микрообъект. При этом характеристики вращения будут меняться, если изменять параметры интерферирующих пучков, например знак вихревого пучка или его handedness фактор.
 Экспериментальное расположение (рис. 4.30), используемое для идентификации орбитального момента импульса поля подобно, описанному в п. 3.5, отличается от него тем, что на выходе интерферометра, формирующего элементарную поляризационную ячейку, устанавливаются устройства для фокусировки пучков и наблюдения результатов воздействия поля на микрочастицу.
Экспериментальное расположение (рис. 4.30), используемое для идентификации орбитального момента импульса поля подобно, описанному в п. 3.5, отличается от него тем, что на выходе интерферометра, формирующего элементарную поляризационную ячейку, устанавливаются устройства для фокусировки пучков и наблюдения результатов воздействия поля на микрочастицу.
Линейно поляризованный пучок He-Ne лазера направляется в интерферометр Маха – Цандера (элементы 2 – 8). Этот пучок преобразуется в ортогонально циркулярно поляризованные пучки с помощью четвертьволновых пластинок 3, 6. Один из них проходит через вихревую компьютерно-  синтезированную голограмму 7. После этой голограммы возникает циркулярно поляризованный вихрь 4.
синтезированную голограмму 7. После этой голограммы возникает циркулярно поляризованный вихрь 4.
Поляризационно-неоднородное поле, содержащее  -точку формируется на выходе интерферометра.
-точку формируется на выходе интерферометра.

 Далее результирующее поле фокусируется с помощью микрообъектива 11 в плоскость образца с микрочастицами 12. Результат воздействия пучка на микрообъекты наблюдается с помощью оптической системы 13, 14 с CCD-камерой. Для формирования оптической ловушки использовался
Далее результирующее поле фокусируется с помощью микрообъектива 11 в плоскость образца с микрочастицами 12. Результат воздействия пучка на микрообъекты наблюдается с помощью оптической системы 13, 14 с CCD-камерой. Для формирования оптической ловушки использовался  -микрообъектив с единичной апертурой. Поперечные размеры ловушки составляли 8 – 10 мкм.
-микрообъектив с единичной апертурой. Поперечные размеры ловушки составляли 8 – 10 мкм.
 Для сохранения поляризационных характеристик сформированного в интерферометре поля было выбрано горизонтальное экспериментальное расположение. Благодаря этому действующий пучок только проходил через оптические поверхности, но не отражался от них. В этом случае поляризационная структура пучка в плоскости образца оставалась практически такой же, как и на выходе интерферометра.
Для сохранения поляризационных характеристик сформированного в интерферометре поля было выбрано горизонтальное экспериментальное расположение. Благодаря этому действующий пучок только проходил через оптические поверхности, но не отражался от них. В этом случае поляризационная структура пучка в плоскости образца оставалась практически такой же, как и на выходе интерферометра.
Знак (направление воздействия поля в поперечной плоскости) орбитального момента импульса мог легко меняться выбором дифракционного порядка после вихревой голограммы 7. Известно (см. [37 – 39] и п. 1.4), что вихри, сформированные в положительных и отрицательных дифракционных порядках, отличаются знаком топологического заряда.
Рисунок 4.31 иллюстрирует распределение интенсивностей циркулярно поляризованных компонент результирующего поля.
Анализатор 9 мог вводиться в пучок после интерферометра с целью визуализации поляризационной модуляции в ловушке. Распределения интенсивностей линейно поляризованных проекций результирующего поля для различной ориентации анализатора приведены на рисунке 4.32.
Темное пятно на границе ловушки на каждом рисунке соответствует позиции вихря поляризационной проекции (белая точка на рисунках).
Эти точки также идентифицируют координаты точек в которых наблюдаются наевские дисклинации, движущиеся вдоль  -контура под действием временных изменений векторного поля. Как видно из рисунка 4.32, интенсивности вихревого и гладкого пучков были подобраны таким образом, что
-контура под действием временных изменений векторного поля. Как видно из рисунка 4.32, интенсивности вихревого и гладкого пучков были подобраны таким образом, что  -контур располагался практически по краю ловушки. Благодаря этому область с одним значением handedness фактора и соответственно с одним направлением спинового момента импульса реализуется практически по всей области ловушки.
-контур располагался практически по краю ловушки. Благодаря этому область с одним значением handedness фактора и соответственно с одним направлением спинового момента импульса реализуется практически по всей области ловушки.
Дата добавления: 2015-07-12; просмотров: 124 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сети вихрей – скелетон фазы скалярного поля 9 страница | | | Сети вихрей – скелетон фазы скалярного поля 11 страница |