Сети вихрей – скелетон фазы скалярного поля 5 страница

Точки -контура в которых наблюдается экстремум азимута поляризации достаточно просто идентифицировать с помощью анализа вихревых сеток последовательности линейно поляризационных проекций векторного поля.

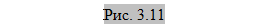
Рассмотрим участок -контура (рис. 3.11 a – e), где отображено. поведение азимута линейной поляризации (рис. 3.11 a). Изменение азимута вдоль -контура схематически представлено на рисунке f. Как видим (рис. a и f), в точке 3 наблюдается локальный минимум азимута. С помощью вращающегося поляризатора будем выделять из поля различные линейно поляризованные проекции. Направление вращения указано стрелкой в правой части рисунка а. Рисунки b – e соответствуют четырем различным положениям поляризатора. Ориентация его оси совпадает с направлением жирных стрелок в правой части рисунков. В ситуации, представленной рисунком b, положение поляризатора такое, что он не пропускает излучение с поляризацией, азимут которой такой же как в точках 1’ и 1’’. В этом случае в этих точках поля поляризационной проекции образуются вихри. Можно показать, что эти вихри разных знаков. Идентификация вихрей может быть произведена, если, например, организовать интерференцию поляризационной проекции поля с опорной волной. Тогда в местах локализации вихрей будут наблюдаться интерференционные вилочки. Дальнейший поворот поляризатора (ситуация (с)) приведет к сдвигу вихрей проекции вдоль -контура из положений 1’,1’’ в положения 2’,2’’. И, наконец, при ориентации, указанной на рисунке (d) вихри сольются и аннигилируют. Дальнейший, даже небольшой поворот поляризатора приведет к тому, что на участке -контура не будет наблюдаться ни одного вихря (рис. 3.11 e).

С помощью подобной методики можно фактически проводить «визуализацию» дисклинации в произвольной точке -контура.

Действительно, рассмотрим разложение 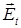на ортогональные компоненты 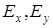. Сориентируем одну из осей системы координат в произвольной точке -контура по направлению вектора 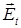. Тогда одна из компонент (допустим, 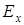) тождественно равна нулю в любой момент времени (образуется вихрь этой компоненты). Соответственно поперечная компонента электрического поля в этой точке описывается выражением

. (3.21)

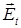Таким образом, при ориентации одной из осей базиса разложения вдоль вектора , в этой точке на -контуреусловие возникновения дисклинации будет таким:

(3.22)

Условие появления дисклинации, приведенное в [77], имеет вид:

(3.23)

Сравнивая (3.22) и (3.23), видим, что на -контуре 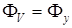. Тогда используя поляризатор, сориентированный так, что пропускается компонента 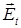с азимутом вдоль оси 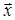, будем наблюдать вихрь 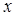- компоненты, тем самым «визуализируя» дисклинацию соответствующую моменту времени . может быть определена интерференционно (естественно с точностью до фазы опорного пучка) при повороте поляризатора на 90 градусов. Повернем поляризатор на небольшой угол относительно первоначального положения. Соответственно вихрь компоненты 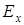переместится вдоль -контура, что даст возможность визуализировать дисклинацию в другой момент времени. Таким образом, можно установить соответствие между положением (как функции времени) дисклинации на -контуре и поворотом азимута поляризатора, положением вихря (как функции пространственных координат).

Экспериментально процессы рождения и аннигиляции вихрей поляризационных проекций поля можно наблюдать в интерферометре типа Маха – Цандера, изображенного на рисунке 3.12 [82 – 85].

В объектный пучок в фокальную плоскость микрообъектива 2 помещается образец – тефлоновая пластинка – среда, в которой реализуется многократное рассеяние. Пластинка достаточно тонкая. Поэтому когерентность пучка лазера практически не разрушается, а сфокусированный пучок освещает ограниченное количество рассеивающих центров. В такой ситуации размеры светового пятна непосредственно за рассеивателем остаются практически такими же, как размеры перетяжки сфокусированного пучка. За объектом, на фокусном расстоянии располагается объектив 4, за которым формируется квазипараллельный пучок и таким образом реализуется (в том числе и в плоскости 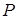) приближение дальней зоны. В опорный канал помещается пластинка , преобразующая линейную поляризацию опорного пучка в циркулярную. На выходе интерферометра устанавливается вращающийся анализатор 12 для выделения произвольной проекции объектного пучка и опорной волны. В плоскости 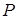наблюдается результат интерференции произвольных проекций векторного поля и соответствующих им проекций опорного пучка.

Рассмотрим результаты эксперимента (рис. 3.13). С левой стороны рисунков светлой стрелкой обозначен пространственный репер. Все полосы интерференционной картины непрерывные в границах поля интерферограммы (рис. 3.13 a). При некотором повороте оси пропускания поляризатора 12 в зоне, обозначенной белым прямоугольником, появляется ярко выраженный изгиб интерференционной полосы, свидетельствующий о резком изменении фазы в этом районе поля. При дальнейшем повороте поляризатора 12 в этом месте возникает разрыв полосы, соответствующий точке рождения вихрей (рис. 3.13 с). В этой точке, как было показано выше, наблюдается локальный экстремум азимута 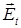. На этом же рисунке можно видеть, что в зону анализа входит новый вихрь (направленная вниз интерференционная вилочка). Дальнейшее вращение анализатора приводит к тому, что от точки рождения вихрей в противоположных направлениях движутся вихри разных знаков 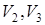(рис. 3.13 d). На этом же рисунке в зоне, ограниченной белым прямоугольником, можно наблюдать новый «разрыв» интерференционной полосы, отвечающий точке рождения еще одной пары вихрей. На рис. 3.13 е в зоне, выделенной прямоугольником, вихрь проаннигилировал с правым рожденным вихрем, а вихрь движется в направлении вихря 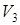. Процесс аннигиляции вихре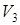й и уже совершился, и по всей плоскости анализа наблюдаются непрерывные интерференционные полосы, за исключением зоны вихря , продолжающего смещаться в направлении левого угла интерферограммы (рис. 3.13 f). Светлой линией на этом рисунке обозначено положение -контура.

3.3.4. -точки как вихри разности фаз.

Разложим векторное поле на ортогональные циркулярно поляризованные компоненты. Естественно, что и в этом случае получим полную систему вихрей (суперпозицию двух сетей вихрей), анализ которой позволяет установить связь между вихрями компонент и векторными сингулярностями. Однако при таком разложении, по сравнению с разложением на линейно поляризованные компоненты, отмечаются некоторые особенности:

1. Как известно, разность фаз между компонентами не зависит от ориентации базиса разложения.

2. В роли вихрей разности фаз в этом случае выступают -точки (см. п. 3.2.1).

3. Как следует из соотношения (3.3), контуры разности фаз соответствуют линиям постоянного азимута поляризации.

При таком разложении поля -контуры – линии, которые определяются решениями уравнения . Как и для разложения на линейно поляризованные компоненты, для случая разложения на циркулярно поляризованные компоненты вихрям разности фаз можно поставить в соответствие топологические заряды. Топологический заряд такого вихря по знаку совпадает с индексом -точки, а его модуль в два раза больше.

Очевидно, что для C -точек как вихрей разности фаз (с учетом (3.2) и (3.3)) может быть сформулирован знаковый принцип, аналогичный знаковому принципу фазовых вихрей скалярного поля, и вихрей разности фаз, полученных при разложении векторного поля на линейно поляризованные компоненты [83; 86; 87]:

1. На замкнутой линии равных азимутов находится четное количество -точек.

2. Соседние -точки, находящиеся на одной линии равных азимутов, характеризуются индексами 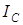разных знаков.

Естественно, что выполняются следующие топологические инварианты:

1. Количество -точек (вихрей разности фаз) с топологическим индексом одного знака равняется количеству -точек (количеству вихрей) противоположного знака:

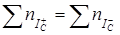. (3.24)

2. Количество седловых точек поля азимутов с количеством экстремумов азимута и -точек связано соотношением:

. (3.25)

Количество экстремальных точек азимута поляризации (экстремумов разности фаз) значительно меньше, чем количество - точек и седел. Этот факт снова следует из свойств оценочного скалярного поля , которое можно ввести аналогично случаю разложения на линейно поляризованные компоненты.

Практическое отсутствие экстремумов азимута поляризации как точек, в которых азимут принимает максимальное или минимальное значение, не противоречит присутствию локальных экстремумов азимута линейной поляризации вдоль -контура (рис. 3.14). Штриховыми линиями на рисунке обозначены -контуры. Штрихпунктирными (с одной и двумя точками) обозначены касательные к ним линии постоянного азимута. Как видим из рисунка, именно в этих точках касания 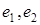, наблюдаются локальные экстремумы азимута линейной поляризации.

3.4. «Корреляция» между интенсивностью и поляризацией векторного поля

Как было показано в п. 2.6, поведение фазы и интенсивности скалярного поля взаимосвязаны. Очевидно, что из этого факта должна вытекать связь между распределением интенсивности и поляризационных характеристик векторного поля, поскольку изменения фазы и интенсивности ортогональных компонент как скалярных полей «антискоррелированы» [83].

Можно показать, что модуль градиента интенсивности векторного поля описывается соотношением:

, (3.26)

где – модули комплексных амплитуд и их частные производные право- и левоциркулярно поляризованных компонент.

Квадрат модуля градиента отношения модулей право- и левоциркулярно поляризованных компонент имеет вид:

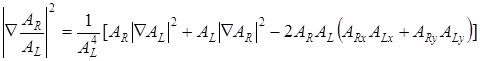. (3.27)

Очевидно, что для области поля, в которой наблюдаются незначительные изменения поляризации, должны выполняться условия:

, (3.28)

где – разность фаз между право- и левополяризованными компонентами. Из первого уравнения (3.28) и соотношений (3.26, 3.27) следует, что в области незначительных изменений поляризации градиент интенсивности подчиняется соотношению:

. (3.29)

Пусть средние значения модулей амплитуды право- и левополяризованных компонент отличаются коэффициентом e. Тогда, учитывая, что независимые случайные величины и их средние значения равняются нулю, можно получить средний градиент интенсивности для всего поля:

, (3.30)

и для областей с незначительными изменениями поляризации:

. (3.31)

Из (3.30) и (3.31) следует, что отношение таких средних градиентов будет таким:

. (3.32)

Из (3.32) следует, что в областях поля с незначительными изменениями поляризации модуль градиента интенсивности в среднем в раз больше чем в остальных областях поля. Так, для «полностью деполяризованного» поля, поля с одинаковыми значениями средних интенсивностей компонент () .

Иными словами, в векторном поле малым изменениям поляризации соответствуют быстрые изменения интенсивности.

Рассмотрим данные компьютерного моделирования (рис. 3.15). На рисунке (a) приведено распределение интенсивности случайного векторного поля с одинаковыми средними значениями интенсивности право- и лево- циркулярно поляризованных компонент. Уровень интенсивности соответствует различным градациям серого цвета.

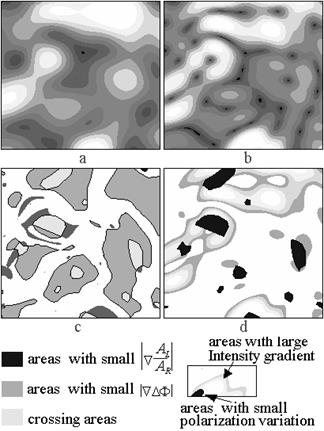
Рисунок (b) – поведение градиента интенсивности. Рисунок (c) иллюстрирует положение областей с незначительными изменениями поляризации. Темные области – области поля с малым градиентом отношения модулей амплитуд право- и лево- циркулярно поляризованных компонент . Более светлый оттенок серого соответствует областям с малым градиентом разности фаз. Светло-серый цвет – области перекрытия этих регионов (области поля с незначительными изменениями поляризации). Наконец, на рисунке (d) показаны области поля с медленными изменениями поляризации (темные области) и регионы с быстрым изменением интенсивности.

Как следует из рисунка (d) области поля, в которых поляризация изменяется мало, «стремятся» к областям с большим градиентом интенсивности.

3.5. Связь между вихрями компонент и -точками

Вновь представим векторное поле как сумму двух ортогональных линейно поляризованных компонент 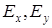. Соответственно комплексные амплитуды 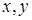-компонент связаны с параметрами ортогональных циркулярно поляризованных компонент соотношением [3; 81]:

(3.33)

где 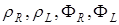– модули амплитуд и фазы право и лево циркулярно поляризованных компонент.

Пусть -контур ограничивает область с одним типом (для определенности правой) поляризацией (Рис. 3.16). В точках -контура, где оси базиса разложения параллельны направлению колебания поля, компоненты имеют вихри , .

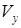Рассмотрим подробно одну из компонент ( -компоненту для определенности). Соотношение (3.33) для -компоненты может быть переписано в виде

. (3.34)

Для линейной поляризации ( -контур, )

. (3.35)

В представлении разложения поля на линейно поляризованные компоненты

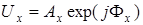. (3.36)

Заметим, что – непрерывная, гладкая вдоль -контура функция. не определена в сингулярных точках и изменяется на при переходе через вихрь. Сингулярная точка соответствует азимуту 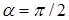в выражении (3.35). Изменение знака косинуса при переходе через эти точки как раз и соответствует добавлению или отниманию постоянной фазы, равной . Перепишем (3.35) в виде

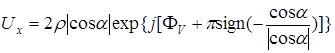, (3.37)

где .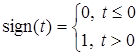

Из (3.37) следует, что:

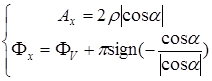. (3.38)

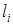Разделим -контур на участки , на которых – непрерывная, гладкая функция и участки, включающие линейную поляризацию с азимутом, равным 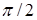(вихри -компоненты). Длина участков -контура, включающих вихри , невелика и стремится к нулю. Рассмотрим сумму

, (3.39)

где 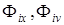– соответствующие фазы на участках 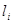; – количество вихрей -компоненты вдоль -контура.

Дифференциал от (3.39) имеет вид

. (3.40)

Проинтегрируем (3.40) вдоль отрезков 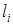-контура. Направление интегрирования – против часовой стрелки:

. (3.41)

Рассмотрим интеграл вдоль полуокружности радиусом 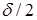(рис. 3.17; ситуации a,b) в области, включающей вихрь -компоненты. В силу малости справедливо линейное приближение при описании поля в этой области. Тогда, вследствие периодичности изменения , при обходе сингулярной точки по окружности (период см. п. 1.1) этот интеграл равен:

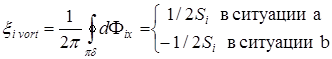. (3.42)

Прибавим к левой и правой части (3.41) величину:

, (3.43)

где – суммарный топологический заряд -вихрей, расположенных на -контуре. При этом интегрирование по полуокружностям совершалось по типу a-ситуаций. Тогда величина соответствует интегралу от по некоторому замкнутому -контуру, вдоль которого является непрерывной функцией:

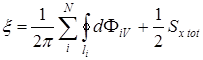. (3.44)

Область, ограниченная таким контуром, содержит все -точки, лежащие в области правой поляризации, и вихри -компоненты, расположенные вдоль -контура. Предполагается, что настолько мало, что -точки, лежащие в области с левой поляризацией, не попадают в зону, ограниченную -контуром.

Из (3.10) следует, что интеграл вдоль -контура от равен суммарному топологическому заряду -точек в области, им ограниченной:

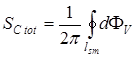. (3.45)

Кроме того в силу непрерывности вдоль -контура и малости , справедливо соотношение:

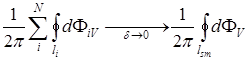. (3.46)

С другой стороны [3; 11],

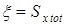. (3.47)

Тогда из (3.45)-(3.47) следует соотношение

. (3.48 a)

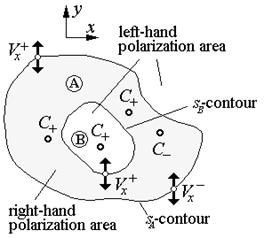Соотношение (3.48 a) может быть получено также в предположении, что выражение типа (3.43) вычисляется при использовании процедуры b (см. рис. 3.17). Тогда замкнутый контур интегрирования 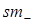-контур ограничивает область, которая не содержит -вихрей. Интеграл от по такому контуру равен нулю, и имеет место выражение

, (3.48b)

которое совпадает с (3.48 a).

Можно показать, что поскольку -компонента поля была выбрана произвольно, то и для вихрей 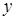-компоненты их суммарный топологический заряд вдвое больше суммарного топологического индекса С-точек:

. (3.49)

Теперь предположим, что рассматриваемый 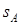-контур ограничивает область с правой поляризацией A, внутри которой находится область с левой поляризацией B (рис. 3.18). Граница между областями A и B – -контур. Суммарный топологический индекс -точек в области B равняется половине суммарного топологического заряда -вихрей, расположенных на -контуре:

Дата добавления: 2015-07-12