Сети вихрей – скелетон фазы скалярного поля 4 страница

Напомним, что суммарный топологический индекс в области равен сумме элементарных индексов и может быть получен из соотношения:

, (3.10)

где – односвязная замкнутая линия, охватывающая все сингулярности.

Выберем в качестве контура -контур. Тогда из (3.10) следует взаимосвязь - и -синуглярностей, суть которой заключается в том, что полное количество и направление оборотов вектора линейной поляризации вдоль -контура совпадает с суммарным индексом -точек 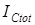, ограниченных этим контуром. Так, например, для рисунка 3.6 суммарный топологический индекс -точек в области ограниченной -контуром , что соответствует повороту на вектора поля при полном обходе контура против часовой стрелки.

Иными словами, поляризационная ситуация внутри области гомеоморфно отражается на -контур, и параметры -, и -синуглярностей определяют характер поведения поля в любой точке области.

Таким образом, можно утверждать, что, как и в случае скалярного поля, система стационарных (поляризационных) сингулярностей формирует скелетон векторного поля, «определяющий» его поведение в любой его точке.

3.3. Вихри разности фаз. Знаковый принцип для векторного поля

3.3.1. Разложение поля на линейно поляризованные ортогональные компоненты

Как было показано в предыдущем параграфе, поляризационные сингулярности и дисклинации взаимосвязаны. Областью существования дисклинаций являются -контуры. В процессе своего движения дисклинации пробегают каждую точку -множества [3; 65]. Одновременно с этим в работе [77] показано, что топология дисклинаций зависит от присутствия и распределения -точек в области, ограниченной -контуром. С другой стороны, очевидно, справедливым является обратное утверждение, что именно дисклинации определяют поведение поляризационных сингулярностей.

Таким образом, дисклинации и поляризационные сингулярности чрезвычайно жестко связаны и взаимно определяют характеристики друг друга. Однако, как уже было отмечено ранее, дисклинации в оптическом эксперименте недоступны прямому наблюдению вследствие быстрых изменений поля во времени.

Именно поэтому было бы целесообразно перейти от системы дисклинаций к системе некоторых стационарных сингулярностей-аналогов дисклинаций, которая смогла бы заменить систему временных точечных дефектов поля и была аналогично связана с - и -сингулярными множествами. Иными словами, при построении новой системы сингулярностей необходимо перейти от временных характеристик к пространственным, например, как это делается в традиционной оптике при описании состояния эллиптической поляризации поля в терминах модулей амплитуд ортогональных компонент и разности фаз между ними [28; 80]. Таким образом, новая система сингулярностей должна быть связана с системами сингулярностей ортогональных компонент, к анализу которых применим «скалярный» подход.

Как было показано в разделе 2, такой системой для скалярных компонент векторного поля являются сети фазовых вихрей, характеризующие топологическую структуру компонент, определяющие поведение фазы и интенсивности.

Поскольку каждая из ортогональных компонент определяется своею сетью вихрей, то следует ожидать, что векторное поле должно характеризоваться их суперпозицией, т.е. «полной» системой фазовых вихрей. Анализ такой системы будем называть «вихревым» анализом векторного поля. Задачей анализа является установление связи между полной системой вихрей и поляризационными сингулярностями, дисклинациями векторного поля. Еще раз подчеркнем, что в отличие от дисклинаций, фазовые вихри ортогональных компонент легко доступны прямому наблюдению, например интерференционными методами [8 – 10;12; 36 – 39].

Сначала покажем, что векторное поле в дальней зоне можно характеризовать общей сетью новых оптических вихрей – вихрей поля разности фаз. Такой подход, по сути, сводит векторное рассмотрение проблемы к скалярному.

3.3.2. Принципы вихревого анализа векторных полей

Покажем, что «вихри разности фаз» полностью определяют топологию векторного поля и это дает возможность установить соответствие между полной системой фазовых вихрей и поляризационными сингулярностями векторного поля.

Рассмотрим электромагнитную монохроматическую волну, распространяющуюся в свободном пространстве вдоль оси .

Известно, что вектор электрического поля можно описать соотношением [28]:

, (3.11)

где – комплексный вектор вида

. (3.12)

В дальней зоне можно пренебречь -компонентой электрического вектора. Тогда рассмотрение сведется к анализу поперечной компоненты поля 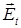. – гладкие функции двух координат 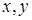, а описывается соотношением

, (3.13)

где 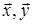– единичные векторы; , 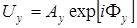– комплексные амплитуды ортогональных компонент; 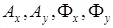– модули и фазы комплексных амплитуд соответственно.

Распространение волны вдоль сведется (с точностью до ) к масштабному преобразованию с некоторым коэффициентом, обусловленным расстоянием до рассеивающего объекта [11]. Заметим, что приближение дальней зоны не является принципиальным и рассмотрение можно легко распространить для зависимости от трех координат.

Выберем произвольным образом в плоскости наблюдения Декартову систему координат и введем некоторую характеристическую функцию:

, (3.14)

где ; .

Очевидно, что характеристическую функцию , заданную соотношением (3.14), можно интерпретировать как комплексную амплитуду некоторого скалярного поля, фаза которого совпадает с разностью фаз ортогональных компонент. Заметим, что поле типа (3.14) может быть физически реализовано, например, методами голографии. Вихри поля находятся в тех же точках, что и нули амплитуды ортогональных компонент, поскольку в этих точках или достигают своего нулевого значения. Естественно, что разность фаз в этих точках не определена, т.е. эти точки – сингулярные точки разности фаз. Более того, эти точки могут быть интерпретированы как вихри поля . Таким образом, топология фазы поля полностью определяет топологию разности фаз D j векторного поля.

Очевидно, что условие существования нулей амплитуды поля (как и для обычного скалярного поля) имеет вид:

(3.15)

Решения первого уравнения системы (3.15) определяют линии, вдоль которых или , т.е. лини, вдоль которых поляризация поля линейная. Таким образом, решения первого уравнения соответствует s -контурам. Кривые, которые получаются из второго уравнения, мы будем по аналогии называть “ -контурами”. Вдоль этих линий 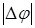равна и в точках, где располагаются -точки. Далее любые кривые, вдоль которых разность фаз постоянна, будем называть контурами этой разности фаз.

Отметим, что разность фаз вдоль - контура изменяется скачком на при переходе через вихрь. Подобно дислокациям волнового фронта, вихри разности фаз [82,83] могут характеризоваться двумя типами топологических индексов: индексом Пуанкаре и топологическим зарядом. Будем обозначать их и соответственно.

Естественно, что, как и в случае фазовых вихрей, .

Очевидно, что значение топологического заряда вихрей разности фаз связано со значением топологического заряда вихрей ортогональных компонент. Для определенности будем считать, что разность фаз вычисляется как разность фаз 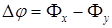, т.е. из фазы -ой компоненты вычитается фаза 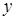-ой. Тогда эта связь устанавливается соотношением:

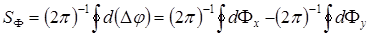. (3.16)

Как следует из уравнения (3.16), топологический заряд вихря разности фаз совпадает с зарядом вихря ортогональной компоненты, если вихрь разности фаз создан вихрем -компоненты и имеет противоположный знак по сравнению с вихрем компоненты, если он образован вихрем 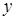-компоненты.

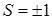В дальнейшем будем обозначать вихри компонент как ( и соответственно) и вихри разности фаз как (* и ~ ассоциируются с топологическими зарядами +1 и -1 соответственно).

Подчеркнем, что седловые точки поля разности фаз являются пересечениями только одной пары линий одинаковой разности фаз (топологически устойчивая структура) и соответственно и .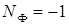

Применяя подход, используемый в [11] к полю разности фаз можно сформулировать следующие закономерности сохранения топологических инвариантов:

1. Количество вихрей разности фаз с топологическим зарядом одного знака равно количеству вихрей другого знака

. (3.17)

2. Количество седловых точек поля разности фаз связано с количеством экстремумов разности фаз и вихрей соотношением

. (3.18)

Заметим, что количество экстремальных точек поля разности фаз значительно меньше, чем количество вихрей и седел. Это факт непосредственно вытекает из свойств характеристической функции , ее интерпретации как скалярного поля. Как следует из п. 2.6, количество вихрей (седел) скалярного поля относится к количеству экстремумов фазы как .

Из интерпретации функции как скалярного поля также непосредственно следует, что для его вихрей автоматически справедливым является выполнение знакового принципа. Соответственно, для поля разности фаз можно сформулировать принцип, аналогичный знаковому принципу, которому подчиняются фазовые вихри:

а) на замкнутом -контуре размещается четное количество вихрей поля разности фаз. При этом соседние вихри характеризуются разным знаком топологического заряда (*,~);

b) если соседние вихри разности фаз образованы вихрями фазы одной компоненты, то эти фазовые вихри разных знаков (+,-).

Знак произвольного вихря поля разности фаз фиксирует знаки всех других вихрей. Изменение знака вихря на противоположный автоматически изменяет знаки всех вихрей поля разности фаз.

Расположение - и -контуров можно определить и из других соображений, вытекающих непосредственно из идеи суперпозиции сетей вихрей ортогональных компонент.

Как было показано в п. 2.1, для скалярного случая нули действительной и мнимой частей комплексной амплитуды как функции пространственных координат определяют в плоскости наблюдения два множества непрерывных кривых (линий 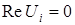, , ). Пересечение этих линий задают сеть вихрей поля. Тогда, в векторном случае для комплексных амплитуд ортогональных компонент поля , 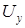имеем две сети фазовых вихрей.

На рис. 3.9 a приведена суперпозиция таких сетей. Толстыми и тонкими линиями обозначены сети вихрей - и 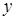-компонент соответственно. Сплошные и пунктирные с крестиком линии (линии 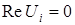, ) определяют множество точек, где действительная и мнимая части комплексных амплитуд ортогональных компонент равны нулю. Линии 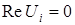, для каждой компоненты электрического вектора разбивают плоскость анализа на области, в которых фаза изменяется в границах 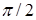(на рис. 3.9 a эти области обозначены римскими цифрами). Именно эти линии и являются эквифазными линиями с фазой, кратной .

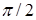Разность фаз комплексных амплитуд ортогональных компонент 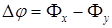=0 может достигаться только там, где накладываются регионы , , , (на рис. 3.9 a эти пересечения отмечены светло-серым цветом), а точки поля с разностью фаз, равной могут находиться только в пересечении областей: , , , . (регионы, обозначенные темно-серым цветом). Аналогично определяются области, в которых может достигаться разность фаз (на рис. 3.9 а такие регионы обозначены белым цветом).

Очевидно, что вследствие непрерывности поля геометрическое место точек, в которых разность фаз комплексных амплитуд ортогональных компонент равняется константе с точностью до , образуют систему замкнутых линий – контуров разности фаз. Лини, вдоль которых разность фаз равняется 0 или , не что иное, как -контуры (на рис. 3.9 a тонкие пунктирные лини), а линии с – -контуры (на рис. 3.9 a тонкие штрихпунктирные линии).

Подчеркнем, что пересечения одноименных линий компонент (пересечения линий и или и ) фиксируют точки поля, в которых разность фаз точно равняется 0 или , т.е. через эти точки проходят -контуры. Пересечения разноименных линий компонент (пересечения линий и или и

) определяют множество точек с разностью фаз , через которые проходят -контуры.

На рис. 3.9 b, - и -контуры также обозначены пунктирными и штрихпунктирными линиями соответственно. Области с левой и правой поляризацией обозначены белым и серым цветом.

Учитывая знаковый принцип и опираясь на факт, что разность фаз вдоль -контура скачком меняется на при переходе через вихрь, можно качественно описать поведение азимута линейной поляризации поля вдоль -контура относительно выбранного базиса разложения поля [28]. Такое поведение вектора поля иллюстрируется на рис. 3.9 b с помощью толстых двойных стрелок.

Проанализируем некоторые особенности сетей, образованных вихрями разности фаз. Отметим, что характеристическая функция зависит от базиса разложения векторного поля на ортогональные компоненты. Соответственно, сеть вихрей разности фаз зависит от выбора ориентации базиса (см. рис. 3.10). Вместе с тем, положение -контуров стационарно и постоянно для произвольного базиса разложения. Простая штрихпунктирная линия и более светлые вихри соответствуют начальному базису разложения. Штрихпунктирная линия с двумя точками соответствует измененному базису. Местоположение -точек обозначено литерой . Для произвольного базиса -контура проходят через эти точки. -контуры, отвечающие двум различным базисам разложения, приведены на рис. 3.9 и обозначены с помощью штрихпунктирной и штрихпунктирной с двумя точками линиями соответственно.

При изменении ориентации базиса могут образовываться новые пересечения - и -контуров, т.е. появляться дополнительные вихри разности фаз.

Естественно, что количество таких вихрей всегда четно, а знаки топологических зарядов подчиняются знаковому принципу.

Проанализируем второе следствие, вытекающее из свойств характеристической функции . Допустим, что комплексная амплитуда скалярного поля изменяется на некоторый постоянный для всего поля фазовый множитель . Векторное поле, соответствующее такому изменению характеристической функции, можно получить, например, размещая на пути распространения волны объект, аналогичный четверть волновой пластинке. При этом структура разности фаз не изменится, но - и -контуры сместятся в соответствии с 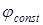. Очевидно, если , - и -контуры поменяются местами.

Таким образом, можно считать, что новая система сингулярностей векторного поля сети вихрей разности фаз сформирована и установлены ее основные свойства.

В последующих параграфах сделаем попытку установить связь между такой системой сингулярностей и дисклинациями, поляризационными сингулярностями.

3.3.3. Вихри ортогонально-поляризованных компонент. Методы исследования поляризационных сингулярностей

3.3.3.1. Вихри ортогональных линейно поляризованных компонент и дисклинации. Экспериментальное определение характеристик -контуров

Рассмотрим некоторую область поля, ограниченную -контуром.

Представим как суперпозицию лево- и правополяризованных циркулярных компонент [3,81]. Из соотношений (3.3) следует, что

, (3.19 a)

или

. (3.19 b)

Рассмотрим изменение главной фазы вдоль -контура.

Каждая из компонент характеризуется своим распределением фазы. Исходя из того, что -точкам поля можно поставить в соответствие вихри циркулярно поляризованных компонент (см. п. 3.1), можно сделать вывод, что позиции вихрей циркулярно поляризованных компонент находятся в областях векторного поля с разным типом поляризации (правой или левой), т.е. разнесены пространственно. Соответственно разнесены пространственно и регионы, в которых наиболее быстро меняется фаза компонент, поскольку такие регионы тяготеют к вихрям. Исходя из этого можно сделать вывод, что в районе -контуров фазы компонент меняются (хотя бы в статистическом смысле) относительно медленно, т.е. 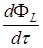производные от фазы компонент вдоль -контура и ( – параметр дуги контура) относительно невелики.

В работе [77] показано, что в точках -контура, где производная от главной фазы , т.е. в точках ее экстремумов, расположены точки рождения и аннигиляции дисклинаций. С другой стороны, как следует из (3.19):

, (3.20 a)

или

. (3.20b)

Соответственно, предполагая, что и 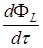невелики, экстремумы азимута поляризации должны наблюдаться в непосредственной близости от точек рождения и аннигиляции дисклинаций. Во всяком случае, вероятность локализации таких точек в области экстремума азимута поляризации значительно выше по сравнению с другими областями -контура.

Дата добавления: 2015-07-12